'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript
The town of Pamiers in the far south of France lies on the Ariège River, north of where it tumbles down from the Pyrenees on its route to join the Garonne (see map in Figure 1b). In modern times the picturesque site has sometimes been an overnight stop in the Tour de France bicycle race. But few visitors would guess that Pamiers, having less than 20,000 people and situated in a rural department, was the town where an important text in the history of mathematics was written nearly six centuries ago.

Figure 1a. The beautiful town of Pamiers, France, in 2000. Some of the buildings here were already standing by the 15th century. (Photograph by M. Bastien, public domain via Wikimedia Commons.)
Swiss scholar Jacques Sesiano, doing research in the French National Library in Paris in the early 1980s, examined and brought to much wider attention the lone surviving copy of an anonymous mathematical text from Pamiers, composed in the Languedocian language originally in the 15th century. Lacking a title, the work is sometimes referred to by an ascribed one, Compendi del Art del Algorisme. It was used as a manual, or handbook, to teach commercial arithmetic to young men preparing for business careers in southern France. It is a good example of the abbaco or algorisme tradition of Medieval and Renaissance times, a type of commercial arithmetic whose instruction and practice had spread through northern Italy and southern France.
One of the striking features of the Pamiers manuscript is the fact that it includes the world’s earliest known instance in which a negative number was accepted as the answer to a problem for purely mathematical reasons. The fact that this occurred in the context of a commercial arithmetic, rather than a more scholastic or theoretical work, is a surprise.
The Pamiers text is similar to many modern textbooks of practical mathematics in one respect: it is filled with story problems. From these, we can get a feel not only for the mathematics of late Medieval and early Renaissance Europe, but also, and especially, for how this mathematics was shaped by commerce and other aspects of culture.
In what follows, I summarize the abbaco tradition of which the Pamiers text was a part, cover some of the arithmetical techniques used in the text, and then present 11 representative story problems from it as a way to explore the mathematical applications that these students were being taught. The 11th problem is the path-breaking one involving negative numbers. I challenge you, the reader, to solve as many of the story problems as you can. You might want to use algebra, matrix methods, or else the purely arithmetical methods covered in the Pamiers text, such as ratio and proportion, inversion (working backward), or false position. Sample solutions are provided in Appendix B.
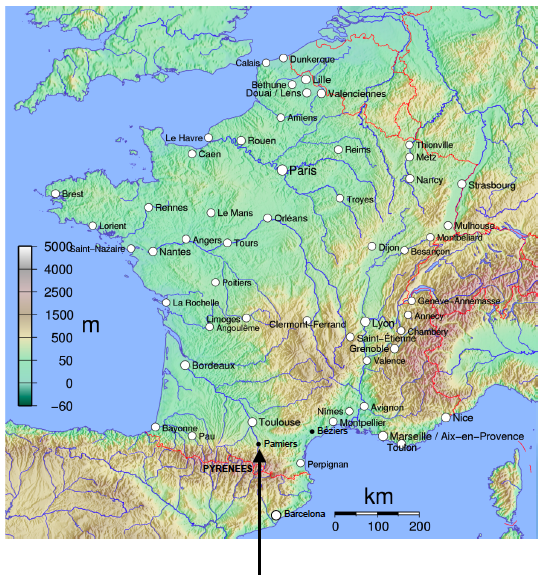
Figure 1b. Map of France with arrow indicating the town of Pamiers. (Image adapted from David Monniaux / Wikimedia Commons.)
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Introduction
The town of Pamiers in the far south of France lies on the Ariège River, north of where it tumbles down from the Pyrenees on its route to join the Garonne (see map in Figure 1b). In modern times the picturesque site has sometimes been an overnight stop in the Tour de France bicycle race. But few visitors would guess that Pamiers, having less than 20,000 people and situated in a rural department, was the town where an important text in the history of mathematics was written nearly six centuries ago.

Figure 1a. The beautiful town of Pamiers, France, in 2000. Some of the buildings here were already standing by the 15th century. (Photograph by M. Bastien, public domain via Wikimedia Commons.)
Swiss scholar Jacques Sesiano, doing research in the French National Library in Paris in the early 1980s, examined and brought to much wider attention the lone surviving copy of an anonymous mathematical text from Pamiers, composed in the Languedocian language originally in the 15th century. Lacking a title, the work is sometimes referred to by an ascribed one, Compendi del Art del Algorisme. It was used as a manual, or handbook, to teach commercial arithmetic to young men preparing for business careers in southern France. It is a good example of the abbaco or algorisme tradition of Medieval and Renaissance times, a type of commercial arithmetic whose instruction and practice had spread through northern Italy and southern France.
One of the striking features of the Pamiers manuscript is the fact that it includes the world’s earliest known instance in which a negative number was accepted as the answer to a problem for purely mathematical reasons. The fact that this occurred in the context of a commercial arithmetic, rather than a more scholastic or theoretical work, is a surprise.
The Pamiers text is similar to many modern textbooks of practical mathematics in one respect: it is filled with story problems. From these, we can get a feel not only for the mathematics of late Medieval and early Renaissance Europe, but also, and especially, for how this mathematics was shaped by commerce and other aspects of culture.
In what follows, I summarize the abbaco tradition of which the Pamiers text was a part, cover some of the arithmetical techniques used in the text, and then present 11 representative story problems from it as a way to explore the mathematical applications that these students were being taught. The 11th problem is the path-breaking one involving negative numbers. I challenge you, the reader, to solve as many of the story problems as you can. You might want to use algebra, matrix methods, or else the purely arithmetical methods covered in the Pamiers text, such as ratio and proportion, inversion (working backward), or false position. Sample solutions are provided in Appendix B.

Figure 1b. Map of France with arrow indicating the town of Pamiers. (Image adapted from David Monniaux / Wikimedia Commons.)
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Background: The Abbaco Tradition
The Pamiers text was designed for use in commercial training schools, which flourished in this part of Europe from the 1200s through the 1500s.
These institutions were known as schools of algorisme (“algorithm”) in French, and of abbaco or abaco in Italian (a word with the general sense of “calculation”). They arose first in northern Italy, whose economy was the most vibrant in Europe during this period (Spiesser 2003, pp. 34-35). A banker and official in Florence, Italy, reported that in 1345 at least 1,000 boys in that city alone were receiving instruction in abbaco and algorismo (Biggs 2009, p. 73). Such schools also began to appear in neighboring southern France, and a few in Catalonia (the area around Barcelona, Spain) and coastal North Africa. These four regions of the western Mediterranean had extensive trade and cultural ties with one another at the time, so it isn’t surprising that they shared methods of practical mathematics and its instruction (Høyrup 2006).
Over 400 of the abbaco and algorisme works have survived. The common ancestor of many of them is Liber Abbaci (1202) by Leonardo Fibonacci of Pisa, Italy. He was only a boy, he reports, when his father, a customs official representing Pisan merchants at their trading enclave of Bugia, in what is now Algeria, brought him to the customs house there to be taught Hindu-Arabic numerals and arithmetic (Sigler 2002, pp. 3, 15). Based on place value, the Arab-style calculations could be carried out on an abacus or with pen and paper, in either case using efficient, step-by-step procedures called algorithms. Fibonacci’s book, written in Latin, introduced this new way of reckoning to European scholars. Then the techniques spread with the aid of texts, like that of Pamiers, that were written in languages more accessible than Latin. Maryvonne Spiesser (University of Toulouse), who has extensively studied the abbaco and algorisme treatises of the region, writes that the Pamiers manuscript “founded the tradition of commercial arithmetics in southern France” (2002, p. 297).

Figure 2. A 19th-century statue of Leonardo Fibonacci in his likely birthplace of Pisa, Italy. The statue, about 15 feet tall, is part of the Fortezza Camp Santo at Giardino Scotto, a fortified garden off a road called Lungarno Fibonacci along the Arno River. (Image made in 2002 by Gordon Wilson, Emeritus Professor of English, Schoolcraft College.)
The boys sent to such abbaco schools were typically 10- to 12-year-olds. Having completed grammar school, they were now training to become merchants, wholesalers, bookkeepers, bankers, or in some cases tax collectors, customs agents, or navigators. Daily instruction was provided by a reckoning master (maestri d’abbaco or maistre d’algorisme); to facilitate his teaching, he would often write his own abbaco text and hire some assistant instructors. The lessons were taught either in the master’s own home or inside a private business, a municipal office, or a religious order. The topics and techniques taught in the abbaco schools were strongly influenced by a tradition that had long thrived within Arab-Islamic culture, that of mu‘āmalāt mathematics, i.e., the mathematics applied to commerce and other aspects of social intercourse. In addition to mathematics, the boys were often given further instruction in reading and writing.

Figure 3. A master teaches his pupils in this drawing from an illuminated manuscript version of Filippo Calandri’s Trattato di Arithmetica, an abbaco treatise originally printed in Florence in 1491. (Source: Biblioteca Riccardiana (Florence, Italy), Ricc. 2669, page 111 verso. Image used by permission; further reproduction is prohibited.)
In general, the abbaco texts offered practical, simplified treatments in which mathematical techniques were distilled into easy-to-remember rules and algorithms. The focus was on how to carry these out rather than on justifying the theory behind them. At the same time, the books were often innovative in their solutions to particular problems and especially in their pedagogical approach: their presentation was popular, and they introduced the use of illustrations and vernacular languages to the history of mathematics textbooks (Swetz 1987, pp. 292-293).
Typically, such a book would give instruction in these topics:
- Arabic place-value numeration and arithmetic, including basic operations with whole numbers and fractions, proportions, progressions, and extraction of roots
- Units of measurement
- Currency exchange
- Metal-alloy and other alligation (mixture) problems
- Computation of costs, revenues, profits, and losses in both barter and money transactions
- Calculations involving partnerships, taxes, and import duties.
Some of the abbaco texts (but not that of Pamiers) included discussions of more advanced or specialized topics, such as these:
- Algebra. An example is Fibonacci’s Liber Abbaci, mentioned above. As the word “algebra” itself attests, this technique was again one that Fibonacci and others had learned from an Arabic context. The hallmark of this approach was to solve a problem by setting up an equation containing a word or symbol for an unknown quantity, and then manipulating the unknown with the same operations as the known quantities. At the time, this was considered a technique that would be fairly difficult for merchants and tradesmen to master.
- Surveying. An example is Fibonacci’s De Practica Geometriae (1220), which showed how to measure and subdivide variously shaped fields as well as solids (see the critical translation by Hughes 2008).
- Marine navigation. An example is the 440-page manuscript book for mariners written by Michael of Rhodes in the Venetian dialect of Italian in the 1430s (see Dibner Institute / WGBH website).
For more on the abbaco and algorisme tradition, see also the works by Biggs, Davis, Goetzmann, Høyrup, and Swetz in the list of References.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - A Synthesis of Mediterranean Methods
The Pamiers text, like other examples of the Medieval algorisme tradition, represented a synthesis of Mediterranean culture, including the commercial practices and mathematical techniques of the region. It is written in Languedocian, an old Romance language of southern France that has now almost disappeared (see Appendix A). Sesiano (1984) provides extensive excerpts from the original Languedocian text, and his own commentary in modern French. (Here on these web pages, all 11 problem statements and other quotations drawn from Sesiano’s redaction have been translated by me from Languedocian into English with the help of a glossary of key terms that Sesiano provides.)
The existing manuscript was handwritten on just over 100 leaves of paper and parchment. It includes no date, title, or author, but it is known to be a copy made in about 1446 of a text originally composed in Pamiers in the 1420s or 1430s, a decade or two before Gutenberg invented his printing press. Copies of books like this had to be made one at a time in the old-fashioned way; special clerks called copyists were employed for this purpose. Spiesser notes that Catholic religious orders, which would have included copyist monks, had a strong presence in Pamiers at the time, and the town also had a university faculty; she speculates that the manuscript’s author might have been a cleric well-versed in the theory and practical techniques of arithmetic (2002, p. 289).
The book opens with benedictions to “our Lord Jesus Christ, merciful and compassionate,” to the Virgin Mary, and to Antonin, patron saint of Pamiers. Then it praises a Muslim scholar from whose name the term algorisme (algorithm) is derived, Muhammad al-Khwārizmī, whom the author described as “a man strongly learned and enlightened, and expert in four sciences [the quadrivium], knowing arithmetic, geometry, music, and astronomy” (Sesiano 1984, pp. 31-32). As inherited from Greek tradition, these were considered the four branches of mathematics when al-Khwārizmī and other scientists flourished in Baghdad around 825 AD.

Figure 4. First page of the Pamiers manuscript. Line 2 of the text begins with an abbreviation for Jesus Christ; line 9 with an underlined name of the town, Pamias (Pamiers); and line 12 with algorisme, which is referred to both as an art and as a real person (i.e., al-Khwārizmī). The markings at the top of the page indicate that the manuscript was once item no. 5194 in the collection of the Bibliothèque de Colbert, and the mark at the bottom identifies it as belonging later to the Bybliothèca Regia (Royal Library). (Image is from Sesiano 1984, p. 30.)
Consistent with its intended use for training in commercial arithmetic, the book consists largely of worked-out examples and story problems, sometimes with little or no justification as to why the methods used are valid. As is true of Medieval works of mathematics in general, no mathematical symbols are used other than the digits for writing numerals.
The manuscript is divided into three sections. The first explains Arabic numerals and the decimal place-value system, then covers the basic arithmetical operations, followed by arithmetic and geometric progressions, and square and cube roots. The second section covers the same topics for fractions, and the third section covers applications of these arithmetical procedures, including roughly 100 story problems.
The pen-and-paper algorithms of arithmetic covered by the Pamiers text were made possible by decimal place-value numeration, which arose in India and then was adapted and advanced by scholars in the Middle East. Many of the algorithms have remained essentially unchanged to this day, while others are somewhat different from those with which we are most familiar. To multiply multi-digit numbers, for example, the Pamiers text recommends the lattice technique, which in Italian is known as multiplication “by gelosia,” a word for the latticed grille on a window. You can probably figure out how the method is carried out by inspecting this example from the manuscript, illustrating the multiplication 437 × 345 = 150765.
.jpg)
.png)
Figure 5. Gelosia (lattice) multiplication (437 x 345) from the Pamiers manuscript. (Image on left is from Sesiano 1984, p. 34.)
The mechanics of this method are shown in a video by PedagoNet, and are explained in Math Forum 1996 as well as Swetz 1987, pp. 80-84, 205-209. The method is also illustrated as part of the solutions to Problem 5 (see Appendix B). Smith (1968, pp. 114-117) notes that lattice multiplication was brought to Italy from the Middle East. The method is still being taught today (see Boag 2007, Nugent 2007).
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Proportionality Techniques
The author of the Pamiers text wrote that his goal in the third and final section was to describe the application of some general rules for “the capable and savvy man to be able to calculate rapidly so as to manage the buying and selling of goods and the forming of companies” (Sesiano 1984, p. 45). The author focuses especially on a handful of algorithms that were widely used in practical settings: the rule of three and methods of false position. These techniques allowed tradesmen to rely on arithmetic alone, in situations that might otherwise have required the use of algebra.
The rule of three is an ancient rote procedure for solving problems involving ratio and proportion. Given three of the four quantities that appear in a standard proportion, the fourth can be calculated using one multiplication and one division. For instance, to cite an example from the Pamiers text (Sesiano 1984, p. 47), “A linen rope that measures 11 and 3/4 cannas in length costs 5 and 2/3 florins, what will one cost that is 5 cannas and 3 and 1/2 pams?,” where 10 pams is 1 canna or about 2 meters. The problem amounts to solving a proportion,
(11 and 3/4) : (5 and 2/3) :: (5 and 7/20) : ?
Those using the rule of three memorized that once the problem was set up in this way, it could be solved by multiplying the two middle terms and dividing the result by the initial term. Doing so here, we get:
(5 and 7/20) × (5 and 2/3) ÷ (11 and 3/4) = 2 and 409/705, or about 2 and 3/5 florins.
The rule of three is discussed further in the Dibner Institute / WGBH website under Toolkit; Goetzmann 2005, pp. 130-132; and Swetz 1987, pp. 101-134, 224-232, 241-242. It is also illustrated as part of the solutions to Problems 1, 5, and 6 (see Appendix B).
In many problem situations, two or more ratios have to be “composed,” also called “compounded.” A typical situation is that of currency conversion. To take a simple example from U.S. experience: if 5 pennies are worth 1 nickel, and 5 nickels are worth one quarter, and 4 quarters are worth 1 dollar, how many pennies are worth 3 dollars? This amounts to solving a proportion,
1 dollar : 100 pennies :: 3 dollars: ?.
In our modern way of thinking, we might treat the ratios as fractions, and multiply them by one another in chainlike fashion, using the units as a guide: \[{\frac{5\,\,{\rm pennies}}{1\,\,{\rm nickel}}}\times{\frac{5\,\,{\rm nickels}}{1\,\,{\rm quarter}}}\times{\frac{4\,\,{\rm quarters}}{1\,\,{\rm dollar}}}\times 3\,\,{\rm dollars}=300\,\,{\rm pennies.}\]
In Medieval times, however, ratios were not thought of as fractions. Instead, such a proportion was solved by an extension of the rule of three, known as the composite rule of three. The pairs of numbers (called antecedents and consequents) from the given ratios were placed alternately on the upper or lower of two rows, laid out successively from left to right:
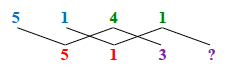
Figure 6.
Practitioners of this rule memorized that one then multiplies the antecedents and divides by the consequents, as guided by the zigzag lines in Figure 6:
(5 × 5 × 4 × 3) ÷ (1 × 1 × 1) = 300.
As employed by money changers, this procedure was known as the “chain rule,” and just as with a real chain it could be continued indefinitely for whatever number of ratios needed to be composed. For more details, see Hughes 2008, pp. 57-59, 99-100; Sigler 2002, pp. 179-211; or Smith 1968, pp. 572-573. The chain rule is also illustrated as part of the solutions to Problem 5 in Appendix B (page 13).
Methods of false position were used for solving problems involving linear relationships. A guess or supposition is made as to the value of the unknown, and based on the degree to which the outcome is “false” (i.e., different from the target value), the supposed value is adjusted to the true position, i.e., the correct answer.
Specifically, problems involving a relationship of the form \(ax = b\) could be solved by single false position. (This makes sense graphically, since a line through the origin is determined by a single additional point.) An input number \(x^{\prime}\) was guessed as the value of the unknown quantity, \(x,\) and the resulting output value \(ax^{\prime} = b^{\prime}\) was found. The resulting proportion, \(b^{\prime}:b\,\,::\,\,x^{\prime}:\,?,\) was then solved by the rule of three. The method is illustrated as part of the solutions to Problems 9 and 10 (see Appendix B).
Problems involving a relationship of the form \(ax + b = c\) could be solved by the rule of double false position. (This, too, makes sense graphically, since an arbitrary line is determined by two distinct points; the method amounts to linear interpolation or extrapolation.) The author of the Pamiers text wrote that the technique is
quite marvelous, finding the truth from two falsehoods. […] We will give several examples and several further instructions that in diverse ways assist in doing various quite difficult calculations, which would without the rule be most fatiguing. (Sesiano 1984, p. 54)
The rule of double false position had been borrowed from the Arab world and introduced to Europe by scholars such as Fibonacci. The latter called it the rule of elchataym, his transliteration of the Arabic name al-khata’ayn, “two falsehoods,” and he devoted Chapter 13 of his Liber Abbaci to it (Sigler 2002, pp. 447-487). Details of the technique can be found in the Dibner Institute / WGBH website under Toolkit; in Schwartz 2010; or in Schwartz 2011. The method is also illustrated as part of the solutions to Problems 1, 3, 4, 7, and 8 (see Appendix B).
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Barter Transactions
A prime example of a type of business transaction that required facility with ratio and proportion is barter, the direct exchange of goods or services. Barter was still common in Europe in the late Middle Ages; one reason is that prior to the European encounter with the New World in 1492, precious metals (and therefore coins) were relatively scarce. The whole ninth chapter of Fibonacci’s Liber Abbaci was devoted to “barter of merchandise and similar things.”
At the same time, barter was beginning to coexist with systems of money that were becoming more common. A sign that barter had entered a new stage was that many barter transactions were being carried out on the basis of rendering the goods’ values in a common monetary unit: this many coins worth of wheat, that many coins worth of oats, etc. A barter was often recorded as such in a register or account book, as if actual coins had been exchanged, when in fact no coins at all were involved.
Because coins were still scarce, the widespread custom among merchants was to set the barter price for a commodity by “marking up” the cash price by a certain percentage. The two barterers had to agree on the markup rate ahead of time, or else one would feel cheated. This type of barter calculation is seen in the following problem drawn from the Pamiers manuscript.

Figure 7. Two merchants negotiate terms to barter wool for cloth in this drawing from an illuminated manuscript version of Filippo Calandri’s Trattato di Arithmetica, an abbaco treatise with many problems similar to those of the Pamiers manuscript. It was originally printed in Florence in 1491. (Source: Biblioteca Riccardiana (Florence, Italy), Ricc. 2669, page 66 recto. Image used by permission; further reproduction is prohibited.)
Problem 1. Two merchants want to barter together, planning to exchange their merchandise; and the first of them has wool and the other has cloth. The one who has cloth wants 24 sous for trading each bolt of cloth whose cash price is but 20 sous. I ask for how much the other must sell each quintal of wool that is worth but 12 liras, in order that he lose nothing. (Sesiano 1984, p. 57)
In order that the second trader “lose nothing,” he must augment his price of 12 liras by the same proportional amount that the first trader has augmented his price of 20 sous to become 24. Thus, the problem amounts to a simple question of ratio and proportion. The author of the manuscript showed how to solve it in two different ways, using the rule of three and double false position, respectively.
Solutions to Problem 1 by proportion (rule of three) and by double false position
Notice that in the above problem, different trade goods were measured with different units: the cloth was measured in bolts, whereas raw wool (as well as other animal hides and many other types of commodities) was measured in quintals, i.e., hundredweights. Even worse, in Medieval times linen might be measured out with different units than other types of woven cloth; grains with different units than other types of food; etc. Expressing all commodity values in some common unit of currency, such as the sous or lira, helped bring some order amid the anarchy of physical units. In fact, this was one of the reasons for the adoption of systems of currency.
In the system of coins that had existed in France since the rule of Charlemagne in the 9th century, 20 sols or sous (from Latin solidus) were equal to one lira or livre (from Latin libra), literally a pound of silver. In English, the sol or sous became the shilling, and the lira or livre became the pound; this is why the British pound was always abbreviated £ for livre.
The Arte dell’Abbaco, an anonymous abbaco text published in the Venetian dialect in 1478, includes a virtually identical problem (see Swetz 1987, p. 152). Like the one above, the problem involves two merchants bartering wool for cloth, with the terms reckoned in soldi; only the numbers are different. Arte dell’Abbaco, the oldest known mathematics book printed in Europe, is often called the Treviso Arithmetic because it was printed in Treviso, just inland from Venice, Italy.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Currency Exchange
The regional economies that existed in Europe, or even within a single realm such as France, still hadn’t become well integrated in these pre-modern times, and in general, there were no standardized monies backed by strong governments. Thus, like most Medieval and Renaissance arithmetic texts, the Pamiers manuscript includes many problems dealing with conversions between local currencies.
The practice of minting coins of silver, gold, and other precious metals had arisen many centuries earlier. However, each region tended to have its own coins. Weights and measures also varied from place to place, and even in a given location different units were used for different commodities, as we saw earlier in Section 5 on Barter Transactions. The confusing proliferation of local currencies, weights, and measures in France wasn’t swept away and replaced with a rational, unified, nationwide system until the Revolution of 1789.

Figure 8. “The Moneylender and His Wife” (1514) by Flemish painter Quentin Matsys. Musée du Louvre, Paris. (Image: The Yorck Project / Wikimedia Commons, licensed under the GNU Free Documentation License.)
Many problems of currency conversion, such as the following one from the Pamiers manuscript, are of the type that can be solved by the use of ratio and proportion.
Problem 2. If 3 deniers of Perpignan are worth 5 deniers of Montpellier, and 2 of Montpellier are worth 3 of those of Avignon, I ask how many of those of Perpignan are worth 12 of those of Avignon. (Sesiano 1984, p. 49)
In the above problem there is a twist, because more than just one ratio is given. But this was actually routine for money changers: typically, they knew the exchange rates for neighboring currencies, but to exchange more-distant currencies they had to build a chain out of such pairs of neighbors. Indeed, Perpignan, Montpellier, and Avignon are 3 cities strung along the Mediterranean coast in the order mentioned in the above problem, across a distance of roughly 150 miles, providing a nice geographical interpretation for the concept of “chain.” See if you can solve the problem by one of the methods discussed in Section 4.
Solutions to Problem 2 using composite rule of three, using chain rule, and using algebra
It’s also interesting to note that the term denier mentioned in the above problem goes back to the time of King Charlemagne, who instituted a system of coins, weights, and measures around 800. The term is based on the Latin denarius, an ancient Roman silver coin that had ten times the value of an as, a coin of copper or bronze; the Latin root for “ten” is seen in denarius, as also in English words like decimal and dime. After the Norman conquest of England (1066), Charlemagne’s system of monetary units made its way across the Channel, where the silver denier eventually became known as the penny (plural pennies or pence); this is why the British penny was formerly always abbreviated “d” for denier. In turn, 12 deniers were equal to one sous, a coin mentioned earlier in Section 5 on Barter Transactions.
Monetary questions—including currency exchange, the money supply, and the alloying of precious metals—were complex enough that European mathematicians would sometimes advise rulers on this subject and write treatises about it. The entire Chapter 11 of Fibonacci’s Liber Abaci (1202) is concerned with “the alloying of monies.” Another prime example of this tradition is Nicole d'Oresme (1323-1382), a mathematician and religious philosopher of Norman origin who became both the chaplain and monetary advisor to French King Charles V. By 1355, Oresme had written an important treatise about money, De Origine, Natura, Jure et Mutationibus Monetarum. Paper money did not come into use in England until the 1690s, and in France not until the 1700s.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Prices and Purchases
Each of our next two sample problems entails a set of purchases that can be analyzed as a system of linear relationships.
The first is stated in terms of the sous, a coin mentioned earlier, and the setier, a measure of volume for liquids and grains that is roughly two gallons (it was one of the units swept away by the French Revolution). See whether you can figure it out.
Problem 3. A merchant paid 10 liras, which is 200 sous, for two manners of grain, namely wheat and oats, and he purchased each setier of wheat for 10 sous and each setier of oats for 5 sous. This merchant turned around and sold his grain, selling each setier of oats for 4 sous and each setier of wheat for 12 sous, and realized a profit of 10 sous. I ask how many setiers of wheat and how many of oats he purchased, and how much money he paid for each grain. (Sesiano 1984, p. 56)
The other sample problem mentions a gold coin of France called a “lamb of gold” (moto d’aur in Languedocian or mouton d’or in modern French, cognate with the English word “mutton”). It was worth 12½ sous. The coin contained an image of a lamb accompanied by a Latin inscription to Christ, who is often referred to by Christians as Agnus Dei, the Lamb of God. See the photograph of a moto (a moto photo!) below.

Figure 9. A “lamb of gold” coin from France, this one struck in the year 1311. Abbreviated in Latin is an invocation to Christ, Agnus dei qui tollit peccata mundi miserere nobis (“Lamb of God who bears the sins of the world, take pity on us”). (Image: Classical Numismatic Group, Inc. / Wikimedia Commons, licensed under the GNU Free Documentation License.)
Problem 4. A merchant purchased three pieces of cloth that cost him [a total of] 30 motos, and doesn’t know with certainty what each of the pieces cost, but does know that the second cost double the first and 4 more; the third cost three times as much as the second, less 7. I ask what each one cost. (Sesiano 1984, p. 55)
Solutions to Problem 4 by double false position and by algebra
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - First Shoots of Capitalism
Many of the story problems in the Pamiers text reflect the emergence of the company (companhia in Languedocian), a partnership of men banded together in an ongoing money-making enterprise.
Typically these entrepreneurs were already wealthy men, such as successful merchants. They would each advance some of their own money to help establish the company, in hopes that it would later gain additional money or profit (called in Languedocian gasanh, literally “gain” or “winnings”).
One of the key types was the “company of limited duration,” where merchants invested varying amounts of money and time in the enterprise. As exemplified by the problem below, the profit was divided, or parceled out, to each investor in proportion both to the money that he’d advanced and to the time that he’d waited before getting his return.

Figure 10. Three business partners divide their proceeds in this drawing from an illuminated manuscript version of Filippo Calandri’s Trattato di Arithmetica, an abbaco treatise with many problems similar to those of the Pamiers manuscript. It was originally printed in Florence in 1491. (Source: Biblioteca Riccardiana (Florence, Italy), Ricc. 2669, page 64 recto. Image used by permission; further reproduction is prohibited.)
Problem 5. Three merchants formed a company together. The first advanced 200 motos and stayed for 15 months, the second advanced 94 motos and stayed for 17 months, the third advanced 38 motos and stayed for 10 months; and at the end they realized a profit of 400 [motos]. I ask how it should be divided [among them]. (Sesiano 1984, p. 47)
Just like today, to have one’s money tied up in an investment for a period of time was seen as an imposition, and the burden was proportional both to the amount of money and the amount of time. Time and money alike were quantities that should redound to the person who ventured to invest them. Thus, in the above problem, the shares of profit need to be reckoned based on the product of each merchant’s time and money. The Treviso Arithmetic, a book mentioned in Section 5, Barter Transactions, contains two problems very similar to this one (see Swetz 1987, pp. 138-151, 236-238).
Solution to Problem 5 by proportion and gelosia multiplication
The formation of such companies was clearly an embryonic shoot of capitalism, a stage of society that emerged in late Medieval times in Italy and then also coalesced in neighboring countries. The characteristic feature of capitalism is that goods and services are produced not for their intrinsic value but for their usefulness in making money. In a capitalist enterprise, the profits made are more important than the products made; that is why in story problems like the one above, the nature of the company is not mentioned.
The most powerful early capitalists were merchants, like those mentioned in the preceding three story problems. But the dominance of merchants was eventually replaced by that of factory owners and then bankers. Our words factory and manufacture arose because French and Italians referred to a craftsman as a factor, as seen in the next problem. Factor was originally a Latin term for “doer,” “maker,” “producer.” In other words, factors made a product. This terminology is also seen in mathematics more directly: for example, the factors 2 and 3 make the product 6.
In manufacturing, a common type of association that arose at this time was the commande or commenda contract, in which merchants invested capital only, whereas factors invested their labor and possibly some capital as well. The money value of the craftsman’s labor, agreed upon ahead of time, would play a key role when it came time to divide the profits or losses— even if things didn’t go as planned, as was the case in this next problem.
Problem 6. A merchant gave 600 liras to a factor who had 200 liras of his own, by such arrangement that he work with that 800 liras for 5 years, and at the end of that time [said the merchant] we will divide in half the principal and the profit. It so happened that the factor spent none of the 200 liras, but had made use of the 600 liras of the merchant; and at the end of 5 years had realized 2400 liras, counting principal and profit. I ask how the division should be carried out— considering that the factor spent none of what he should have spent— in order that the merchant not be deceived. (Sesiano 1984, p. 48)
One can imagine various ways to resolve this problem, but in the real world it was solved by a strictly proportional division of the proceeds. For five years, the merchant had no access to any of the money he’d invested, whereas the factor was free to use his 200 liras in any way he liked. Thus, “in order that the merchant not be deceived,” it should be reckoned that in this case, the factor’s only investment was the value of his labor. (Hint: first determine the agreed-upon value of the factor’s five years of labor, in liras.)
Solution to Problem 6 by proportion
The above problem suggests that from the earliest days of capitalism, whenever labor and capital came together to produce things, there were issues of judgment, law, ethics, and potential conflict that were involved. First, the value of labor, in liras or other monetary units, had to be negotiated ahead of time. Second, all sorts of unexpected things could happen before the goods were produced and sold.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - A Fair Was Serious Business
To us, fairs are pretty much just amusements. But in Europe during the Middle Ages and Renaissance, they were serious business affairs— the major engines of economic growth.
Most towns had had a market day since ancient times— a certain day of the week set aside for buying and selling produce and other goods. But in the 1100s, the most ambitious cities in Europe began to host annual international trade fairs lasting one to three weeks, often coinciding with holy days and pilgrimages. These fairs drew buyers and sellers— in both cases mostly merchants and middlemen— from much greater distances than a market day: at a single fair, merchants from Italy, France, and the Low Countries might be found selling their wares. The most important commodities were fabrics. They ranged from coarser cloths of flax or wool to fine woven silks, a specialty of Lyon in southern France. The Lyon Fair was established by Charles VII in 1420, only a few years or so before the Pamiers text was written.

Figure 11. The lower floor of a restored medieval fondaco in Provins, northern France, which was rented by merchants and craftsmen during an annual international fair. Beginning in the 1100s, the annual fairs held in Provins and five other towns in the Champagne and Brie regions helped circulate textiles, spices, and other fine goods between northern Italy, Catalonia, and southern France, on the one hand, and northern Europe on the other. A fondaco was a combination of an inn, warehouse, and factory. (Image: Provins Office of Tourism.)
These fairs became a central feature of the economy of late Medieval and early Renaissance Europe, driving social development as a whole:
- To protect the merchants and their stalls of goods that were set up in the streets, rulers organized forces of fair wardens with the power to arrest and try wrongdoers, and these evolved into the police forces and courts of European cities.
- Special “King’s Roads” were built to convey merchants and merchandise safely and efficiently to the host cities, and these became the major thoroughfares of the region.
- Lodgings for out-of-town buyers and sellers, and storehouses for their wares, evolved into hostelries, warehouses, and factories.
- Merchants arriving from other countries hired advocates to argue for their interests, and these developed into foreign consulates.
- Cities and governments grew bigger and wealthier by hosting fairs and then levying entry and exit tolls, sales taxes, and fees for weighings and measurings.
- Loans, credit purchases, and “bills and letters of exchange” were invented so that merchants could raise the capital needed to pay craftsmen for their feverish work during the months leading up to a fair.
- Exchange between foreign currencies at major fairs became so important that it sparked the ascendance of banking and finance over trade and manufacturing.
To read more about the fairs of Europe, see (Verlinden 1963, pp. 119-153).
In the following problem, two merchants arriving at a fair with some raw wool are charged a duty, or import tax, at some set rate that we aren’t told. The collected duties would be forwarded to the local or national government, helping to enrich them.
Problem 7. Two merchants went to the fair; the first had 20 sacks of wool, for which he paid the duty collector 1 sack of the wool, and the collector returned to him 2 liras; the second had 60 sacks of wool, for which he paid the collector 2 sacks of wool plus 6 liras. I ask the value of each sack of the wool, and how much was paid the collector per sack. (Sesiano 1984, p. 56)
Note that the duties, and any “change” returned, could be paid either with liras or with wool itself. There are two unknowns that are requested, which can be found from the two linear relationships that are involved.
Solutions to Problem 7 by double false position and by algebra
Fibonacci’s Liber Abbaci, mentioned earlier, included three consecutive maritime import problems very similar to the fair problem above. Instead of duties on wool in liras, these involve, respectively, freight charges on wool in soldi, customs on precious stones in bezants, and customs on fish in denari (see Sigler 2002, pp. 395-397).
The poor fellow in the next problem is a disgrace to the merchandising profession, since he is spending money almost as fast as he is earning it!
Problem 8. A man entered a fair, and the first day doubled all his money and spent 1 gros; likewise on the second tripled all his money that he had left and spent 2 gros; likewise on the third quadrupled his money that he had left and spent 2 gros, and found that he had nothing but 3 gros. I ask how much money he carried [to the fair]. (Sesiano 1984, p. 58)
The author of the manuscript showed how to solve this problem by double false position. Of course, it can also be solved by inversion (“working backward”) or by algebra.
Solutions to Problem 8 by double false position, by inversion ("working backward"), and by algebra
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - A Source of the Two-Trains Problem?
As with a modern textbook, the Pamiers text contains a number of story problems that, while challenging, are of dubious practical value. They are contrived examples dressed up as real-world applications. The real purpose of these “recreational” puzzles is to further sharpen the mathematical skills of the students.
Among the examples given in the Pamiers text are several that remind us of classic problems still found in modern textbooks. Consider the following rate-and-time problem.

Figure 12. A wine cask with three taps, one bigger than the other two, appears in this drawing from an illuminated manuscript version of Filippo Calandri’s Trattato di Arithmetica, an abbaco treatise with many problems similar to those of the Pamiers manuscript. It was originally printed in Florence in 1491. (Source: Biblioteca Riccardiana (Florence, Italy), Ricc. 2669, page 108 verso. Image used by permission; further reproduction is prohibited.)
Problem 9. A cask [of wine] has three taps, the first bigger than the others, and in such a manner that with the biggest open, all the wine empties in 3 hours; and with the medium one open, it empties in 4 hours; and with the smallest open, it empties in 6 hours. I ask when all the taps are open together, in how much time will the wine empty. (Sesiano 1984, pp. 53-54)
We are given to assume that the draining speed of each tap is constant over time.
Solutions to Problem 9 by single false position and by addition of rates
In its modern form, such a problem might be phrased: “Michael can mow the entire lawn in 3 hours, Ellen in 4 hours, and Art in 6 hours….” Although the story is different, the mathematics is exactly the same! This suggests that some types of problems are old standards that have persisted for centuries, their form gradually evolving over time (see Sanford 1972). In fact, more than 200 years earlier, in Chapter 12 of Fibonacci’s Liber Abaci, we find almost this same example, but instead of “three spigots,” the vat has “four holes at the bottom” (Sigler 2002, p. 281).
The following problem, although nearly six centuries old, is highly reminiscent of a modern classic: “Two trains leave their stations in Detroit and Chicago at the same time…,” but instead of waving to each other from passing trains, the two men involved see each other on horseback.
Problem 10. Two men leave on the same day and the same hour from two cities, say for example the first leaves Béziers for Barcelona and the other goes from Barcelona to Béziers. And the one that leaves Béziers does the route in 7 days, and the other takes 9 days. I ask how much time is required before they see each other, and [if the cities are separated by 63 leagues] how far each has traveled. (Sesiano 1984, p. 54)
We are given to assume that the speeds of both men are constant over time. And if you think about it, Problem 10 is mathematically of the same type as Problem 9: instead of three taps working together to drain an entire wine cask, two men are working together to cover an entire distance of 63 leagues.
Solutions to Problem 10 by single false position, by addition of rates, and by algebra
The Treviso Arithmetic contains an almost identical problem (see Swetz 1987, pp. 158-160). The men are couriers sent between Rome and Venice, a distance of 250 Roman miles, but the travel times are still 7 and 9 days.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Acceptance of Negative Solutions

Figure 13. Pieces of fine cloth are being sold in this scene from one of the annual international Fairs of Champagne in medieval northern France. The engraving is from a 19th-century book. (Image: Wikimedia Commons.)
The Pamiers manuscript also includes recreational problems in which a group of men consider pooling their money to buy an expensive item, such as a horse or a piece of fine cloth. Each man tells the others what fraction of their money they would need to give him in order for him to afford the purchase.
Problem 11. There are 5 men who [each] want to purchase a piece of cloth in such manner [i.e., at such a cost] that the first asks of all the others 1/2 of all the gold and silver they carry, the second asks 1/3, the third asks 1/4, the fourth [asks] 1/5 and the fifth asks 1/6. I ask what the piece cost and what each of them carried. (Sesiano 1984, p. 52)
In this rather contrived problem, which involves a series of linear relationships, no actual monetary amount is specified. As in all such problems, it turns out that what matters is only the ratios among the unknowns. Thus, there are infinitely many solutions, but all of them are multiples of one another. The author used a rote procedure to find the solutions, but supplied no justification for the procedure.
This genre of problem, despite its complexity, was already very old by the 1400s. Fibonacci, for example, had solved quite a few of these in Chapters 12 and 13 of his Liber Abbaci; they always involve a group of men in a commercial situation, such as chancing upon a purse with money, or pooling their money to buy a horse, etc. Going back further, this type of problem is also found in treatises from the Middle East in the 10th century, and even older Chinese and Byzantine works (Sesiano 1985, p. 112).
What makes the discussion in the Pamiers text exceptional, even within this centuries-old tradition, is the fact that in the case of the above problem, one quantity turns out to be negative in each solution, and the author accepts this as completely legitimate without further comment. He derives his result without making a fuss about the negative quantity, which he records matter-of-factly as 10 et ¾ mens de non res (“10¾ less than nothing”). Unlike Fibonacci, he makes no attempt to interpret what it would mean for a man to pool his “negative” gold and silver with that of his companions in order to afford a piece of cloth. Clearly, in this instance at least, the anonymous author was more interested in the mathematics itself than in its practical application. In the whole of world history, this is the earliest known instance in which a negative final answer—not just a negative intermediate result—was accepted for purely mathematical reasons, i.e., because it satisfied the constraints of the problem (Sesiano 1984, pp. 28, 51-53; Sesiano 1985, pp. 133-134, 148).
The receptivity of the text’s author to the concept of negative numbers also seems to underlie his highly unusual, but quite perceptive, characterization of subtraction as the opposite of addition (sostrayre es lo contrari de aiustar, Sesiano 1984, p. 32), and similarly of division as the opposite of multiplication. This realization would not have been feasible without a full acceptance of negatives (Spiesser 2002, p. 290-291).
The new attitude toward negative quantities was one that had to swim against the prevailing tide of mathematical practice—but ultimately it won out, marking a turning point in the history of mathematics. Some of the first southern-French algorisme texts written after the appearance of that of Pamiers would copy verbatim many of the latter’s problems of this genre, while omitting this particular problem, apparently a sign of their authors’ reluctance to accept negative solutions (Spiesser 2002, p. 297). However, by the end of the century, such solutions had been accepted in at least five other treatises, most of which came to be far better known than the Pamiers work:
- Lo Compendion de lo Abaco (probably c. 1460), written by Francès Pellos in the Niçois dialect of the Occitan language. Later, in the year 1492, this work would be published in Turin, the first book—of any kind—printed in Niçois. (Sesiano 1985, p. 134)
- The Compendy de la Praticque des Nombres (probably c. 1471), an abbaco manuscript written in French by a Dominican friar in southern France, Barthélemy de Romans. His negative numbers arose in the same type of problems discussed by others (horse purchases, etc.), and he used the same term “less than nothing” (meins de riens) as had been used in the Pamiers manuscript. (Spiesser 2004)
- The Tractatus Mathematicus ad Discipulos Perusinos (1478), a commercial arithmetic that Luca Pacioli wrote in Italian for his students at the University of Perugia. (Sesiano 1985, pp. 142-146)
- The Triparty en la Science des Nombres (1484), written in French by Nicolas Chuquet in Lyon, which included negative solutions for a wider range of story problems and also for some abstract problems. (Sesiano 1985, pp. 134-142)
- Pacioli’s Summa de Arithmetica, Geometria, Proportioni et Proportionalità (1494), a textbook in Latin published in Venice. (Sesiano 1985, pp. 146-147)
Of course, the eventual acceptance of negative numbers was inevitable, and their use would prove to be of immense importance in mathematics. It furthered techniques that are needed to solve many of the more advanced practical problems, and it led to a great expansion in the scope of mathematical theory. We can see this impact in such topics as the algebraic solution of polynomial equations, in the now-ubiquitous use of complex numbers, and in notions of identity, inverse, and algebraic structure.
The Pamiers text helps us see that European mathematics advanced to new heights because of constant interaction between its theory and its practical applications, and also because of the rich interaction among many different peoples, cultures, and practices, not all of them native to Europe.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Appendix A: The Land of 'Oc'
The mathematical text described in this article was written in Languedocian, one of a whole family of Romance languages once spoken in southern France. It’s amazing to learn what a variety of tongues could be heard in the recent past, both in the south and in the north of the country.
The peoples of France since the early Middle Ages generally fell into two groups: those of the south, whose word for “yes” was òc, and those of the north, whose word for “yes” was oïl. The latter evolved into the oui of modern French. The term Languedocian derives from the phrase langue d’Òc, meaning “language of Òc.”
Other languages or dialects in this family included Provençal, Niçois, Piemontese, and several more. They were spoken in southern France and in parts of Italy and Spain. Not surprisingly, these languages are more recognizably similar to modern Italian than are those of the north. Some of the greatest literature of the Middle Ages was created in this region by troubadours, the lyric poets who recounted tales in story and song. The word troubadour itself is from the Provençal for “one who finds or invents.”
Language is such an important marker of cultural identity that over time, Languedoc came to mean not only the language family itself, but also all of the French lands where it was spoken. Today, the language family is referred to instead as Occitan.
Today in France, visitors have a hard time finding traces of dialects other than standard Parisian. This reflects the growing political unification of the country after the 1789 Revolution. At that time, there were only about 3 million people who could speak what is now called French. The area around Avignon in the south was absorbed into the country only in 1791, while the city of Nice (homeland of the Niçois language) was ceded to France by Sardinia only in 1860. In 1881, the French prime minister ordered that schoolchildren be punished if they spoke Occitan or other regional languages! By 1893, only about one-quarter of the French population of 30 million didn’t speak the designated official language (Weber 1991, p. 95). The Occitan languages almost became extinct— another sign of a sharp loss of linguistic diversity all over the world because of the impact of modernization and globalization.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Appendix B: Solutions
Below, we have provided at least one solution to each of the 11 problems selected from the Pamiers text. Other methods of solution may be possible.
Problem 1. Two merchants want to barter together, planning to exchange their merchandise; and the first of them has wool and the other has cloth. The one who has cloth wants 24 sous for trading each bolt of cloth whose cash price is but 20 sous. I ask for how much the other must sell each quintal of wool that is worth but 12 liras, in order that he lose nothing.
The author of the Pamiers manuscript showed solutions similar to B and C below.
Solution A: a proportion using the augmented (“marked-up”) selling prices
Begin with the proportion,
20 sous : 24 sous :: 12 liras : ?
(This is like asking, “A marked-up price of 24 sous on a list price of 20 sous is equivalent to a marked-up price of how many liras on a list price of 12 liras?)
By the rule of three, the marked-up price is therefore (12 × 24) ÷ 20 = 288 ÷ 20 = 14 2/5 liras, or 14 liras 8 sous.
Solution B: a proportion using the markups
Begin with the proportion,
20 sous : 4 sous :: 12 liras : ?
(This is like asking, “A markup of 4 sous on a list price of 20 sous is equivalent to a markup of how many liras on a list price of 12 liras?)
By the rule of three, the markup is therefore (12 × 4) ÷ 20 = 48 ÷ 20 = 2 2/5 liras, or 2 liras 8 sous.
Augmenting the price of 12 liras by the markup of 2 liras 8 sous gives a marked-up price of 14 liras 8 sous.
Solution C: double false position using the markups
Begin with the proportion,
20 sous : 4 sous :: 12 liras : ?
Note 12 × 4 = 48.
First, suppose the markup is 2 liras. But 20 × 2 = 40, a deficit of 8.
Second, suppose the markup is 3 liras. But 20 × 3 = 60, an excess of 12.
By double false position, the correct markup is therefore
\[{\frac{(2\times12\,{\rm excess})+(3\times8\,{\rm deficit})}{12\,{\rm excess}\,+8\,{\rm deficit}}}={\frac{48}{20}}\]\[=2\frac{2}{5}\,{liras}=2\,{liras}\,\,8\,{sous}.\]
Augmenting the price of 12 liras by the markup of 2 liras 8 sous gives a marked-up price of 14 liras 8 sous.
Problem 2. If 3 deniers of Perpignan are worth 5 deniers of Montpellier, and 2 of Montpellier are worth 3 of those of Avignon, I ask how many of those of Perpignan are worth 12 of those of Avignon.
The author showed a solution similar to A below.
Solution A: composite rule of three \[\frac{5}{3}\times\frac{3}{2}=\frac{5}{2}\]
5 : 2 :: 12 : ?
(12 × 2) ÷ 5 = 24 ÷ 5 = 4 4/5 deniers.
Solution B: chain rule
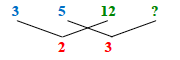
(3 × 2 × 12) ÷ (5 × 3) = 24 ÷ 5 = 4 4/5 deniers.
Solution C: algebra
Given \(3P=5M,\) and \(2M=3A,\) we have \[P={\frac{5}{3}}M,\quad M={\frac{3}{2}}A\] \[P={\frac{5}{3}}\left({\frac{3}{2}}{A}\right) = {\frac{5}{2}}A\] \[{\frac{2}{5}}P=A\] \[12\left({\frac{2}{5}}P\right)=12A\] \[{\frac{24}{5}}P=12A\]
Thus, 24/5 or 4 4/5 deniers of Perpignan are worth 12 of those of Avignon.
Problem 3. A merchant paid 10 liras, which is 200 sous, for two manners of grain, namely wheat and oats, and he purchased each setier of wheat for 10 sous and each setier of oats for 5 sous. This merchant turned around and sold his grain, selling each setier of oats for 4 sous and each setier of wheat for 12 sous, and realized a profit of 10 sous. I ask how many setiers of wheat and how many of oats he purchased, and how much money he paid for each grain.
The author showed a solution similar to A below.
Solution A: double false position
First, suppose he sold 10 setiers of wheat at 10 sous, thus 100 sous total.
Then he paid 200 – 100 = 100 sous for the oats at 5 sous,
and thus purchased 100 ÷ 5 = 20 setiers of oats.
So his sales proceeds are
(10 setiers of wheat at 12 sous) + (20 setiers of oats at 4 sous) = 120 + 80 = 200 sous
and his profits are therefore
200 – 200 = no sous, instead of the stated 10 sous (thus, deficit 10).
Likewise, suppose he sold 15 setiers of wheat. Then we get
200 – 150 = 50
50 ÷ 5 = 10
(15 × 12) + (10 × 4) = 220
and his profits are therefore
220 – 200 = 20 sous, instead of the stated 10 sous (thus, excess 10).
By double false position, the correct amount is thus \[{\frac{(10\,{setiers}\,\times10\,{sous}\,{\rm excess})+{(15\,{setiers}\,\times10\,{sous}\,{\rm deficit})}}{10\,{sous}\,{\rm excess}+10\,{sous}\,{\rm deficit}}}=\frac{250}{20}=12\frac{1}{2}\] setiers of wheat. Therefore, he paid 12 1/2 × 10 = 125 sous for the wheat and 200 – 125 = 75 sous for the oats, and so the quantity of oats purchased was 75 ÷ 5 = 15 setiers.
Check. The proceeds were thus (12 1/2 × 12) + (15 × 4) = 210 sous, a profit of 210 – 200 = 10 sous.
Solution B: algebra (simple elimination)
Let \(x=\) the quantity of wheat, and \(y=\) the quantity of oats. Then \[10x+5y=200\] \[12x+4y=210.\]
Dividing the equations by \(5\) and \(4,\) respectively, we get \[2x+y=40\] \[3x+y=52.5.\]
Subtracting the first equation from the second eliminates the second variable, leaving \[x=12.5,\]
so \(12.5\) setiers of wheat were purchased for \(12.5\times 10=125\) sous.
Back-substituting this result yields \[2(12.5)+y=40\] \[25+y=40\] \[y=15,\]
so \(15\) setiers of oats were purchased for \(15\times 5=75\) sous.
Solution C: matrix algebra
Given \[\left[ {\begin{array}{cc}
10&5 \\
12&4 \\ \end{array}}\right]\left[ {\begin{array}{c}
x\\
y\\ \end{array}}\right]=\left[ {\begin{array}{c}
200\\
210\\ \end{array}}\right],\]
the quantities of wheat and oats purchased were \[\left[ {\begin{array}{c}
x\\
y\\ \end{array}}\right]={{\left[ {\begin{array}{cc}
10&5 \\
12&4 \\ \end{array}}\right]}^{-1}}\left[ {\begin{array}{c}
200\\
210\\ \end{array}}\right]=\left[ {\begin{array}{c}
12.5\\
15\\ \end{array}}\right];\]
that is, 12.5 setiers of wheat and 15 setiers of grain, and so the amounts paid were 10 × 12.5 = 125 sous and 5 × 15 = 75 sous, respectively.
Problem 4. A merchant purchased three pieces of cloth that cost him [a total of] 30 motos, and doesn’t know with certainty what each of the pieces cost, but does know that the second cost double the first and 4 more; the third cost three times as much as the second, less 7. I ask what each one cost.
The author showed a solution similar to A below.
Solution A: double false position
Suppose the first piece cost 3 motos.
Then the second piece cost (2 × 3) + 4 = 10 motos,
and the third piece cost (3 × 10) – 7 = 23 motos.
But 3 + 10 + 23 = 36 motos, an excess of 6.
Suppose the first piece cost 4 motos.
Then the second piece cost (2 × 4) + 4 = 12 motos,
and the third piece cost (3 × 12) – 7 = 29 motos.
But 4 + 12 + 29 = 45 motos, an excess of 15.
By double false position, the true position is thus \[{\frac{(3\times15\,{\rm excess})-{(4\times\,6\,{\rm excess})}}{15\,{\rm excess}-6\,{\rm excess}}}=\frac{21}{9}.\]
Therefore, the first piece cost \(\frac{21}{9}\) or \(2\frac{1}{3}\) motos,
the second piece cost \(\left(2\times2\frac{1}{3}\right)+4=8\frac{2}{3}\) motos,
and the third piece cost \(\left(3\times8\frac{2}{3}\right)-7=19\) motos.
Check. The total cost was thus \(2\frac{1}{3}+8\frac{2}{3}+19=30\) motos.
Solution B: algebra
Let x = the cost of the first piece.
Then the cost of the second piece is 2x + 4,
and the cost of the third piece is 3(2x + 4) – 7.
Since the total cost of the three pieces is 30 motos, we have:
x + (2x + 4) + (3(2x + 4) – 7) = 30.
x + (2x + 4) + (6x + 12 – 7) = 30.
9x + 9 = 30
9x = 21
x = \(\frac{21}{9}\) or \(2\frac{1}{3}\) motos, etc. as in Solution A above.
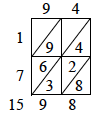
Problem 5. Three merchants formed a company together. The first advanced 200 motos and stayed for 15 months, the second advanced 94 motos and stayed for 17 months, the third advanced 38 motos and stayed for 10 months; and at the end they realized a profit of 400 [motos]. I ask how it should be divided [among them].
Solution by proportion:
200 motos × 15 months = 3000
94 motos × 17 months = 1598
38 motos × 10 months = 380
Total = 4978.
The lattice or gelosia technique proceeds as follows for the second of the three multiplications noted above.
Using the rule of three, the proportional shares of the profit are, respectively,
4978 : 3000 :: 400 : ? implies 400 × 3000 ÷ 4978 = \(241\frac{151}{2489}\) motos
4978 : 1598 :: 400 : ? implies 400 × 1598 ÷ 4978 = \(128\frac{1008}{2489}\) motos
4978 : 380 :: 400 : ? implies 400 × 380 ÷ 4978 = \(30\frac{70}{131}\) motos.
Check. The total profit is thus \(241\frac{151}{2489}+128\frac{1008}{2489}+30\frac{70}{131}=400\) motos.
Problem 6. A merchant gave 600 liras to a factor who had 200 liras of his own, by such arrangement that he work with that 800 liras for 5 years, and at the end of that time [said the merchant] we will divide in half the principal and the profit. It so happened that the factor spent none of the 200 liras, but had made use of the 600 liras of the merchant; and at the end of 5 years had realized 2400 liras, counting principal and profit. I ask how the division should be carried out— considering that the factor spent none of what he should have spent— in order that the merchant not be deceived.
Solution by proportion:
By agreeing in advance to divide their proceeds in half, the two men were valuing equally their prospective contributions: 600 liras from the merchant, and 200 liras plus 5 years of labor from the factor. Therefore, the value of the factor’s five years of labor was 600 – 200 = 400 liras.
The factor’s 200 liras of money that ended up not being needed for production cannot be thought of as part of the investment, since throughout the five years the factor was free to use that money in any way that pleased him. Therefore, the total value invested by the two men together was 600 + 400 = 1000 liras, and the total proceeds on the investment itself were 2400 – 200 = 2200 liras. These 2200 liras must be divided between the two men in proportion to their respective shares in the investment, namely 600 and 400 liras. Using the rule of three,
merchant’s share, 1000 : 600 :: 2200 : ? implies 2200 × 600 ÷ 1000 = 1320 liras
factor’s share, 1000 : 400 :: 2200 : ? implies 2200 × 400 ÷ 1000 = 880 liras.
(The factor also retains his unused 200 liras for a total of 1080 liras.)
Check. The total proceeds were thus 1320 + 880 = 2200 liras.
Problem 7. Two merchants went to the fair; the first had 20 sacks of wool, for which he paid the duty collector 1 sack of the wool, and the collector returned to him 2 liras; the second had 60 sacks of wool, for which he paid the collector 2 sacks of wool plus 6 liras. I ask the value of each sack of the wool, and how much was paid the collector per sack.
The author showed a solution similar to A below.
Solution A: double false position
First, suppose the value of each sack is 4 liras.
Then the tax on 20 sacks, being 1 sack minus 2 liras, is 4 – 2 = 2 liras.
Thus, the tax on 60 sacks is 3 × 2 = 6 liras,
instead of the stated 2 sacks plus 6 liras, or (2 × 4) + 6 = 14 liras.
Therefore, the deficit is 14 – 6 = 8 liras.
Second, suppose the value of each sack is 8 liras.
Then the tax on 20 sacks, being 1 sack minus 2 liras, is 8 – 2 = 6 liras.
Thus, the tax on 60 sacks is 3 × 6 = 18 liras,
instead of the stated 2 sacks plus 6 liras, or (2 × 8) + 6 = 22 liras.
Therefore, the deficit is 22 – 18 = 4 liras.
By double false position, the correct value of each sack is therefore \[{\frac{(8\times8\,{\rm deficit})-{(4\times4\,{\rm deficit})}}{8\,{\rm deficit}-4\,{\rm deficit}}}=\frac{48}{4}=12\,\,{liras}.\]
To find the tax rate, recall that the tax on 20 sacks was 1 sack minus 2 liras, or 12 – 2 = 10 liras. Thus, the tax rate was 10 liras ÷ 20 sacks = ½ lira per sack.
Check. The tax on 60 sacks was 2 sacks plus 6 liras = (2 × 12) + 6 = 30 liras, for a rate of 30 liras ÷ 60 sacks = ½ lira per sack.
Solution B: algebraic style, by student Alex Wolstencroft (Schoolcraft College)
We are given:
tax on 20 sacks = 1 sack – 2 liras
tax on 60 sacks = 2 sacks + 6 liras.
Multiplying the first equation by 3, we get
tax on 60 sacks = 3 sacks – 6 liras.
Comparing with the second equation,
2 sacks + 6 liras = 3 sacks – 6 liras
2 sacks = 3 sacks – 12 liras
1 sack = 12 liras.
Putting this in the first equation,
tax on 20 sacks = 12 liras – 2 liras
tax on 20 sacks = 10 liras
tax on 1 sack = 10/20 lira = ½ lira.
Solution C: symbolic algebra
Let x = the value of each sack, in liras, and y = the tax on each sack, in liras.
Then we are given:
20y = x – 2
60y = 2x + 6
Multiplying the first equation by 3, we get
60y = 3x – 6.
Comparing with the second equation,
3x – 6 = 2x + 6
x = 12 liras per sack
y = (x – 2)/20 = 10/20 = ½ lira per sack.
Problem 8. A man entered a fair, and the first day doubled all his money and spent 1 gros; likewise on the second tripled all his money that he had left and spent 2 gros; likewise on the third quadrupled his money that he had left and spent 2 gros, and found that he had nothing but 3 gros. I ask how much money he carried [to the fair].
The author showed a solution similar to A below.
Solution A: double false position
First, suppose he entered with 1 gros.
After Day 1: (2 × 1) – 1 = 1 gros
After Day 2: (3 × 1) – 2 = 1 gros
After Day 3: (4 × 1) – 2 = 2 gros instead of the stated 3 gros (deficit 1).
Second, suppose he entered with 2 gros.
After Day 1: (2 × 2) – 1 = 3 gros
After Day 2: (3 × 3) – 2 = 7 gros
After Day 3: (4 × 7) – 2 = 26 gros instead of the stated 3 gros (excess 23).
Therefore, by double false position, the correct amount with which he entered the fair is\[{\frac{(1\times23\,{\rm excess})+{(2\times1\,{\rm deficit})}}{23\,{\rm excess}+1\,{\rm deficit}}}=\frac{25}{24}=1\frac{1}{24}\,\,{gros}.\]
Check.
After Day 1: (2 × 1 1/24) – 1 = 1 1/12 gros
After Day 2: (3 × 1 1/12) – 2 = 1 1/4 gros
After Day 3: (4 × 1 1/4) – 2 = 3 gros.
Solution B: inversion (“working backward”)
Before Day 3: (3 + 2) ÷ 4 = 5/4 gros
Before Day 2: (5/4 + 2) ÷ 3 = 13/12 gros
Before Day 1: (13/12 + 1) ÷ 2 = 25/24 or 1 1/24 gros.
Solution C: algebra
Let \(x =\) the amount with which he entered the fair, in gros.
Then we are given \(4\left[3\left(2x-1\right)-2\right]-2=3,\)
so \[12(2x-1)-8-2=3\] \[24x-12-8-2=3\] \[24x=25\] \[x=\frac{25}{24}=1\frac{1}{24}\,\,{gros}.\]
Problem 9. A vat [of wine] has three spigots, the first bigger than the others, and in such a manner that with the biggest open, all the wine empties in 3 hours; and with the medium one open, it empties in 4 hours; and with the smallest open, it empties in 6 hours. I ask when all the spigots are open together, in how much time will the wine empty.
The author showed a solution similar to A below.
Solution A: single false position
Suppose the time needed to empty 1 vat is 12 hours (chosen purely for convenience, since 12 is divisible by 3, 4, and 6).
In that time, the three spigots together would drain \[\left({\frac{1\,{\rm vat}}{3\,{\rm hrs}}}\times12\,{\rm hrs}\right)+\left({\frac{1\,{\rm vat}}{4\,{\rm hrs}}}\times12\,{\rm hrs}\right)+\left({\frac{1\,{\rm vat}}{6\,{\rm hrs}}}\times12\,{\rm hrs}\right)=9\,\,{\rm vats},\]
instead of the correct 1 vat. Thus, the supposition was too large by a factor of 9, indicating that the correct answer is 12 ÷ 9 = 1 1/3 hrs, or 80 mins.
Solution B: additive rates
Since the rates (vats/hour) are additive, the net rate of drainage is \[\frac{1}{3}+\frac{1}{4}+\frac{1}{6}=\frac{9}{12}=\frac{3}{4}\frac{\rm vats}{\rm hour}.\]
Thus, the net time is \(\frac{4}{3}\frac{\rm hours}{\rm vat}\) or \(1\frac{1}{3}\frac{\rm hours}{\rm vat}.\)
Problem 10. Two men leave on the same day and the same hour from two cities, say for example the first leaves Béziers for Barcelona and the other goes from Barcelona to Béziers. And the one that leaves Béziers does the route in 7 days, and the other takes 9 days. I ask how much time is required before they see each other, and [if the cities are separated by 63 leagues] how far each has traveled.
The author showed a solution similar to A below.
Solution A: single false position
Suppose 4 days are required before the men see each other (chosen for convenience, since 4 is half of the 8-day average of the 7 and 9 days required by each man, respectively, to traverse the entire route alone).
In that time, the two men together would cover \[\left({\frac{1\,{\rm route}}{7\,{\rm days}}}\times4\,{\rm days}\right)+\left({\frac{1\,{\rm route}}{9\,{\rm days}}}\times4\,{\rm days}\right)=\frac{4}{7}+\frac{4}{9}=\frac{64}{63}\,\, {\rm route},\]
instead of the correct 1 route. Thus, the supposition was too large by a factor of 64/63, indicating that the correct answer is 4 days ÷ (64/63) = 63/16 or 3 15/16 days.
The distance covered by each man can then be found by multiplying rate by time:
The first man covers \[{\frac{1\,{\rm route}}{7\,{\rm days}}}\times{{\frac{63}{16}}\,{\rm days}}={\frac{9}{16}\,{\rm route}}={{\frac{9}{16}}\left(63\,{\rm leagues}\right)}={35\frac{7}{16}\,{\rm leagues}}.\]
The second man covers \[{\frac{1\,{\rm route}}{9\,{\rm days}}}\times{{\frac{63}{16}}\,{\rm days}}={\frac{7}{16}\,{\rm route}}={{\frac{7}{16}}\left(63\,{\rm leagues}\right)}={27\frac{9}{16}\,{\rm leagues}}.\]
Check. The total distance covered by the two men is thus 35 7/16 + 27 9/16 = 63 leagues.
Solution B: additive rates
Since the rates (routes/day) are additive, the net rate of speed is \[\frac{1}{7}+\frac{1}{9}=\frac{16}{63}\frac{\rm routes}{\rm day}.\]
Thus, the net time is 63/16 or 3 15/16 days/route. The distance covered by each man can then be found by multiplying rate by time, as in Solution A above.
Solution C: algebra
Using subscripts \(1\) and \(2,\) respectively, to distinguish quantities for the two men, their speeds (rates) are:
\[r_1 =\frac{1\,\rm route}{7\,\rm days}=\frac{63\,\rm leagues}{7\,\rm days}=9\frac{\rm leagues}{\rm day}\]
\[r_2 =\frac{1\,\rm route}{9\,\rm days}=\frac{63\,\rm leagues}{9\,\rm days}=7\frac{\rm leagues}{\rm day}.\]
Since the distances covered by the two men must total 63 leagues, we have \(d_1+d_2=63\) leagues, and so the time \(t,\) in days, required before the men see each other satisfies: \[r_1t+r_2t=63\,\,{\rm leagues}\] \[9t+7t=63\] \[16t=63,\] so that \(t=\frac{63}{16}\) or \(3\frac{15}{16}\) days. The distance covered by each man can then be found by multiplying rate by time, as in Solution A above.
Problem 11. There are 5 men who [each] want to purchase a piece of cloth in such manner [i.e., at such a cost] that the first asks of all the others 1/2 of all the gold and silver they carry, the second asks 1/3, the third asks 1/4, the fourth [asks] 1/5 and the fifth asks 1/6. I ask what the piece cost and what each of them carried.
All solutions differ from one another by an arbitrary multiplicative constant (scaling factor). The author showed, without justification, a rote solution similar to A below. I follow that with my own justification of the rote procedure, and then a solution using matrix algebra.
Solution A: rote procedure
Start with the multiplier 60 (chosen purely for convenience, since 60 is divisible by 2, 3, 4, and 5).
Divide this multiplier by the complements of the stated fractions 1/2, 1/3, …, 1/6:
60 ÷ (1 – 1/2) = 120
60 ÷ (1 – 1/3) = 90
60 ÷ (1 – 1/4) = 80
60 ÷ (1 – 1/5) = 75
60 ÷ (1 – 1/6) = 72.
Add these quotients and divide by one less than the number of men involved:
(120 + 90 + 80 + 75 + 72) ÷ (5 – 1) = 437 ÷ 4 = 109¼,
which gives the total sum carried by the men. The money that each man carried individually is found by subtracting each of the above quotients from this number, one by one:
109¼ – 120 = -10¾
109¼ – 90 = 19¼
109¼ – 80 = 29¼
109¼ – 75 = 34¼
109¼ – 72 = 37¼.
The price of the piece of cloth can be found by subtracting the chosen multiplier from this same number:
109¼ – 60 = 49¼.
Check. We check that each man can meet the price according to his claim:
-10¾ + 1/2(120) = 49¼
19¼ + 1/3(90) = 49¼
29¼ + 1/4(80) = 49¼
34¼ + 1/5(75) = 49¼
37¼ + 1/6(72) = 49¼.
Justification for the rote procedure:
Let \(x_i =\) the money that man \(i\) carries
\({\overline{x_i}}=\) the money that the other 4 men carry
\(T=x_i +{\overline{x_i}}=\) the total money carried
\(c=\) the cost of the piece of cloth
\(x = T – c =\) the excess money.
Taking man 5 as an example, we start with the given condition: \[x_5 +\frac{1}{6}{\overline{x_5}}=c\] \[x_5 +{\overline{x_5}}=c+\frac{5}{6}{\overline{x_5}}\] \[T=c+\frac{5}{6}{\overline{x_5}}\] \[x=\frac{5}{6}{\overline{x_5}}\] \[{\frac{x}{\frac{5}{6}}}={\overline{x_5}}.\]
Similarly, \[{\frac{x}{\frac{4}{5}}}={\overline{x_4}},\,\,{\rm etc.}\] Summing all 5 such equations, we get \[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}={\overline{x_1}}+\cdots+{\overline{x_5}}.\]
Since the money that any one man carries is included in 4 of the 5 terms on the right-hand side, the total on the right is \(4T:\) \[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}=4T\] \[\frac{1}{4}\left[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}\right]=T\]
The parameter \(x\) is an arbitrary multiplicative constant, whose choice determines each \(x_i\) and thus their total, \(T.\) To determine the money that any man carries, say man 5, \[x_5=T-{\overline{x_5}}\] \[x_5={\frac{1}{4}}{\left[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}\right]}-{\frac{x}{\frac{5}{6}}},\]
and to determine the cost, \[c=T-x\] \[c=\frac{1}{4}\left[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}\right]-x.\]
Solution B: matrix algebra
Let \(x_i=\) the money that man \(i\) carries and \(c =\) the cost of the piece of cloth.
The given conditions can be thought of as a system of 5 linear equations and 5 unknowns, with a common parameter on the right-hand side: \[ {\begin{array}{r} x_1+\frac{1}{2}\left(x_2+x_3+x_4+x_5\right)=c\\ x_2+\frac{1}{3}\left(x_1+x_3+x_4+x_5\right)=c\\ x_3+\frac{1}{4}\left(x_1+x_2+x_4+x_5\right)=c\\ x_4+\frac{1}{5}\left(x_1+x_2+x_3+x_5\right)=c\\ x_5+\frac{1}{6}\left(x_1+x_2+x_3+x_4\right)=c\\ \end{array}}\]
In matrix form, this becomes: \[\left[ {\begin{array}{ccccc} 1&{\frac{1}{2}}&{\frac{1}{2}}&{\frac{1}{2}}&{\frac{1}{2}} \\{\frac{1}{3}}&1&{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}} \\{\frac{1}{4}}&{\frac{1}{4}}&1&{\frac{1}{4}}&{\frac{1}{4}} \\{\frac{1}{5}}&{\frac{1}{5}}&{\frac{1}{5}}&1&{\frac{1}{5}} \\{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&1 \\ \end{array}}\right] \left[ {\begin{array}{l} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ \end{array}}\right] =c \left[ {\begin{array}{c} 1\\ 1\\ 1\\ 1\\ 1\\ \end{array}}\right]\]
\[\left[ {\begin{array}{l} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ \end{array}}\right] = c{{\left[ {\begin{array}{ccccc} 1&1/2&1/2&1/2&1/2 \\ 1/3&1&1/3&1/3&1/3 \\ 1/4&1/4&1&1/4&1/4 \\ 1/5&1/5&1/5&1&1/5 \\ 1/6&1/6&1/6&1/6&1 \\ \end{array}}\right]}^{-1}}\left[ {\begin{array}{c} 1\\ 1\\ 1\\ 1\\ 1\\ \end{array}}\right]\]
\[\left[ {\begin{array}{l} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ \end{array}}\right]={\frac{c}{394}}\left[ {\begin{array}{rrrrr} 548&-180&-160&-150&-144 \\ -120&501&-80&-75&-72 \\ -80&-60&472&-50&-48 \\ -60&-45&-40&455&-36 \\ -48&-36&-32&-30&444 \\\end{array}}\right]\left[ {\begin{array}{c} 1\\ 1\\ 1\\ 1\\ 1\\ \end{array}}\right]\] \[\left[{\begin{array}{l} {x_1} \\ {x_2} \\ {x_3} \\ {x_4} \\ {x_5} \\ \end{array}}\right]={\frac{c}{197}}\left[ {\begin{array}{r} -43 \\ 77 \\ 117 \\ 137 \\ 149 \\ \end{array}}\right].\]
If the cost \(c\) is chosen to be \(\frac{197}{4} = 49\frac{1}{4}\), this yields the sample solution found by rote in the Pamiers manuscript, as summarized above.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - About the Author / Acknowledgments
About the Author
Randy K. Schwartz holds degrees in mathematics from Dartmouth College and the University of Michigan. He is a Professor of Mathematics at Schoolcraft College, a community college in Livonia, Michigan, where he has taught since 1984. At Schoolcraft, his teaching focuses on preparing students for careers in engineering, science, health care, and business. Prof. Schwartz is a member of the Commission on the History of Science and Technology in Islamic Societies (CHSTIS), and has participated in several international conferences on the history of Arab mathematics. In 2000, he was awarded the Democracy in Higher Education Prize (National Education Association) for his essay, “Unity in Multiplicity: Lessons from the Alhambra,” an argument for a multicultural approach in mathematics education.
Acknowledgments
The author wishes to thank the editors and two anonymous reviewers for their many helpful suggestions.
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Bibliography
Biggs, Norman, “Mathematics of Currency and Exchange: Arithmetic at the End of the Thirteenth Century,” BSHM Bulletin: Journal of the British Society for the History of Mathematics 24:2 (Jul. 2009), pp. 67-77.
Boag, Elizabeth, “Lattice Multiplication,” BSHM Bulletin: Journal of the British Society for the History of Mathematics 22:3 (Nov. 2007), p. 182.
Davis, Natalie Zemon, “Sixteenth-Century Arithmetics on the Business Life,” Journal of the History of Ideas 21:1 (Jan.-Mar. 1960), pp. 18-48.
Dibner Institute for the History of Science and Technology and WGBH Interactive, “Michael of Rhodes: A Medieval Mariner and His Manuscript” (2005)
http://brunelleschi.imss.fi.it/michaelofrhodes
Goetzmann, William N., “Fibonacci and the Financial Revolution,” pp. 123-143 in William N. Goetzmann and K. Geert Rouwenhorst, eds., The Origins of Value: The Financial Innovations that Created Modern Capital Markets (New York: Oxford Univ. Press, 2005).
Høyrup, Jens, “Questions to the Historiography of Arabic Mathematics Derived from Abbaco Mathematics,” pp. 217-232 in Actes du Huitième Colloque Maghrébin sur l’Histoire des Mathématiques Arabes, Tunis, les 18-19-20 Décembre 2004 (Tunis, Tunisia: Tunisian Association of Mathematical Sciences, 2006).
Hughes, Barnabas, Fibonacci’s De Practica Geometrie (New York: Springer Verlag, 2008).
Labarthe, Marie-Hélène, “Les Règles de Compagnie, dans les Premières Arithmétiques Imprimées des Espagnes: De la Règle Marchande à l’Outil Mathématique,” Revue d’Histoire des Mathématiques 11 (2005), pp. 257–313.
Math Forum, “Lattice Multiplication,” 1996
http://mathforum.org/library/drmath/view/52468.html
Nugent, Patricia M., “Lattice Multiplication in a Preservice Classroom”, Mathematics Teaching in the Middle School 13:2 (Sept. 2007), pp. 110-113.
PedagoNet, “Lattice Multiplication,” uploaded on November 18, 2006
http://www.youtube.com/watch?v=R6uiz8YdA7w
Sanford, Vera, The History and Significance of Certain Standard Problems in Algebra (New York: AMS Press, 1972; originally published 1927).
Schwartz, Randy K., “Combining Strands of Many Colors: Episodes from Medieval Islam for the Mathematics Classroom,” Loci: Convergence, Vol. 7 (August 2010), DOI: 10.4169/loci003546,
http://mathdl.maa.org/mathDL/46/?pa=content&sa=viewDocument&nodeId=3546
Schwartz, Randy K., “Adapting the Medieval ‘Rule of Double False Position’ to the Modern Classroom,” Chapter 5 (pp. 29-38) in Dick Jardine and Amy Shell-Gellasch (eds.), Mathematical Time Capsules: Historical Modules for the Mathematics Classroom (Washington, DC: Mathematical Association of America, 2011).
Sesiano, Jacques, “Une Arithmétique Médiévale en Langue Provençale,” Centaurus 27:1 (1984), pp. 26-75. DOI: 10.1111/j.1600-0498.1984.tb00753.x
Sesiano, Jacques, “The Appearance of Negative Solutions in Mediaeval Mathematics,” Archive for History of Exact Sciences 32:2 (1985), pp. 105-150.
Sigler, Laurence E., Fibonacci’s Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation (New York: Springer Verlag, 2002).
Smith, David Eugene, History of Mathematics, Vol. 2, “Special Topics of Elementary Mathematics” (New York: Dover, 1968).
Spiesser, Maryvonne, “Nombre et Pratiques Calculatoires dans la Tradition Commerciale du XVe Siecle: L’Exemple des ‘Arithmetiques’ du Sud de la France,” in Actes du Colloque “La Pensée Numérique” (Peyrasq, France, 2002). Available from
http://www.peiresc.org/New%20site/Actes.Dhombres/Spiesser.pdf
Spiesser, Maryvonne, “Les Manuels d’Arithmétique pour les Marchands dans la France du XVe Siècle,” Bulletin de l’APMEP [Association des Professeurs de Mathématiques de l' Enseignement Public] 444 (2003), pp. 32-50. Available from
http://www.math.ens.fr/culturemath/histoire%20des%20maths/pdf/Spiesser-marchands_APM-bull.pdf
Spiesser, Maryvonne, Une Arithmétique Commerciale du XVe Siècle: Le Compendy de la Praticque des Nombres de Barthélemy de Romans (Turnhout, Belgium: Brepols, 2004).
Swetz, Frank J., Capitalism and Arithmetic: The New Math of the 15th Century, Including the Full Text of the Treviso Arithmetic of 1478, Translated by David Eugene Smith (La Salle, IL: Open Court, 1987)
Verlinden, O., “Markets and Fairs,” Chapter III (pp. 119-153) in Michael Moïssey Postan, Edwin Ernest Rich, and Edward Miller, eds., The Cambridge Economic History of Europe, Second edition (Cambridge, UK: Cambridge Univ. Press, 1963), vol. 3 (Economic Organization and Policies in the Middle Ages).
Weber, Eugen, “Who Sang the Marseillaise?,” pp. 92-102 in My France: Politics, Culture, Myth (Cambridge, MA: Harvard University Press, 1991).