- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Projective Geometry (The Fano Plane)
April 2008
"I'm thinking of two different simple geometric shapes, one inside the other," you say to a volunteer from the audience. "I want you do to the same thing. Have you thought of something? Please sketch what you imagined, I won't look yet. Earlier, I made a sketch of my own thoughts, I'll show it to you in a moment." Pause.
"Are you finished? I really did want you to do the same thing as me: I tried to project my geometric image to you. We call this projective geometry. Let's see if it worked."
Before the volunteer reveals his sketch, ask other audience members what shapes they had imagined. Several will say a circle inside a triangle, which is what you hope the volunteer has sketched. With surprisingly high probability the volunteer will indeed have opted for that combination; this curious fact is fairly well-known, e.g., see Banachek's Psychological Subtleties (Magic Inspirations, 1998). If this is the combination drawn, turn over a piece of paper on which you've also sketched such an image, to the amazement of all.
Should the volunteer name a triangle inside a circle instead, you can still claim victory. Say, "It's fascinating, you and I thought of the same shapes, but with their roles reversed. I think we have complementary personalities. Such duality is very common in projective geometry." If your luck is out, and the volunteer has the bad taste to mention a square or something equally vulgar, you can always say, "It seems that I was projecting in the wrong direction," indicating somebody who had earlier named the desired circle inside a triangle.
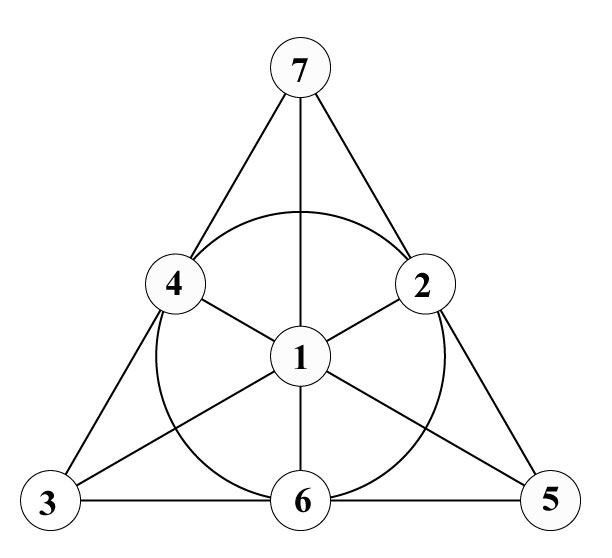
In any case, draw attention to your picture, and continue, "This shape plays an interesting role in a randomization procedure I'd like you to try with me." Re-draw the image on a larger piece of paper or cardboard. This time, inscribe the circle in an equilateral triangle, with seven points and lines marked as shown below.
The image needs to be large enough to accommodate the placement of a card at each relevant intersection point. (Below, these points are marked with empty circles to help the reader to imagine the possibilities in what comes later.)

Fan Actions
Remark that the image depicts the Fano Plane, a delightful mathematical entity representing the smallest finite geometry, of which you are a big fan.
Produce two decks of cards, one blue-backed, one red-backed, and explain that the volunteer is going to determine some random placement of blue-backed cards at the points of the figure, which will in turn determine a particular card from the red-backed deck.
The blue-backed deck is shuffled, and eight cards from it are dealt out into a face-down pile. The volunteer is asked to make choices to determine which four cards he gets, and which four you get. Each of you pickk up and looks at your cards, and arranges them in order (by value) in a fan. Whichever of you has the highest value card sets that aside face-down. This requires comparing high values; one way to pull this off without revealing much is for each of you to hold up your highest card, while turning away, and have the audience indicate which of you has the higher one. You can joke that this card represents the "point at infinity" to a geometer.
The person with the second highest card sets it face-down at the apex of the bounding triangle in the Fano plane. The other person then places any one of the remaining cards in hand at the vertex in the centre of the diagram. This card is also face-down, like all subsequent placements. You each take turns placing cards at the other five points in the figure, until all eight cards have been used up.
Next, the volunteer is asked to push to one side the three cards forming any side of the triangle, after which you push together the remaining four cards. Say, "Which would you like, the three you have indicated, or the four I have here? It's your choice."
No matter which groups of cards is selected, gather up the remaining cards and shuffle them back into the blue-backed deck, which is now removed from the scene to avoid the possibility of confusion later.
Pick up the red-backed deck for the first time, shuffling it openly, and have the volunteer sum the values of the three or four selected blue-backed cards along with that of the ``point at infinity'' card which was set aside earlier.
Turn away and ask that the volunteer look at and remember the red-backed card in the position corresponding to the total just calculated. For instance, you can explain, if he got a total of fifteen, he would look at the fifteenth red-backed card. Have the deck squared up again and turn back.
Do an elimination deal until just one card remains. Stress that it would be a real miracle if the one card left after elimination from a shuffled deck would be the same card the volunteer had looked at earlier. Ask what red-backed card was noted, and have the "last card standing" turned over. They match.
You can now turn over the piece of paper or cardboard to reveal on the other side a written prediction to the same effect.
"Just as projected," you can add in closing. "When one uses the Fano Plane, everything aligns perfectly."
Explain a Ton
Here is a breakdown of the above effect, performance-wise, along with an explanation of why it works.
-
At the outset, the top eight cards of the blue-backed deck are a 3, 5, 6 and 7, followed by an Ace, 2, 4 and 8. The suits are irrelevant, but it's a good idea if they appear random. This stock of cards can be maintained at the top of the deck throughout some convincing looking shuffling. When eight cards are dealt out, this puts the Ace, 2, 4 and 8 on top of the resulting pile.
-
The choices given to the volunteer in selecting his four cards utilize the Bill Simon Sixty-Four Principle, as considered in the April 2006 Card Colm, and recently reviewed in the December 2007 Card Colm. Surprisingly, but crucially, the volunteer ends up with the power of two valued cards: Ace, 2, 4 and 8 (in some order).
-
Alternatively, if the power of two values originally alternate with the other ones at the top of the deck, then the principle explained in "Martin Gardner's Coins to Cards Effect" in the June 2006 Card Colm can be used to ensure that the volunteer gets the desired cards.
-
Announce that each of you must now arrange you cards in order in a fan, keeping the faces close to your respective chests. There is a subtlety here: it's not so important that your cards are in order—although it's a good idea to put the 7 on one end so that you appear above board a little later—but you want to know which card is which in the volunteer's hand. Since you don't officially have any idea what cards he has, this ordering should not raise any suspicions.
-
Each of you now picks out your highest valued card—this is where you need to watch to see which end the volunteer picks his card from—and shows them to an audience member who indicates which is the higher. That card, the 8, the volunteer sets aside face-down. You, having the 7, place it face-down at the apex of the bounding triangle.
-
Next, the volunteer places any of his cards in the centre of the figure. You need to know which card that is, which is easy if his cards are indeed in order in his fan and you saw which end he plucked the 8 from. Place a card below his choice so that yours and his total 7, e.g., if he places the 4, you place the 3.
-
Invite him to fill in the middle of either the left or right side of the bounding triangle, by placing a card there. Again, "match" his choice by secretly using the complement in 7 principle. The other side of the triangle is completed in the same way. Note that the volunteer has filled in the middle "V row" of the figure, and you have filled in the bottom side accordingly.
-
Amazingly, no matter which side of the triangle the volunteer now selects, the three values in question sum to 14, as do the four cards left behind. In fact, up to left-right reflection, one of the following cases must arise.


As a result, adding that total to the value of the card set aside earlier (the 8) leads without fail to 22. The red-backed deck can be shuffled casually if only the top third and bottom half are moved around, without jeapordizing the outcome. Having the volunteer count down to and note the card corresponding to the total arrived at ensures that the original 22nd card is the one remembered, and this is the one whose name you have written in advance as a prediction.
-
The elimination deal with the red-backed deck works like this:
Have the volunteer deal the cards into two piles, A to your left, B to your right,
starting with pile A. Have pile B picked up, and again dealt into two piles, by
first adding to the existing pile A, while creating a new pile B beside it. Have
this repeated, always dealing to pile A first, until just one card remains.
As Stewart Judah published in 1936 (see the December 2004 Card Colm for more information on this deal), that final card is always the one which started in position 22.
-
If you wish, you can ask the volunteer which card was his highest valued one, and when he indicates an 8, you can turn one sideways and say, "I guess I was correct when I said it represented the point at infinity."
The possible arrangements of 1, 2, 3, 4, 5, 6, 7 above correspond to the three essentially different ways that ants in these quantities can be distributed in the seven spaces in the figure below, to that the total number of ants on either side of any of the three lines shown is the same.

Indeed, this month's column was inspired by a puzzle which asked for such arrangements ("Ant-ics" in Ivan Moscovich's wonderful Leonardo's Mirror & Other Puzzles, Sterling, 2004).
While the projective geometry tie-in claimed in the suggested presentation is a bit of a stretch, there is a duality between that last figure above and the original Fano plane. The seven regions inside the above circle correspond to the seven points in the first figure considered, and two of those regions are adjacent iff the corresponding points in the first figure are connected by a line.
Furthermore, if the volunteer names a triangle inside a circle as his thought-of combination, you could produce the last figure--saying "in mine I continued the triangle sides till they met the circle"--and adapt the patter (and mathematics) accordingly.
It goes without saying that an actual performance of every step as outlined above is not for the faint of heart. Many shortcuts are possible, from streamlining the "free choice of four card from eight" part to the total elimination of the elimination deal (and the second deck). The latter option suggests turning the trick into a book force: you can predict ahead of time the first word on page 22 of a book of your choice.
Many thanks to Scott Hudson (of Direct Data Communication) for providing all of the images used above, and to magician Joe M. Turner for the Banachek reference.
"Fan actions" is one of several interesting anagrams of "Fano antics."




