- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Three Piles (This Isn't That Trick)
November 2010
Hand out a deck of cards for thorough shuffling. Take it back and fan it face-up, commenting on how randomly mixed it now is. Casually drop several clumps of cards on the table, and set the rest of the deck to one side. Straighten up the clumps of cards into three stacks of five cards, which will look something like this:

Address one of your audience. "When I turn away in a moment, I want you to remove any one of the cards in these three piles, noting its position carefully, and replace it with a card of your choice from the remainder of the deck, switching red for black or vice versa. Make sure you remember the new card, and insert it in the same position as the removed card in one of these piles. Finally, hide the jettisoned card in the rest of the deck, and set it aside."
Once you are convinced that these instructions have been understood, turn away, and have the switch done. Turn back, gather up and combine the three stacks in any order, and turn the resulting packet of fifteen cards face down. Deal face up from left to right into three overlapping columns or piles. For instance, in the gathering and combining stage, if the pile above with the 6♣ is placed on top of the pile with the 8♤, and these are placed on top of the pile with the Q♥, the result of the dealing would be three columns or piles like this:

Say, "You may be familiar with a trick in which the magician deals three piles of cards like this, and then asks you to mentally pick one card, but not reveal which one it is. This isn't that trick."
Let that sink in, then continue, "Of course, you've already got a special card in mind, please note its position here, but don't tell me anything."
Point at the three piles and say, "It's customary now for the magician to ask you to indicate which pile your card is in, and then gather the piles so that the one you indicate is in the middle." Pause, and then say, "This isn't that trick. You may think about which pile your card is in, but don't point or say a word. If you like, try to communicate the information to me with brainwaves."
Gather the three piles, face up, from right to left. In the situation above, the pile with the 6♣ on top goes on top of the pile with the J♦, on top, and the pile with the 9♦ on top goes underneath those. Turn this packet face down, then deal the cards face up into three new piles from left to right. For the piles above, the second display looks like this:
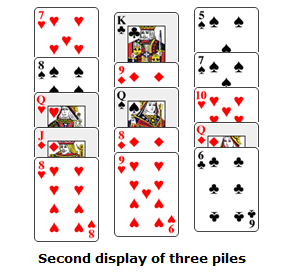
Say, "At this point it's not unusual for the magician to ask you a second time to indicate which pile your card is in, and then gather the piles once more so that that pile is in the middle." Pause again, and say, "This isn't that trick. Again, feel free to note to yourself which pile your card is in, but this time don't try any of that brainwaves stuff. I must remain completely in the dark."
Gather up the three piles a second time, face up, from right to left. Turn this packet of fifteen cards face down, then deal the cards one more time, face up, into three new piles from left to right. For the last piles shown above, this third display will look like this:
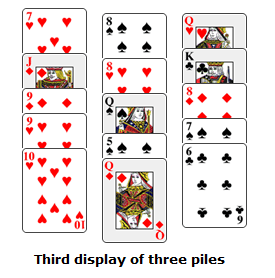
"Would you be impressed if I could now identify your card?" you ask nonchalantly. Regardless of the answer—and brushing aside as necessary any suggestions that you might have a photographic memory, and can actually recall all of the original fifteen cards used—continue. "Alas, I can't do that. Remember, this isn't that trick." Act as if the trick is over, picking up and pocketing the set-aside deck.
Theatrical Sweep
Suddenly, say dramatically, "Wouldn't it be a lot more impressive if somebody who has seen none of what has just happened could identify your card?"
With further ado, have your mathemagical accomplice Jeff—whose very existence was perhaps previously unknown to all assembled—summoned from a nearby room. Ask that the identity of the special card be communicated to him telepathically. Say, "I've done most of the work so far, now it's time for you to do your bit. Jeff here will apply his telepathic wares; let's see how he fares."
Watch jaws drop all around, as Jeff absorbs the projected brainwaves, and soon points to one specific card, which is promptly confirmed to be the chosen one.
Needless to say, the communication is entirely mathematical—Jeff simply studies the display of cards—and has nothing to do with any spoken or physical cues.
Await (Secret) Help
When you first get back the shuffled deck, and scan the card faces, you must look for three (not necessarily different) runs of any of the following four types:
-
Black, Black, Black, Black, Black
-
Black, Red, Black, Red, Red
-
Red, Black, Red, Black, Red
- Red, Red, Red, Red, Black
(Avoid the all black one if you fear it's "too obvious.") It's quite likely that you will indeed locate three such runs, in which case casually drop these as clumps on the table. In the unlucky event that some of the desired runs prove to be elusive, simply drop smaller clumps on the table in such a way that the assembled stacks form the desired runs.
With the convention that 0 = Black and 1 = Red, the card runs above correspond to a (very small, and not very efficient) error-correcting binary code, in which (a, b, a, b, a + b) encodes (a, b). The "additional" (a, b, a + b) are known as parity check digits (or bits).
| Message | Check digits |
| 00 | 000 |
| 01 | 011 |
| 10 | 101 |
| 11 | 110 |
A single switch (of 0 for 1 or vice versa) in such a run of five bits is easy to detect and not hard to correct. Figuring out exactly how to do this is a good exercise, and the details can be gleaned from the October 2009 Card Colm, which was based on "Horses In the Stream and Other Short Stories" from the book Homage to a Pied Puzzler (A.K. Peters, 2009), Once again, we are indebted to the author of that piece, Earnest Hammingway, for allowing us to use some of his ideas here. Note that the decoding here is a lot easier than it was there, as it's entirely binary; the actual card values play no role. Alternatively, this month's Card Colm could be implemented based on parity instead of red/black considerations, though this makes the requested switch a little trickier to direct.
Telepathic Wares
Given that the three pre-switch stacks of cards are correctly coded, it's not difficult for Jeff to quickly check the final display, and figure out which card is decidedly "off-colour".
To see why, one must understand the relationship between (1) The arrangement of the cards in the three initial stacks (before or after one switch), and (2) The resulting display after all of the pickups and dealing.
We purposely hid most of the cards in the initial stacks earlier to obscure this connection. It's time to put all of our cards on the table. This is what the original three stacks at the very start above would have looked like, after the card switch, and before any gathering and dealing, had they been spread out for all to see:

Can you now guess what Jeff looks for when he sees the third and final display? It would be more fair to ask this question after showing the following display, in view of the order in which we earlier suggested picking them up.

(Such a display would be picked up in the oft-suggested "right, center, left order" so as to lead to the first display of three piles above after one round of dealing.) Compare that with the third display of three piles above and you should notice something significant! Jeff can now locate the three runs, and check each one as to whether it's correctly coded, knowing full well that exactly one of the three will fail. He then figures out how to correct that run, hence honing in on the switched card.
To make the before/after display relationship easier to follow, forget all about coding, and simply focus on the obvious patterns in these (error-free) piles:

These represent the original three stacks, regardless of card switching, displayed as columns. It doesn't matter in which order the piles are picked up the first time; just to keep it simple assume that it's right, center and left as in all of the subsequent pick-ups. After this first pick-up and new deal we have:
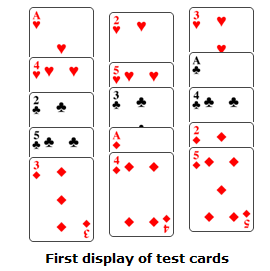
After the second pick-up and new deal we have:

After the third pick-up and new deal we have:

While this isn't perfect—the original three piles are only half way to being reconstructed—upon reflection, or more correctly upon rotation, the starting piles can be read off from here. The middle one is intact, but reversed, and the other two are close to being intact (and also reversed). Curiously, we seem to have a rotation with three fixed points!
Jeff first scans the middle pile bottom to top seeing if it's correctly coded (in which case the switched card is not there), or not (in which case he can tell which of these is the switched card). If this middle pile is okay, he moves on to consider the bottom four cards in the first pile together with the first card in the last pile. If those are okay—in the sense that there's no error detected—he looks at the top left card followed by (in reverse order) the top four cards of the last pile. In all cases he will be able to identify the one card that is out of place.
For the cards shown earlier on, in the third display of three piles, he'd find that the 5♤ is the odd man out: indeed looking at the zeroth display of three piles above, we can see that the first column (read from top to bottom) is not consistent (i.e., correctly coded) because of the black card in the second position.
Hamming It Up
The famous (though admittedly tedious) trick which we've modelled the above presentation on is generally done with three piles of seven (or nine) cards. We opted for five cards in each pile as the dealing is quicker, and it ties in with the "baby" linear binary code used, whose associated mental gymnastics can—with practice—can be done speedily. It turns out that such five by three arrays cycle back to their original configurations after six rounds of picking up and dealing, and even better, their initial arrangements can be deduced half way through this process, i.e., after only three rounds of picking up and dealing.
More ambitious readers may wish to try the effect using three piles of seven cards, together with the standard entry-level Hamming binary code which encodes four bits with three check bits. It's more work to find three appropriate runs of seven cards in a shuffled deck, however many more types are now available. It's also more work for an accomplice to decode and stop the one error known to be there after a single red/black (or parity) switch.
The good news is that such seven by three arrays cycle back to their original configurations after just four rounds of picking up and dealing, and even better, their initial arrangements can also be deduced half way through this process, i.e., after only two rounds of picking up and dealing.
Oddly enough, the situation for six by three arrays is not nearly as nice.




