- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Frank Morgan's Math Chat - Pizza Pie
 |
 |
August 16, 2001
Old Challenge (William K. Scherer). What is the best way to cut a square pizza into three pieces, each with the same amount of pizza and with the same amount of crust?
("I came upon this whilst deciding how to divide the sole remaining Klondike bar in the freezer between myself, my wife, and my 2.5 year old son. (Un)Fortunately, my wife had already eaten the last one, so I never had to solve it! But it intrigued me just the same. I have no solution yet...")
Answer. R. Weirauch and Scherer provide these solutions:
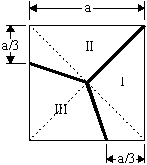
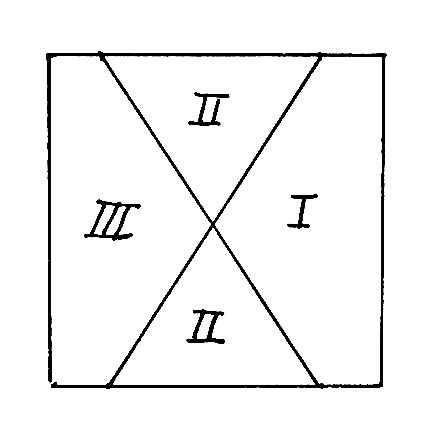
The first uses just three cuts, and one could argue that the second uses just two.
Eric Brahinsky shows that any slices (cut from the center) with equal lengths of crust automatically have equal areas of pizza. Indeed, suppose that the pizza is 2 by 2. Now if, for example, the slice is a single triangle, then its area is
.5 x base x altitude = .5(length of crust)(1) = half the length of its crust .
If a slice includes a corner, it might be two triangles, but its area would still be half the length of its crust. So if the crust is evenly divided, the whole pizza is evenly divided too.
New Challenge (National Public Radio Weekend Edition Puzzle 7/29/01). Complete the following to a magic square, in which each column, each row, and both diagonals sum to 1.
|
A MATHEMATICIAN AT HEAVEN'S GATE drew this response from Mark Thompson: Actually, your "Mathematician in Heaven" reminds me of a little snatch of dialog I composed once about Goldbach and his conjecture than every even natural number is the sum of two prime numbers. I imagined the scene between Goldbach and God, after the former went to his reward:
GOLDBACH: Now that I'm here, at last I can ask you whether my famous Conjecture is really true!
GOD: It is.
GOLDBACH: I knew it! Then, do not keep me in suspense, but tell me the proof -- WHY is every even number the sum of two odd primes?
GOD: No particular reason. Just so happens.
GOLDBACH: What? Why, without a proof, how can one KNOW that this is true? GOD: Well, being infinite, I merely perceive its truth for each of the even numbers, separately and simultaneously. You can't do that, obviously, so you must take My word for it. GOLDBACH: But -- but -- but this is highly unsatisfactory! GOD: You humans have such a problem with being finite -- ever since I first defined you, back in Eden. Adjust!
Copyright 2001, Frank Morgan.
Send answers, comments, and new questions by email to Frank.Morgan@williams.edu, to be eligible for Flatland and other book awards. Winning answers will appear in the next Math Chat. Math Chat appears on the first and third Thursdays of each month. Prof. Morgan's homepage is at www.williams.edu/Mathematics/fmorgan.
THE MATH CHAT BOOK, including a $1000 Math Chat Book QUEST, questions and answers, and a list of past challenge winners, is now available from the MAA (800-331-1622).




