- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Innovative Teaching Exchange: In Search of the Elusive Matrix
by David E. Meel
Bowling Green State University
Imagine a linear algebra class where you have just completed discussing concepts such as null and column spaces, bases, and dimensions. Now picture a stack of journals, many of them revealing students' difficulties with understanding these ideas. There are too many new, related concepts, and at first they're hard to distinguish. I developed a guided exploration which compelled students to work together, to use the concepts' definitions, and to explore the details of these concepts with some guidance.
When designing the activity, I kept in mind that the Linear Algebra Curriculum Study Group mentioned that "... students learn best, as we do, by active involvement - solving problems, making conjectures, and communicating with others" [2]. I decided that the activity had to employ a variety of tasks [3], to probe the connections between symbols, symbolic procedures and problem-solving procedures [3], to be diverse in terms of complexity and dissimilarity from those presented in the learning situation [1], and to cause students to build connections, fold-back, or validate thinking [5]. In particular, the activity was designed to help students coordinate their understandings of dimension, basis, null space, and column space by taking a new perspective different from that presented in David Lay's Linear Algebra and It's Applications text [4], class, or homework.
A Look at the Activity
The exploration began with questions designed to give students a sense of accomplishment and then posed questions constructed to motivate and guide the exploration. In particular, the activity was segmented into a series of three hand-outs with each having its own "milestone". These milestones would be the recognition of integral aspects of the problem situation permitting the students to make the next step in the exploration.
My class of students was divided into working groups (5 or 6 students) and once they were organized, the first hand-out of questions was given to the students. It looked like this:
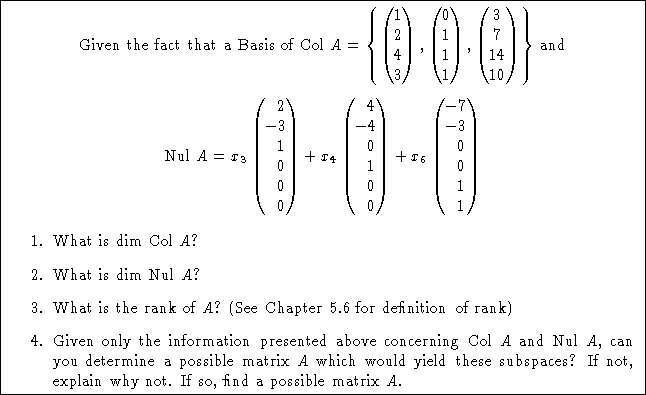
Figure 1: Initial hand-out questions to get the investigation started
The first two questions (a & b) were quite accessible since they had been part of homework problems from previous sections. The third question (c) introduced a new term which had not been mentioned previously in class. Students scrambled to get their books and look up this new term and come to the realization that "Oh, the rank of A is simply equivalent to dim Col A!" The last question (d) was designed to get the students to begin searching for the matrix A. The only clues to the nature of the matrix were the given descriptions of Col A and Nul A. Being accustomed to homework problems asking for Col A and Nul A when given a matrix, students had not considered how these could be used to describe a matrix. As I walked around the classroom, I overheard students questioning each other, explaining ideas, looking at their textbooks, and making conjectures about what they could do to answer this last question. As each group reached the first milestone of a conclusion concerning the possibility of finding the matrix, I walked over to discuss their ideas. I took this opportunity to agree and disagree with statements, answer questions, and interject ideas. Once I was satisfied that students' planned to use the tacit data from the basis for Col A and description of Nul A to reconstruct the matrix A, I gave them the second hand-out of questions to help them in their exploration:

Figure 2: Questions on the second hand-out
Now students had to reexamine the definitions of null and column space and the procedures used to find descriptions of these spaces from a given matrix. It was at this phase that my students struggled the most. They were used to looking at an ![]() matrix and finding out the m and n; however, using the information from Col A and Nul A to obtain the values of m and n was another story. I could hear students asking things like "Is Nul A associated with row or column vectors?" and others responding with "It must be associated with row vectors because what else would Col A be associated with except column vectors!" But even this realization did not lead all students to the size of the matrix since some were confused about whether the number of vectors or the size of the vectors in Col A and Nul A should be used to get this information. It took students a long time to figure out that they could use ideas like dim Col A + dim Nul A = rank A + dim Nul A = n and that the number of rows in the vectors for the Basis of Col A identify the m of a
matrix and finding out the m and n; however, using the information from Col A and Nul A to obtain the values of m and n was another story. I could hear students asking things like "Is Nul A associated with row or column vectors?" and others responding with "It must be associated with row vectors because what else would Col A be associated with except column vectors!" But even this realization did not lead all students to the size of the matrix since some were confused about whether the number of vectors or the size of the vectors in Col A and Nul A should be used to get this information. It took students a long time to figure out that they could use ideas like dim Col A + dim Nul A = rank A + dim Nul A = n and that the number of rows in the vectors for the Basis of Col A identify the m of a ![]() matrix to find the m and n of the
matrix to find the m and n of the ![]() matrix A.
matrix A.
When students came to the question concerning free and determined unknowns, they recognized the terms but were not sure how to use the given information to answer the question. It took a while but finally students started to exclaim "Hey, we can use the description of Nul A to figure this out!" This led students to the next step, to use what they knew about Nul A to reconstruct the row reduced version of matrix A. Students had difficulty coordinating issues such as echelon form, reduced-echelon form, free variables, basic variables, and pivot columns. In particular, one of the major difficulties students faced was formulating the following string of implications:
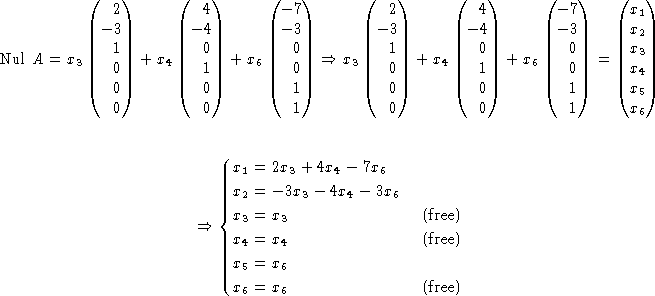
Figure 3: A possible string of thinking to obtain the reduced echelon form of A
Once students were able to accomplish this, there was much discussion as to how to take the information and generate the matrix as well as where the ones and zeros should go. Eventually, students were able to generate a version of the reduced matrix corresponding to A:
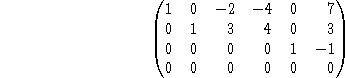
The last question required synthesis of the investigation to construct a general matrix given the information provided. Students struggled with developing a general matrix which included the specific basis elements of Col A due to the interaction of specificity and generality. Students were able to recognize that they needed a general matrix but wanted to somehow incorporate the information from Nul A also. After much conversation within individual groups, students realized that the general matrix would be constructed from the components of the description of Col A but would include some unknowns. The unknowns seemed to really bother the students until they realized that the general matrix would be "row reduced" to obtain the matrix (see figure 5) found from the examination of Nul A. As a result, students were ultimately able to generate the matrix
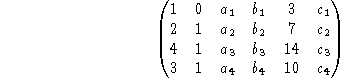
Once students identified the initial state, the final state, and the process to move from the one to the other, I passed out of the next handout (see figure 4) containing the row reduction process.
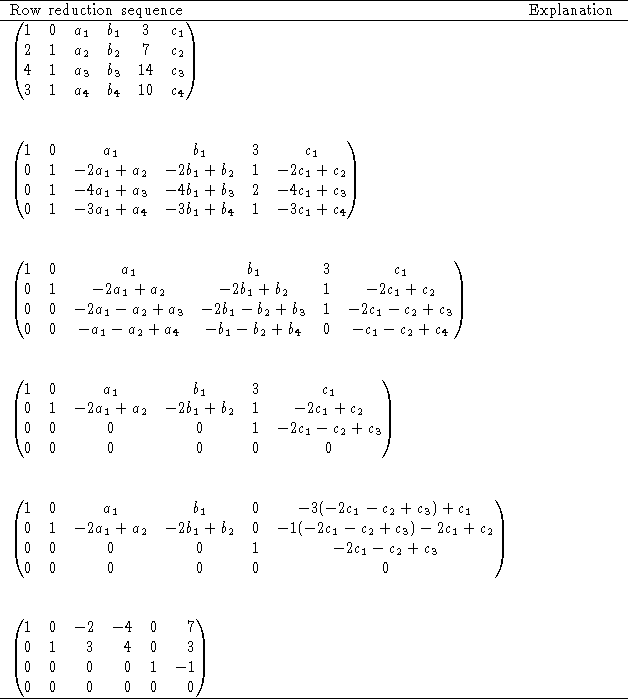
Figure 4: The third hand-out showing the row reduction sequence
Students had to follow and explain the row reduction sequence. The final step of the activity required students to use this information to determine the values for ![]() ,
, ![]() , and
, and ![]() . To accomplish this, students had to solve three systems of equations (see figure 5).
. To accomplish this, students had to solve three systems of equations (see figure 5).
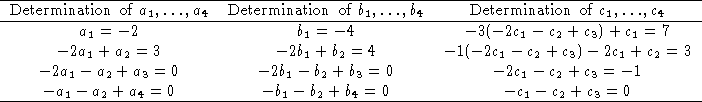
Figure 5: Three systems of equations necessary to determine a reconstruction of matrix A
Students chose substitution and transformation into matrix equations as methods for solving the systems. As a result, the activity came full circle to arrive at the matrix
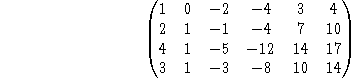
An extension of the activity would be to determine if there are other possible matrices which would provide similar Null and Column spaces.
Implications of the activity
The activity really helped them conceptualize the material better. One student said, in a journal entry, "... It really summed up the previous sections and I now have a clean and concise understanding" which was the goal of designing and implementing the activity in my class. By having students work together, they struggled with the definitions, argued over ideas, and taught each other. The impact of this experience was evident in students' responses to a question on the final exam:
For a given ![]() matrix A, define null space, column space, and row space. In addition, for each of these, describe how the dimension is obtained and where rank A fits in.
matrix A, define null space, column space, and row space. In addition, for each of these, describe how the dimension is obtained and where rank A fits in.
Students were generally able to situate the concepts of null and column spaces, basis, and dimension to provide reasonably coherent discussions of the ideas.
References
- Brownell, W.A. & Sims, V.M. (1946). The nature of understanding. In J.F. Weaver & J. Kilpatrick (Eds.) (1972), The place of meaning in mathematics instruction: Selected theoretical papers of William A. Brownell (Studies in Mathematics, Vol. XXI, pp. 161-179). Stanford University: School Mathematics Study Group. (Originally published in The measurement of understanding, Forty-fifth Yearbook of the National Society for the Study of Education, Part I, 27-43.)
- Carlson, D., Johnson, C.R., Lay, D.C., & Porter, A.D. (1993). The linear algebra curriculum study group recommendations for the first course in linear algebra. College Mathematics Journal, 24(1), 41-46.
- Hiebert, J. & Carpenter, T.P. (1992). Learning and teaching with understanding. In D. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 65-97). New York, NY: Macmillan.
- Lay, D.C. (1996). Linear Algebra and Its Applications. Reading, MA: Addison-Wesley.
- Pirie, S.E.B. & Kieren, T.E. (1991). A dynamic theory of mathematical understanding: Some features and implications. (ERIC Document Reproduction Service No. ED 347 067)
David E. Meel (meel@math.bgsu.edu) is an assistant professor at Bowling Green State University. His research interests include the effects of alternative assessments, the mathematical understandings of prospective teachers, and the teaching and learning of undergraduate mathematics with particular attention to calculus, linear algebra, algebra, and geometry.
The Innovative Teaching Exchange is edited by Bonnie Gold.
|
Go to...
|
Find out...
|




