- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Right Triangles and Elliptic Curves
Given a natural number d, is there a right triangle with rational sides and area d?
 Noted number theorist Karl Rubin of the University of California, Irvine addressed this question in last month's Distinguished Lecture at the MAA's Carriage House Conference Center in Washington, D.C. He showed how studying a seemingly simple query about right triangles gives rise to intriguing puzzles and deep results in number theory, with links to elliptic curves and the famous Birch and Swinnerton-Dyer conjecture.
Noted number theorist Karl Rubin of the University of California, Irvine addressed this question in last month's Distinguished Lecture at the MAA's Carriage House Conference Center in Washington, D.C. He showed how studying a seemingly simple query about right triangles gives rise to intriguing puzzles and deep results in number theory, with links to elliptic curves and the famous Birch and Swinnerton-Dyer conjecture.
The son of mathematician and physicist Robert Rubin and astronomer Vera C. Rubin, Karl Rubin grew up in Washington, D.C. He received his bachelor's in mathematics from Princeton University and his doctorate from Harvard University in 1981. He worked at Princeton, Ohio State University, and Stanford before moving to Irvine. In 1992, he received the prestigious Cole Prize in Number Theory, awarded by the American Mathematical Society.
Rubin is best known for his work in number theory on elliptic curves, certain cubic equations that played a major role in the proof by Andrew Wiles of Fermat's last theorem. Studying elliptic curves can lead to insights into many parts of number theory, including finding rational right triangles with whole-number areas.
Suppose, for example, that the given area is 6. A right triangle with sides 3, 4, and 5 is one example that has the requisite area. For area 5, a right triangle with sides 3/2, 20/3, and 41/6 would work.
The Pythagorean theorem states that a triangle with sides a < b < c is a right triangle if and only if a2 + b2 = c2. This triangle has area d = ab/2. Hence, we can restate the original question in the following form: Are there rational numbers a, b, c > 0 such that a2 + b2 = c2 and ab = 2d? If the answer is "yes", number theorists call d a congruent number (not to be confused with congruence modulo an integer).
So, the original question amounts to a search for what are, in this context, congruent numbers.
Over the years, mathematicians have devised several ways to approach the problem, showing the existence of triangles with rational sides for areas 5, 6, 7, 41, and other values. However, even when we know that a rational right triangle of a certain area should exist, finding it can be difficult. For example, the simplest rational right triangle with area 1063 has shortest side a where the numerator of a has 104 digits and the denominator has 103 digits.
To find and explore such relationships, we can translate the problem of finding rational right triangles with a given area into a question about rational solutions of specific elliptic curves.  Audio
Audio
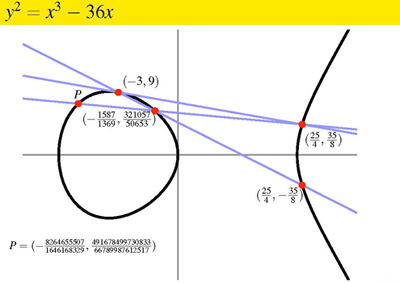
For example, the (3, 4, 5) triangle with area 6 gives the solution (–3, 9) of the elliptic curve y2 = x3 – 36x. Moreover, if an elliptic curve has one rational point, it has infinitely many rational points. So, there are infinitely many rational right triangles with area 6.
Intriguingly, when we list in order the shortest side of rational right triangles with area 6, the table has a distinctly parabolic form.

The shortest side of some right triangles with area 6.
Describing the insights that could be gleaned from an elliptic-curve perspective, Rubin delved into various problems and mysteries involving congruent numbers; for example, finding ways to decide whether a given elliptic curve has infinitely many rational points. His discussion led to the Birch and Swinnerton-Dyer conjecture, which posits that an elliptic curve has infinitely many rational points if a certain function has the value 0. The Clay Mathematics Institute has offered a prize of $1 million for a proof of the conjecture.
Rubin closed by describing some open questions, noting that much remains to be done in the realm of right triangles and elliptic curves.  Audio
Audio
An earlier version of Rubin’s talk on right triangles and elliptic curves can be found in Mathematical Adventures for Students and Amateurs, published by the MAA.
 Listen to Karl Rubin's lecture (mp3)
Listen to Karl Rubin's lecture (mp3)

This MAA Distinguished Lecture was funded by the National Security Agency.




