Virginia State University

Title: A Study of Bernstein Inequality for Self Reciprocal Polynomials of Degree Two and Related Subclasses

Director(s): Dawit Haile

Dates of Program: May 21 - June 30, 2007

Summary: Denote the class of all algebraic polynomials of degree at most n by P_n. It is well known from Bernstein's Theorem that . Equality holds if and only if p(z) = czⁿ, c is a constant.

This inequality has been improved under several kinds of restrictions. Consider a subclass 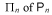consisting of all polynomials 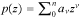which has the property p(z) = zⁿp(1/z). The question is if 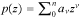, what is the best estimate of in terms of ?

Using basic results from Complex Analysis and knowledge of Trigonometry and Calculus, students will explore the case when n = 3. They will also give an alternative proof for the known case when n = 2.

Student Researchers Supported by MAA: