- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers

Publisher:
Princeton University Press
Publication Date:
2014
Number of Pages:
296
Format:
Hardcover
Price:
27.95
ISBN:
9780691154633
Category:
General
[Reviewed by , on ]
Tushar Das
01/13/2015
The book being reviewed was born in the “contemplative silence” taking place among late-evening conversations between a musicologist, a psychologist and the author, as they “sniffed and sipped expensive Barolo” at a local enoteca on Lake Como. As Mazur recollected in 2012, “My forthcoming book, Enlightening Symbols, is primarily about mathematical symbols, yet its essence is a consequence of recalling innumerable distinct conversations ever since that one night at Cava Turacciolo.” (One may read the entire account at the Guggenheim Foundation website.)
A Barolo-infused atmosphere continues to linger in the personable tone that pervades Mazur’s tour through the historical labyrinths of mathematical notation, both numerical and algebraic. You could almost imagine him sitting across from you, a bottle of thought-provoking wine in between. Before reading my minor criticisms, I strongly recommend Georges Szpiro’s glowing review that is available via Mazur’s website.
Mazur describes his goal at the end of the introduction:
The book traces the origins and evolution of established symbols in mathematics, starting with the counting numbers and ending with the primary operators of modern mathematics. It is chiefly a history of mathematical symbols; however, it is also an exploration of how symbols affect mathematical thought, and of how they invoke a wide range of enduring subconscious inspirations.
The books is split in three parts. The first on numerals takes up about 37% of the book, the second on algebra, 43%. The last part, titled “The Power of Symbols”, is much shorter and somewhat impressionistic. It touches on a myriad metamathematical themes: philosophy, psychology, cognition, etc. For example, it gives a snapshot of the work of the neuroscientist Stanislas Dehaene and his collaborators. I felt that Mazur was at his weakest in these last five chapters, and that the reader may well be unsatisfied with his exploration of “how symbols affect mathematical thought, and of how they invoke a wide range of enduring subconscious inspirations.” However the topics and themes are certainly thought-provoking, Barolo notwithstanding! The book does include a beautiful map/timeline titled The Significant Initiators that I hope Mazur will place on his website for students to peruse and hopefully improve upon, e.g. to produce an enhanced poster-size version!
Though Mazur promises us a history up to the “primary operators of modern mathematics”, he stops somewhere after the primary operator of the differential calculus. For instance, there are no limits, no infinite series (only a single instance of a “\(\Sigma\)” in the penultimate paragraph of the last chapter) and no integral (apart from an incongruous instance hidden in an appendix). Similarly one will not find determinants, absolute values, function notation of one and several variables, logical symbols, vectors, differential operators from vector calculus, tensors, the vast edifice of differential geometric notation and the powerful Einstein summation convention, etc. In Mazur’s defense, his publishers may have warned against throwing in a surfeit of sales-reducing notation. A good source for more information is The Earliest Uses of Mathematical Symbols, a web site maintained by Jeff Miller, which is somewhat easier to navigate than Cajori's famous A History of Mathematical Notations.
Nevertheless, it is a pity that giving some sense of the explosion of modern mathematical symbolism in the 20th century that continues up to this day, some idea of the scope (and downsides?) of our ever-growing forest of symbols, was not to be a part of Mazur’s project. What would his readers have made of diagrams, e.g. homological algebra’s infamous Snake Lemma (cf. Jill Clayburgh in It’s My Turn) or, the Frobenius equation from two-dimensional topological quantum field theory:
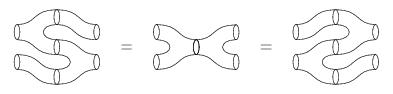
The Frobenius equation
Source: J. Kock’s webpage Remarks on the origin of the Frobenius equation
There is a problem on p.139: “Although Euler was the one who introduced us to the symbol \(i\) for the imaginary number \(\sqrt{-1}\), it didn’t appear again until Gauss used it in 1867.” Of course, Gauss died in 1855. The error is not repeated in the appendix on quarternions on p. 231, which correctly paraphrases Cajori’s A History of Mathematical Notations (cf. p. 128 of the 1993 Dover reprint, with the reviewer’s insertions in bold):
Had Euler not marked \(\sqrt{-1}\) as \(i\) in a memoir presented to the Academy at St. Petersburg in 1777, had \(\sqrt{-1}\) not been published in 1794 after his death [see Figure 2 below], had Gauss not made consistent use of \(i\) after 1801 [in his Disquisitiones Arithmeticae], the quaternions may have not been discovered so soon in the history of the subject to make their vital contributions to mathematical physics.
— which, per se, is an interesting thesis. It would be of interest to know whether Hamilton ever expressed such a debt or acknowledged a source of inspiration. For the reader’s pleasure and as a homage to Euler, I include a snapshot of the text (published 1794) where Euler denotes \(\sqrt{-1}\) by \(i\).

From L. Euler (E671) De formulis differentialibus angularibus maxime irrationalibus, quas tamen per logarithmos et arcus circulares integrare licet, a paper written in 1777 (the year of Gauss’s birth), but published posthumously in Institutiones calculi integralis 4, 1794, pp. 183–194.
Source: Euler Archive.
Finally, I felt that Leibinz’s role was given somewhat short shrift. This in spite of a two-page appendix on his “\( \frac{dy}{dx}\)” notation and a brief (just over three pages) chapter dedicated to him, viz. Chapter 18: The Symbol Master, whose title harks back to Florian Cajori’s “Leibniz, the Master-Builder of Mathematical Notations (Isis, Vol. 7, No. 3 (1925), pp. 412–429). We quote from the Leibniz scholar E. Knobloch’s Leibniz between ars characteristica and ars inveniendi: Unknown news about Cajori’s ‘master-builder’ of mathematical notations, which appeared in Albrecht Heeffer, Maarten van Dyck (eds.), Philosophical Aspects of Symbolic Reasoning in Early Modern Mathematics (London 2010, 289–302):
Leibniz spent his entire life trying to perfect and organize the ars inveniendi [the art of inventing new theorems, new results, new methods], the ars characteristica [the art of inventing suitable characters, signs], and the ars combinatoria [the art of combination]. These three arts were, in his view, inseparably connected. The methodically pursued expansion of knowledge, the ars inveniendi, was decisively based on the suitable choice of characters, of signs, such as those invented by the ars characteristica. Meanwhile, the ars combinatoria provided the rules according to which the characters created were to be manipulated to create new knowledge: in his eyes it was a general science that teaches a merely syntactical manipulation of signs.
Mazur mainly steers clear of the integral and its now ubiquitous notation, which is also due to Leibniz. We quote from Cajori (op. cit. p. 414) for some background on this incongruous affair:
The delay of Leibniz in letting his sign of integration \(\int\) appear in print cost him temporarily the recognition on the Continent of being the first inventor of the integral calculus. Johann Bernoulli had been active in this field and was looked upon as the creator of the integral calculus. At one time Leibniz and Johann Bernoulli discussed in their letters both the name and the principal symbol of the integral calculus. Leibniz favored the name “Calculus summatorius” and the long letter \(\int\) as the symbol. Bernoulli favored name “Calculus integralis” and the capital letter \(I\) as the sign of integration. The word “integral” had been first used Jakob Bernoulli. Leibniz and Johann Bernoulli finally reached a happy compromise, adopting Bernoulli’s name “Integral calculus” and Leibniz’s symbol of integration.
It may be interesting to note that Johann Bernoulli’s notation did resurface in certain modern analysis texts when the integral was interpreted as a functional via the Riesz representation theorem, as in Cohn’s Measure Theory or in Segal and Kunze’s Integrals and Operators (Springer 1978).
As I have mentioned before, my criticisms are very minor. The book is not intended to be a work of historical scholarship, but rather an invitation to look more closely at mysteries right under our noses, and to think about pathways often taken for granted. Mazur does an excellent job of weaving together a wonderful culturally-rich tapestry, within which he threads the evolution of mathematical notation. His theme is a “tough sell” and therefore the Guggenheim Foundation and his publishers at Princeton University Press should be commended for supporting such an endeavor.
Tushar Das is an Assistant Professor of Mathematics at the University of Wisconsin–La Crosse.
Introduction ix
Definitions xxi
Note on the Illustrations xxiii
Part 1 Numerals 1
1. Curious Beginnings 3
2. Certain Ancient Number Systems 10
3. Silk and Royal Roads 26
4. The Indian Gift 35
5. Arrival in Europe 51
6. The Arab Gift 60
7. Liber Abbaci 64
8. Refuting Origins 73
Part 2 Algebra 81
9. Sans Symbols 85
10. Diophantus's Arithmetica 93
11. The Great Art 109
12. Symbol Infancy 116
13. The Timid Symbol 127
14. Hierarchies of Dignity 133
15. Vowels and Consonants 141
16. The Explosion 150
17. A Catalogue of Symbols 160
18. The Symbol Master 165
19. The Last of the Magicians 169
Part 3 The Power of Symbols 177
20. Rendezvous in the Mind 179
21. The Good Symbol 189
22. Invisible Gorillas 192
23. Mental Pictures 210
24. Conclusion 216
Appendix A Leibniz's Notation 221
Appendix B Newton's Fluxion of xn 223
Appendix C Experiment 224
Appendix D Visualizing Complex Numbers 228
Appendix E Quaternions 230
Acknowledgments 233
Notes 235
Index 269
- Log in to post comments




