- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Geometrical Vectors

Publisher:
Chicago University Press
Publication Date:
1998
Number of Pages:
126
Format:
Paperback
Series:
Chicago Lectures in Physics
Price:
21.00
ISBN:
978-0226890487
Category:
General
[Reviewed by , on ]
Fernando Q. Gouvêa
02/11/1999
What is a vector? When we’re teaching calculus, a vector is an arrow on the plane or in three-dimensional space. In some books, vectors are “displacements” between points. In others, one is hard-pressed to see the difference between them and the points themselves. Then, in Linear Algebra, the points are vectors, and in fact “vector” comes to mean “any element of a vector space”, so that the word almost loses its specific meaning. But not completely: when we work in function spaces, we usually talk of “eigenfunctions”… perhaps because it just feels weird to call a function a vector.
Of course, down the hall, or on the other floor, in the Physics department, the story is very different. The question “what is a vector?” there seems to mean something more like “what sorts of quantities should we represent by vectors?” And the criterion has to do with the change of basis theorem: a vector (in R3) is something that is represented by three real numbers once a basis is chosen, but only if those real numbers transform themselves as expected when one changes the basis. From this standpoint, physicists talk of “contravariant vectors” (the usual ones), “covariant vectors” (elements of the dual vector space), and of even stranger beasts such as “contravariant vector densities”.
From the mathematical point of view, these gadgets might be understood in terms of the theory of differential forms, or, if one wants to be even more ethereal, in terms of tangent and cotangent bundles and their exterior powers. This becomes especially clear when one starts to talk of “vector fields”: a “covariant vector field”, for example, is what mathematicians would call a “differential form” (or, if various kinds of forms are to be considered, a “1-form”).
In this book, physicist Gabriel Weinreich constructs a different account of this theory, one that is fundamentally geometrical. He starts from the usual vectors (conceived of as arrows), but argues that a quantity should be represented by an arrow vector only if it transforms correctly under all topological transformations of the space. (I’m not sure he ever checks this, but he certainly considers all linear transformations.) From this point of view, certain things (for example, the electric field between two charged plates) are not arrow vectors, because scaling the space does not scale these quantities in the expected way.
Spurred on by this observation, Weinreich introduces a veritable zoo of objects that are “vector-like”. The first is the traditional arrow (though even this one is split into two kinds, arrows with orientation marked by an arrowhead and arrows with orientation marked by a preferred direction of rotation around them). The second is what he calls “stack vectors”, to be conceived as a stack of parallel planes together with a common choice of “up” for all the planes. Such an object clearly has a direction, and he defines its magnitude to be the density of the stack of planes along the perpendicular direction. There is clearly a way to translate such a stack vector to an arrow: take the arrow perpendicular to the family of parallel planes, of a length proportional to the density of the stack. But this identification is non-canonical, and Weinreich argues that the distinction between the two is important.
 It turns out that one is not allowed to compute the dot product of two arrows, nor of two stacks, but only of an arrow and a stack. The recipe for the computation of the dot product is again geometric (and has the curious property of making the dot product always be an integer… but remember that Weinreich is after a theory that is invariant under scaling). To the mathematician, this is the clue: “stack vectors” are elements of the vector space dual to the space of arrows.
It turns out that one is not allowed to compute the dot product of two arrows, nor of two stacks, but only of an arrow and a stack. The recipe for the computation of the dot product is again geometric (and has the curious property of making the dot product always be an integer… but remember that Weinreich is after a theory that is invariant under scaling). To the mathematician, this is the clue: “stack vectors” are elements of the vector space dual to the space of arrows.
Weinreich then considers the “cross product”, which leads him to further kinds of vectors. The cross product of two arrow vectors turns out to be a “thumbtack”, a kind of oriented area. The cross product of two stacks is a fourth kind of vector, “a sheaf”, to be thought of as a family of parallel lines in three-dimensional space. From a (pedantic) mathematical point of view, these seem to result from identifying the cross product with the wedge product of forms, so that “sheaves” are 2-forms and “thumbtacks” are their dual objects. Weinreich argues (implicitly) that all of these are really different things, and that we get away with treating them all as the same only because all of these spaces are three-dimensional. The choice of a basis for the space of arrows determines bases of the other spaces in a canonical way, and then all of them can be thought of as triples of coordinates.
Along the way, Weinreich runs into the fact that there are two ways of determining orientation. For example, arrows can be oriented by putting an arrowhead on them, but also by specifying a preferred direction of rotation around their axis. These are related by a “right hand rule”, but the “right hand rule” only makes sense after one has picked an orientation (otherwise, how would we know which is the right hand?). Since Weinreich wants everything to be invariant (at least!) under all sorts of linear transformations, he ends up deciding to keep the two sorts of orientation distinct, calling them “polar” and “axial”. Inevitably, he is led to consider scalars of both kinds too, “polar scalars” being real numbers, and “axial scalars” being something else which he never specifies (but which are suspiciously like pure imaginary numbers).
It’s all great fun, particularly for a mathematician who is willing to work out what the fancy mathematical way of making Weinreich’s distinctions would be. One is struck by the difference in spirit, here, between mathematics and (at least Weinreich’s type of) physics: mathematicians go for formalism and algebraic definitions, while physicists prefer pictures and intuition.
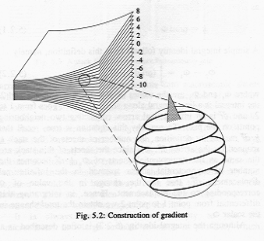 At times, it’s also illuminating. Consider, for example, how Weinreich defines the gradient of a scalar field (i.e., a function of three variables). He represents the scalar field as a collection of level surfaces in three-dimensional space. There is a natural orientation to these surfaces, at least locally: “up” is in the direction of larger values of the function. To compute the gradient, one takes a “melon baller” and scoops up a bit of this picture around a point. Locally, the surfaces all look like planes, so this is a stack of planes with an orientation: a stack vector! This stack vector is the gradient of the scalar field at that point. And notice that since the thing one does most often with the gradient is to compute its dot product with arrows (in order to get a directional derivative), making it a stack vector is just what we want. I was somewhat amazed that this gives the correct differential operator. In particular, I find it very nice that the limit process is hiding in the local linearization that’s implicit in the description.
At times, it’s also illuminating. Consider, for example, how Weinreich defines the gradient of a scalar field (i.e., a function of three variables). He represents the scalar field as a collection of level surfaces in three-dimensional space. There is a natural orientation to these surfaces, at least locally: “up” is in the direction of larger values of the function. To compute the gradient, one takes a “melon baller” and scoops up a bit of this picture around a point. Locally, the surfaces all look like planes, so this is a stack of planes with an orientation: a stack vector! This stack vector is the gradient of the scalar field at that point. And notice that since the thing one does most often with the gradient is to compute its dot product with arrows (in order to get a directional derivative), making it a stack vector is just what we want. I was somewhat amazed that this gives the correct differential operator. In particular, I find it very nice that the limit process is hiding in the local linearization that’s implicit in the description.
Weinreich goes on to do much more. At the right point in the book, he introduces the “real” names of his creatures, so that a “thumbtack”, for example, turns out to be a “covariant vector capacity”. (If nothing else, Weinreich has taught us better names for things.) He then considers scalar and vector fields, defines the divergence and the curl, and “proves” the standard theorems. Finally, in a chapter called “Goodbye to the Rubber Universe”, he goes back to geometry, restricts his transformations to isometries, and recaptures much of the traditional theory.
This book is lots of fun. Any math book with a section entitled “Hermaphrodite Sense Gender of the Bases” is bound to be at least interesting. This one is both interesting and illuminating. I probably won’t adopt Weinreich’s language anytime soon, but I’m glad I’ve read his book.
Fernando Q. Gouvêa is associate professor of mathematics at Colby College, editor of MAA Online, and much too busy.
Preface
1: Prologue: What This Book Is About
2: Vector Types and Vector Operations
3: More Operations, More Vectors
4: Completion of the Menagerie
5: Fields and the Geometrical Calculus
6: Coordinates and Components
7: The Grand Algebraization Rule
8: Goodbye to the Rubber Universe
9: Epilogue: Where This Book Leaves Us
Index
- Log in to post comments




