- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mrs. Perkins's Electric Quilt

Publisher:
Princeton University Press
Publication Date:
2009
Number of Pages:
391
Format:
Hardcover
Price:
29.95
ISBN:
9780691135403
Category:
General
The Basic Library List Committee suggests that undergraduate mathematics libraries consider this book for acquisition.
[Reviewed by , on ]
Henry Ricardo
10/18/2009
I’ll need a larger thesaurus if I review any more books by Paul Nahin. Once again, he has written a gem of a book, this time a series of “discussions” of various ways in which mathematics and physics are “mutually dependent and mutually illuminating.” The author refers to this as the “mutual embrace.”
The press release from Princeton University Press refers to the author as a “best-selling pop-math author,” but Nahin’s books are not “mathematics for the masses.” Reading MPEQ with comprehension requires a solid understanding of mathematics and physics at the level of a first year science or engineering major at a good college or university. For example, in the Preface, the author poses the problem of showing that
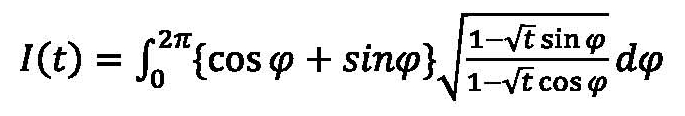
is not zero for t in [0,1]. In total, there are thirty-five such Challenge Problems sprinkled throughout the book.
The Table of Contents reveals the breadth of Nahin’s discussions: Newtonian gravity, air drag, electrical engineering, Fourier series, the zeta function, and probability (both theoretical and Monte Carlo simulation). He provides helpful MATLAB code at various points of the book.
Chapter 13 (“Quilts & Electricity”) does not deal with thermal efficiency on a cold winter’s night. Rather, the author starts with a recreational problem popularized by Sam Loyd and later reproduced and given the name Mrs. Perkins’s Quilt by Henry Dudeney: A square quilt of 169 identical square patches is to be cut into a number of pieces which are themselves square by cutting along the stitch lines (i.e., no cutting through a patch). How can this be done in the fewest number of subsquares? Nahin traces generalizations of this problem up to the 1936-1938 joint work of four undergraduates at Trinity College, Cambridge, including William Tutte (then a chemistry major, eventually a distinguished professor of mathematics in Canada). These young men discovered a completely unexpected, intimate connection between the dissection problem and electrical circuit theory. Nahin illuminates this connection and comments (with a journal reference) that one application of the mathematical problem is the determination of the “best” way to place electronic circuitry on microchips.
Written in Nahin’s usual informal and humorous style (but with admirable rigor when appropriate), Mrs. Perkins’s Electric Quilt will delight all but the “absolutely pure experimentalists, covered with vacuum pump grease and proud of it,…and absolutely pure mathematicians, e.g., those who lust only for a one-page analytical proof of the four-color theorem, or of Fermat’s Last Theorem…” I suspect that even some of these extremists will be captivated by Paul Nahin’s wit and wisdom.
Henry Ricardo (henry@mec.cuny.edu) has retired from Medgar Evers College (CUNY) as Professor of Mathematics, but continues to serve as Governor of the Metropolitan NY Section of the MAA. He is the author of A Modern Introduction to Differential Equations (Second Edition). His linear algebra text will be published in October by CRC Press.
For the Reader xi
Preface xiii
Chapter 1: Three Examples of the Mutual Embrace 1
1.1 Unphysical Laws 1
1.2 When Math Goes Wrong 6
1.3 Math from Physics 13
Chapter 2: Measuring Gravity 18
2.1 First, a Little Theory 18
2.2 Out in the Author's Garage 21
Chapter 3: Feynman's Infinite Circuit 24
3.1 An Infinity of Resistors 24
3.2 An Infinity of Reactances, and
Recursion 27
3.3 Convergence--or Not? 32
3.4 Three More Infinite, All-Resistor
Networks 36
Chapter 4: Air Drag--A Mathematical View 44
4.1 Air Drag Treated Broadly 44
4.2 Air Drag Treated with Some Detail 51
Chapter 5: Air Drag--A Physical View 62
5.1 The Quadratic Force Law 62
5.2 Long Falls through a Real Atmosphere 70
Chapter 6: Really Long Falls 82
6.1 Falling into the Sun 82
6.2 Falling from Heaven to Hell 86
Chapter 7: The Zeta Function--and Physics 94
7.1 A Curious Double Integral 94
7.2 Fourier Series and the Zeta Function 95
7.3 The Zeta Function in Physics 100
Chapter 8: Ballistics--With No Air Drag (Yet) 107
8.1 Shooting a Cannon in a Vacuum 107
8.2 What Makes a Champion Shot-Putter? 112
8.3 Another Cannon Question 116
Chapter 9: Ballistics--With Air Drag 120
9.1 Thin Air Cannot Be Ignored! 120
9.2 Air Drag and Baseball 126
Chapter 10: Gravity and Newton 136
10.1 The Beginnings of Modern Gravity 136
10.2 Newton's Superb Theorems 140
10.3 The Moon Test and Blowing-Up Planets 148
10.4 A Surprising Gravity Calculation 152
10.5 Gravitational Contraction 157
Chapter 11: Gravity Far Above the Earth 170
11.1 Kepler's Laws of Planetary Motion 170
11.2 Weighing the Planets 175
Chapter 12: Gravity Inside the Earth 186
12.1 Newton's Experiment 186
12.2 Gravity Inside the Earth 191
12.3 Pressure at the Center of the Earth 200
12.4 Travel Inside the Earth 203
12.5 Epilogue 209
Chapter 13: Quilts & Electricity 215
13.1 Recreational Mathematics 215
13.2 Electric Quilts 220
13.3 Three Impossibility Proofs 225
Chapter 14: Random Walks 233
14.1 Ronald Ross and the Flight of Mosquitoes 233
14.2 Karl Pearson Formulates a Famous Problem 236
14.3 Gambler's Ruin 241
14.4 The Monte Carlo Method 245
Chapter 15: Two More Random Walks 261
15.1 Brownian Motion 261
15.2 Shrinking Walks 269
Chapter 16: Nearest Neighbors 285
16.1 Cannibals Can Be Fun! 285
16.2 Neighbors Beyond the Nearest 291
16.3 What Happens When We Have Lots
of Cannibals 294
16.4 Serious Physics 296
Chapter 17: One Last Random Walk 299
17.1 Resistor Mathematics 299
17.2 Electric Walks 301
17.3 Monte Carlo Circuit Simulation 305
17.4 Symmetry, Superposition, and Resistor Circuits 313
Chapter 18: The Big Noise 321
18.1 An Interesting Textbook Problem 321
18.2 The Polar Equations of the Big-Noise Flight 322
18.3 The Acceleration on a Big-Noise Flight Path 328
SOLUTIONS TO THE CHALLENGE PROBLEMS 333
SPECIAL BONUS DISCUSSION 371
Warning: Do Not Read before Reading Disscussion 17 373
Chapter 19: Electricity in the Fourth Dimension 373
19.1 The Tesseract 373
19.2 Connecting a Tesseract Resistor Cube 376
Acknowledgments 385
Index 387
- Log in to post comments




