- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Rules of Algebra (Ars Magna)

Publisher:
Dover Publications
Publication Date:
1968
Number of Pages:
267
Format:
Paperback
Price:
14.95
ISBN:
9780486458731
Category:
Monograph
The Basic Library List Committee recommends this book for acquisition by undergraduate mathematics libraries.
[Reviewed by , on ]
Richard J. Wilders
07/16/2010
Ars Magna was published in 1545 within two years of Copernicus’ On the Revolutions of the Heavenly Spheres. Of even greater interest, Ars Magna is dedicated to Andreas Osiander who wrote the famous introduction to Copernicus’ treatise. Cardano was a fascinating character, who describes himself as an “Outstanding Mathematician, Philosopher, and Physician” and the text itself as being part of what he called “The Perfect Work.” His interactions with contemporaries from his native Italy make for wonderful reading independent of the mathematics involved. Cardano was also an alchemist, as were many of his peers. The edition reviewed here is a 2007 Dover reprint of the 1968 MIT Press translation. Footnotes detail any changes made in the several later editions of this important work.
Ars Magna is concerned with the solution of polynomial equations. Its most important results, from an historical point of view, are the solutions he offers for what we now refer to as the cubic and quartic equations. While the Dover edition uses modern notation, the techniques used are decidedly not modern. For historians of mathematics and for those who teach its history Ars Magna is definitely required reading. It provides a glimpse into the tortured ways mathematicians had to proceed prior to arriving at the notion of a general polynomial with arbitrary coefficients. Deciphering a page or two of Ars Magna would make a nice project for an undergraduate student in a history of mathematics course.
At the time Cardano wrote Ars Magna, x3 + 3x = 7 and x3 – 3x = 7 were treated as different problems; the latter equation was written as x3 = 3x + 7. These two problems are treated in chapters titled respectively “On the Cube and First Power Equal to the Number, Generally” and “On the Cube Equal to the Number and the First Power, Generally.” Additionally, polynomials with missing terms were not treated as having a coefficient of 0 but as entirely separate cases. Pages 24-26 provide a complete catalog of the various cases Cardano must consider. It is thus not appropriate to say that Cardano solved the cubic equation — he saw not one but many equations where we now see one. Nonetheless, his techniques are perfectly general.
Cardano’s treatment of the solutions he finds is also very different from the modern approach and betrays his Euclidean view of the number concept: a single number represents a length, the product of two numbers an area. While Cardano deals with complex numbers in an appropriate fashion when he encounters them, he refers to real solutions as true or fictitious according as to whether they are positive or negative. He begins Ars Magna with a discussion regarding the determination of the number of “true” and “fictitious” solutions the various polynomial equations he considers can have. As an example of his technique we consider his treatment of equations of the form x3 + a = bx. By assumption, both a and b are positive. Cardano informs us that we can determine the number of true and fictitious roots as follows:
“…see whether multiplying two-thirds the coefficient of the first power by the square root of one-third the same yields the constant or something greater or lesser. If the product and the constant are precisely the same, the unknown has two values, and one of the two is true, namely the same square root which has been multiplied … [I]f the product … is greater than the constant, there will be three solutions, two that are true and a third that is false … [I]f the product… is less than the given constant, there will be no true solutions but a fictitious one.” (Pages 11–13)
No explanation is given, although examples of each case are provided. From a modern perspective, it’s possible to see what Cardano is doing. The polynomial x3 + a = bx has a minimum at the square root of b/3 and a maximum at the negative square root.. Its minimum value is precisely the constant (a) minus the product he describes. Thus, if the product equals the constant the minimum is a double root and the polynomial has one true root. If the product is greater than the constant the minimum is less than 0 and there are two “true” roots. If the product is less than the constant the minimum is greater than 0 and there are no true roots and one fictitious one.
While Cardano finds his solutions using algebraic techniques which are still used today his proofs are all geometric in the style of Euclid. In Chapter V he demonstrates the solution to x2 + 6x = 91 by drawing a square with sides of length x, appending 3-by-x rectangles on two adjacent sides and then completing the square with a square with sides 3. The result is x2 + 6x + 9 = 91 + 9 = 100 or (x + 3)2 = 100, of which the “true” root is 7.
Cardano clearly has general solutions for the various forms of the quadratic but does not write them out in explicit form. His description (page 43) of the solution to x2 + 2x = 12 – √44 is entirely in prose. Lest you think this problem a bit contrived, Cardano has an answer for you: “teachers ought always to teach their poor pupils a certain number of minutiae very thoroughly…” (Page 43). Try that one out the next time a student asks the ever-popular question “What’s this good for?”
In Chapter XI we encounter the equation (x3 + px = q) that instigated the well-known feud between Cardano and Niccolo Tartaglia. Although Cardano credits Tartaglia (page 96) with the solution (though not with the demonstration) Tartaglia felt betrayed and challenged Cardano to a “math duel” in which the contestants compete to solve mathematics problems. You can read more about this in the fine introduction to the current edition. Cardano begins his exposition with a geometric demonstration of the solution he will describe rhetorically. He tells us (in rhetorical fashion) to construct the binomium
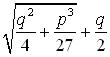
and the apotome
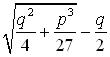
He then informs us that the required root is the difference of the cube roots of these two expressions. While Cardano considers only a specific example, his method is quite general. For more on Cardano and his solution to this particular class of cubic there is probably no better source than William Dunham’s Journey Through Genius, which provides a nice biography as well as an explication of Cardano’s reasoning process.
Chapters XII through XXIII provide solutions to the multiple other cases of the cubic he is forced to deal with including those cases in which x2 appears. His technique is equivalent to the modern substitution which eliminates the term in x2 to create the reduced cubic, but he needs to deal with multiple cases because of the prohibition against negative coefficients. As a result the substitution technique occupies most of Chapter VII: The Transformation of Equations.
In Chapter XXXIX we meet the quartic equation whose solution Cardano properly credits to Lodovico Ferrari. Page 237 contains a list of 20 of the 87 different versions of the quartic he deals with. His first example is a problem he attributes to Zuanne de Tonini da Coi:
“…divide 10 into three proportional parts, the product of the first and second of which is 6.” (Page 239)
To solve this problem we must find numbers in continued proportion which sum to 10 and such that the product of the first and second of the numbers is 6. If we let x be the second number (the mean in Cardano’s terms), then the first is 6/x and it follows that c = x3/6. This yields the quartic 60x = x4 + 6x2 + 36. Cardano then proceeds to add 6x2 to both sides obtaining x4 + 12x2 + 36 = 6x2 + 60x, which has a perfect square on the left side. He then proceeds to find an expression in an auxiliary variable b which when added to both sides results in a perfect square on both sides of the equation. This problem results in a cubic equation in b (now known as the resolvent cubic) which Cardano knows how to solve. Once this is accomplished all four solutions are obtained by taking the (positive and negative) square roots of both sides of the new quartic.
Unlike the examples we encounter in history of mathematics texts, the value Cardano obtains for b in this example does not simplify to a whole number or simple radical. As a result the subsequent calculations are quit tedious. He omits the final solution and concludes his discussion with the 16th century’s version of “the proof is left to the exercises”: “Follow, then, Chapter V on the square and number equal to the first power…You will then have x” (page 243). I used Maple and found two “true” solutions: x ≈ .644, x ≈ 3.099.
Cardano, never accused of being overly humble, ends his work with the following bit of seeming braggadocio:
WRITTEN IN FIVE YEARS, MAY IT LAST
AS MANY THOUSANDS
THE END OF THE GREAT ART ON
THE RULES OF ALGEBRA
BY GIROLAMO CARDANO
(Page 261, caps in original.) While we can’t be sure, it seems likely his prediction will turn out to be correct. At any rate, I would heartily recommend that anyone interested in algebra or its history have a copy of this wonderful little book in their library. High school and college libraries should also have a copy.
Richard Wilders is Marie and Bernice Gantzert Professor in the Liberal Arts and Sciences and Professor of Mathematics at North Central College. His primary areas of interest are the history and philosophy of mathematics and of science. He has been a member of the Illinois Section of the Mathematical Association of America for 30 years and is a recipient of its Distinguished Service Award. His email address is rjwilders@noctrl.edu.
| Foreword by Oystein Ore | |||||||
| Preface | |||||||
| The Great Art, or The Rules of Algebra by Girolamo Cardano | |||||||
| Appendix: Portions of Euclid's Elements Cited by Cardano | |||||||
| Index |
- Log in to post comments




