- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
American Mathematical Monthly -August-September 2010
![]()
August/September 2010
Symmetrically Bordered Surfaces
By: William Cavendish and John H. Conway
wcavendi@math.princeton.edu, jhorcon@yahoo.com
We address the question: given a compact topological surface with boundary, when can it be symmetrically embedded in  We construct examples of symmetric embeddings for compact surfaces with an odd number of boundary components, and connected sums of an even number of â„â„™2 ’s (cross surfaces) with any number of boundary components. We show in the appendix that a connected sum of an odd number of â„â„™2 ’s with 4n boundaries cannot be symmetrically embedded.
We construct examples of symmetric embeddings for compact surfaces with an odd number of boundary components, and connected sums of an even number of â„â„™2 ’s (cross surfaces) with any number of boundary components. We show in the appendix that a connected sum of an odd number of â„â„™2 ’s with 4n boundaries cannot be symmetrically embedded.
Stern's Diatomic Sequence 0, 1, 1, 2, 1, 3, 2, 3, 1, 4, Â…
By: Sam Northshield
northssw@plattsburgh.edu
Stern’s diatomic sequence is a simply defined sequence with an amazing set of properties. It appeared in print in 1858 and has been the subject of numerous papers since. Our goal is to present many of these properties, both old and new. We present a large set of references and, for many properties, we supply simple proofs or ones that complement existing proofs. Among the topics covered are what these numbers count (hyperbinary representations) and the sequence’s surprising parallels with the Fibonacci numbers. Quotients of consecutive terms lead to an enumeration of the rationals. Other quotients lead to a map from dyadic rationals to the rationals whose completion is the inverse of Minkowski’s ? function. Along the way, we get a distant view of fractals and the Riemann hypothesis as well as foray into random walks on graphs in the hyperbolic plane.
Dispersive Quantization
By: Peter J. Oliver
olver@math.umn.edu
The evolution, through linear dispersion, of piecewise constant periodic initial data leads to surprising quantized structures at rational times, and fractal, nondifferentiable profiles at irrational times. Similar phenomena have been observed in optics and quantum mechanics, and lead to intriguing connections with exponential sums arising in number theory. Ramifications of these observations for numerics and nonlinear dispersion are proposed as open problems.
A Fancy Way to Obtain the Binary Digits of 759250125 
By: Thomas Stoll
tstoll@cs.uwaterloo.ca
R. L. Graham and H. O. Pollak observed that the sequence
 has the curious property that the sequence of numbers
has the curious property that the sequence of numbers  gives the binary digits of
gives the binary digits of  . We present an extension of the Graham–Pollak sequence which allows us to get—in a fancy way—the binary digits of 759250125
. We present an extension of the Graham–Pollak sequence which allows us to get—in a fancy way—the binary digits of 759250125 s and other numbers.
s and other numbers.
Wallis-Ramanujan-Schur-Feynman
By: T. Amdeberhan, O. R. Espinosa, V. H. Moll, and A. Straub
tamdeberhan@math.tulane.edu, olivier.espinosa@usm.cl, vhm@math.tulane.edu, astraub@math.tulane.edu
One of the earliest examples of analytic representations for is given by an infinite product provided by Wallis in 1655. The modern literature often presents this evaluation based on the integral formula
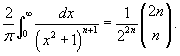
In trying to understand the behavior of this integral when the integrand is replaced by the inverse of a product of distinct quadratic factors, the authors encounter relations to some formulas of Ramanujan, expressions involving Schur functions, and Matsubara sums that have appeared in the context of Feynman diagrams.
Notes
On Cantor's First Uncountability Proof, Pick’s Theorem, and the Irrationality of the Golden Ratio
By: Mike Krebs and Thomas Wright
mkrebs@calstatela.edu, wright@math.jhu.edu
In Cantor’s original proof of the uncountability of the reals (not the diagonalization argument), he constructs, given any countable sequence of real numbers, a real number not in the sequence. When we apply this argument to a certain standard enumeration of the rationals, the real number we produce will necessarily be irrational. Using some planar geometry, including Pick’s theorem on the number of lattice points enclosed within certain polygonal regions, we show that this number is the reciprocal of the golden ratio, whence follows the well-known fact that the golden ratio is irrational.
The Diophantine Equation  in Gaussian Integers
in Gaussian Integers
By: Filip Najman
fnajman@math.hr
In this note we find all the solutions of the Diophantine equation  using elliptic curves over â„š (i) . Also, using the same method we give a new proof of Hilbert's result that the equation
using elliptic curves over â„š (i) . Also, using the same method we give a new proof of Hilbert's result that the equation  has only trivial solutions in Gaussian integers.
has only trivial solutions in Gaussian integers.
Polynomial Root Motion
By: Christopher Frayer and James A. Swenson
frayerc@uwplatt.edu, swensonj@uwplatt.edu
A polynomial is determined by its roots and its leading coefficient. If you set the roots in motion, the critical points will move too. Using only tools from the undergraduate curriculum, we find an inverse square law that determines the velocities of the critical points in terms of the positions and velocities of the roots. As corollaries we get the Polynomial Root Dragging Theorem and the Polynomial Root Squeezing Theorem.
From Enmity to Amity
By: Aviezri S. Fraenkel
fraenkel@wisdom.weizmann.ac.il
Sloane’s influential On-Line Encyclopedia of Integer Sequences is an indispensable research tool in the service of the mathematical community. The sequence A001611 listing the "Fibonacci numbers + 1" contains a very large number of references and links. The sequence A000071 for the "Fibonacci numbers 1" contains an even larger number. Strangely, resentment seems to prevail between the two sequences; they do not acknowledge each other’s existence, though both stem from the Fibonacci numbers. Using an elegant result of Kimberling, we prove a theorem that links the two sequences amicably. We relate the theorem to a result about iterations of the floor function, which introduces a new game.
Reviews
Finite Group Theory
By: I. Martin Isaacs
Reviewed by: Peter Sin
sin@math.ufl.edu





