- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
American Mathematical Monthly -October 2010
![]()
November 2010
Teaching Research: Encouraging Discoveries
By: Francis Edward Su
su@math.hmc.edu
What does it take to turn a learner into a discoverer? Or to turn a teacher into a co-adventurer? A handful of experiences—from teaching a middle-school math class to doing research with undergraduates—have changed the way that I would answer these questions. Some of the lessons I've learned have surprised me.
Julius and Julia: Mastering the Art of the Schwarz Lemma
By: Harold P. Boas
boas@tamu.edu
This article discusses classical versions of the Schwarz lemma at the boundary of the unit disk in the complex plane. The exposition includes commentary on the history, the mathematics, and the applications.
Fermat’s Spiral and the Line Between Yin and Yang
By: Taras Banakh, Oleg Verbitsky, and Yaroslav Vorobets
tbanakh@yahoo.com, verbitsky@informatik.hu-berlin.de , yvorobet@math.tamu.edu
Let D denote a disk of unit area. We call a set ![]() perfect if it has measure 1/2 and, with respect to any reflection symmetry of D, the maximal symmetric subset of A has measure 1/4. We call a curve
perfect if it has measure 1/2 and, with respect to any reflection symmetry of D, the maximal symmetric subset of A has measure 1/4. We call a curve ![]() in D a yin-yang line if
in D a yin-yang line if
-
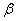 splits D into two congruent perfect sets,
splits D into two congruent perfect sets, -
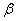 crosses each concentric circle of D twice,
crosses each concentric circle of D twice, -
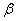 crosses each radius of D once.
crosses each radius of D once.
We prove that Fermat’s spiral is the unique yin-yang line in the class of smooth curves
algebraic in polar coordinates.
Analysis with Ultrasmall Numbers
By: Karel Hrbacek, Olivier Lessmann, and Richard O’Donovan
khrbacek@sci.ccny.cuny.edu,, olivier.lessmann@edu.ge.ch , richard.o-donovan@edu.ge.ch
We develop a context-based theory of ultrasmall (infinitesimal) and ultralarge real numbers from a few simple principles, and present some examples of their use in analysis. In this theory, perhaps for the first time, definitions and arguments involving infinitesimals can be presented in a style that is both as informal and as rigorous as is customary in standard textbooks of real analysis.
Notes
Irreducible Cubics Modulo Five
By: Hendrik Lenstra
Finite fields are finite, and they are fields, and as a result one can combine algebraic arguments with counting arguments in their study. This was illustrated in a lecture given at the 2009 April Fools’ meeting of the Leiden bachelor seminar. Here is the text of that lecture.
A Short Proof of Combinatorial Nullstellensatz
By: Mateusz Michałek
mateusz.michalek@ujf-grenoble.fr
In this note we give a short, direct proof of the combinatorial Nullstellensatz.
A Continuous Bijection from ![]() onto a Subset of
onto a Subset of ![]() Whose Inverse Is Everywhere Discontinuous
Whose Inverse Is Everywhere Discontinuous
By: Sam H. Creswell
screswell@alamo.edu
There is a continuous bijection from ![]() onto a subset of
onto a subset of ![]() whose inverse is everywhere discontinuous.
whose inverse is everywhere discontinuous.
On a Question of Connes and Zagier Regarding Parallelograms Inscribed in a Pair of Confocal Ellipses
By: Nicolae Anghel
anghel@unt.edu
It is shown that a pair of nested concentric ovals has the property that each point on either one of the ovals is a vertex of exactly one inscribed parallelogram of maximal perimeter if and only if the joint Monge orthoptic curve of the ovals is a circle. This gives an answer to a question posed by Connes and Zagier in the note A property of parallelograms inscribed in ellipses, which appeared in the American Mathematical Monthly in 2007.
A Streamlined Proof of an Essential Calculus Fact
By: Stephen M. Walk
smwalk@stcloudstate.edu
We present a short, classroom-friendly proof of a standard theorem of calculus: continuity on an interval implies Riemann-integrability on that interval. Reviews
Statistical Models: Theory and Practice (Revised Edition).
By: David A. Freedman
Reviewed by: Rebecca F. Goldin
rgoldin@math.gmu.edu





