American Mathematical Monthly - October 2016

October does not just mean frost on the pumpkin, but the best in Mathematics. We open the October Monthly with our annual review of the William Lowell Putnam Mathematical Competition. Read onward to get a status report on the current state of the 3x+1 Problem ​in Jeffrey Lagarias' "Erdős, Klarner, and the 3x + 1 Problem." And if this is not enough, we feature former Monthly Editor and Ford-Halmos Award winning author Dan Vellemen who co-authors "Anonymity in Predicting the Future​​." Mark Kidwell reviews "Knots, Molecules, and the Universe: An Introduction to Topology" by Eric Flapan, and our Problem Section is all treats with no tricks. Stay tuned for the November Monthly when we open with a tribute to the late Jonathan Borwein.

  - Scott T. Chapman, Editor

JOURNAL SUBSCRIBERS AND MAA MEMBERS:

To read the full articles, please log in to the member portal by clicking on 'Login' in the upper right corner. Once logged in, click on 'My Profile' in the upper right corner.

Table of Contents

The Seventy-Sixth William Lowell Putnam Mathematical Competition

Leonard F. Klosinski, Gerald L. Alexanderson and Mark Krusemeyer

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.739

Erdős, Klarner, and the 3x + 1 Problem

Jeffrey C. Lagarias

This paper describes work of Erdős, Klarner, and Rado on semigroups of integer affine maps and on sets of integers they generate. It gives the history of problems they studied, some solutions, and new unsolved problems that arose from them.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.753

Anonymity in Predicting the Future

Dvij Bajpai and Daniel J. Velleman

Consider an arbitrary set S and an arbitrary function f : ℝ → S. We think of the domain of f as representing time, and for each x ∈ ℝ, we think of f(x) as the state of some system at time x. Imagine that, at each time x, there is an agent who can see the values of f on (−∞, x) and is trying to guess f(x)—in other words, the agent is trying to guess the present state of the system from its past history. In a 2008 paper, Christopher Hardin and Alan Taylor use the axiom of choice to construct a strategy that the agents can use to guarantee that, for every function f, all but countably many of them will guess correctly. In a 2013 monograph, they introduce the idea of anonymous guessing strategies, in which the agents can see the past but don't know where they are located in time. In this paper, we consider a number of variations on anonymity. For instance, what if, in addition to not knowing where they are located in time, agents also do not know the rate at which time is progressing? What if they have no sense of how much time elapses between any two events? We show that in some cases agents can still guess successfully, while in others they perform very poorly.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.777

Equilateral Triangles and the Fano Plane

Philippe Caldero and Jérôme Germoni

We formulate a definition of equilateral triangles in the complex line that makes sense over the field with seven elements. Adjacency of these abstract triangles gives rise to the Heawood graph, which is a way to encode the Fano plane. Through some reformulation, this gives a geometric construction of the Steiner systems S(2,3,7) and S(3,4,8). As a consequence, we embed the Heawood graph in a torus, and we derive the exceptional isomorphism PSL₂(₇)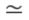GL₃(₂). The study of equilateral triangles over other finite fields shows that seven is very specific.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.789

The Art Gallery Theorem, Revisited

T. S. Michael and Val Pinciu

The art gallery theorem asserts that any polygon with n vertices can be protected by at most ⌊n/3⌋ stationary guards. The original proof by Chvátal uses a nonroutine and nonintuitive induction. We give a simple inductive proof of a new, more general result, the constrained art gallery theorem: If V* and E* are specified sets of vertices and edges that must contain guards, then the polygon can be protected by at most ⌊(n + 2|V*| + |E*|)/3⌋ guards. Our result reduces to Chvátal's art gallery theorem when V* and E* are empty. We give a second short proof of this generalization in the spirit of Fisk's proof of the art gallery theorem using graph colorings.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.802

Abelian and Non-Abelian Triangle Mysteries

Lon Mitchell, Michael A. Jones and Brittany Shelton

Behrends and Humble characterized the Abelian groups behind mysterious behavior related to certain triangular arrays and asked if such triangles could be constructed from non-Abelian groups. We show that commutativity plays an essential role in quasigroup and semigroup triangle mysteries and prove that “mysterious groups” must be Abelian.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.808

Notes

The Adventitious Angles Problem: The Lonely Fractional Derived Angle

Yong Kong and Shaowei Zhang

In the “classical” adventitious angle problem, for a given set of three angles a, b, and c measured in integral degrees in an isosceles triangle, a fourth angle θ (the derived angle), also measured in integral degrees, is sought. We generalize the problem to find θ in fractional degrees. We show that the triplet (a, b, c) = (45°, 45°, 15°) is the only combination that leads to θ = 7½° as the fractional derived angle.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.814

Maximal Isoptic Chords of Convex Curves

J. Jerónimo-Castro and C. Yee-Romero

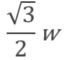
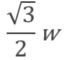
In this short note, we prove the following: for every convex body K in the plane of minimal width w, there exists a chord [x, y] with length larger than or equal to  such that there are support lines of K through x and y which form an angle π/3. Moreover, if there is not such a chord with length exceeding , then K is a Euclidean disc.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.817

An Alternate Derivation of the Euler–Poisson Equation

Olivier de La Grandville

Few equations are as simple looking and at the same time devoid of any apparent interpretation as the Euler–Poisson equation. We offer here a simple derivation—necessitating only elementary operations—that helps bring its meaning into full light.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.821

Variations on Barbălat's Lemma

Bálint Farkas and Sven-Ake Wegner

It is not hard to prove that a uniformly continuous real function, whose integral up to infinity exists, vanishes at infinity, and it is probably little known that this statement runs under the name “Barbălat's lemma.” In fact, the latter name is frequently used in control theory, where the lemma is used to obtain Lyapunov-like stability theorems for nonlinear and nonautonomous systems. Barbălat's lemma is qualitative in the sense that it asserts that a function has certain properties, here convergence to zero. Such qualitative statements can typically be proved by “soft analysis,” such as indirect proofs. Indeed, in the original 1959 paper by Barbălat, the lemma was proved by contradiction, and this proof prevails in the control theory textbooks. In this short note, we first give a direct, “hard analysis” proof of the lemma, yielding quantitative results, i.e., rates of convergence to zero. This proof allows also for immediate generalizations. Finally, we unify three different versions that recently appeared and discuss their relation to the original lemma.

DOI: http://dx.doi.org/10.4169/amer.math.monthly.123.8.825

Problems and Solutions

To purchase the article from JSTOR: http://dx.doi.org/10.4169/amer.math.monthly.123.8.831

Book Review

Knots, Molecules, and the Universe: An Introduction to Topology by Erica Flapan

Reviewed by Mark Kidwell

To purchase the article from JSTOR: http://dx.doi.org/10.4169/amer.math.monthly.123.8.840

MathBits

Yet Another Analytic Proof of Napoleon’s Theorem

Edited by J. A. Grzesik

A Physical Proof for Cauchy’s Inequality

Edited by Halil Mutuk