- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
A Modern Vision of the Work of Cardano and Ferrari on Quartics - Decimal Numbers Come to the Rescue
The first paragraph of Problem V states that "For example, divide 10 into three proportional parts, the product of the first and second of which is 6. This was proposed by Zuanne de Tonini da Coi, who said it would not be solved. I said it could, though I did not yet know the method [for doing so]. This was discovered by Ferrari." Cardano claims that the three numbers are 6/x, x, and x3/6. This makes sense because (6/x)x = 6, while the constant of proportionality is x/(6/x), that is to say x2/6. The third term will be x(x2/6). Since the sum of the three terms has to be 10, it follows that 6/x + x + x3/6 = 10, which in turn leads to x4 + 6x2 + 36 = 60x.
Problem V is the first instance in chapter 39 of Ars Magna where Cardano has to solve a quartic. Before doing so, he presents an elaborate geometrical proof that justifies the algebraic identity (s + a + b)2=(s + a)2 + 2bs + 2ab + b2 ([1], p. 238; [8], p. 57). Making s = x2 and a = 6, we get (x2 + 6 + b)2 = (x2 + 6)2 + 2bx2 + 12b + b2. But problem V is equivalent to x4 + 12x2 + 36= 6x2 + 60x, thus (x2 + 6)2 = 6x2 + 60x; therefore (x2 + 6 + b)2 = (2b + 6)x2 + 60x + (b2 + 12b). The right side will be a perfect square provided that the discriminant is zero, consequently 0 = 3600- 4(2b + 6)(b2 + 12b), i.e. b3 + 15b2 + 36b = 450. The usual method for solving cubics leads to a solution $$b_1= oot 3of {190+sqrt{33,903}}+ oot 3of {190-sqrt{33,903}} - 5;$$ thus, (x2 + 6 + b1)2 = (2b1 + 6)(x + 60/(2(2b1+6)))2. Finally $$(x^2+b_1+6)^2 = left(sqrt{2b_1+6}left(x + {30over 2b_1+6} ight) ight)^2,$$ which in turn leads to $$x^2+b_1+6 = pm left(xsqrt{2b_1+6} = {30oversqrt{2b_1+6}} ight).$$ The problem has been reduced to the task of solving two quadratic equations. We could write the equations in full once we note that $$b_1+6 = oot 3of{190+sqrt{33,903}} + oot 3of{190-sqrt{33,903}} + 1 quad { m and} quad 2b_1+6 = oot 3of {1,520 + sqrt{2,169,792}} + oot 3of {1,520 - sqrt{2,169,792}} - 4.$$
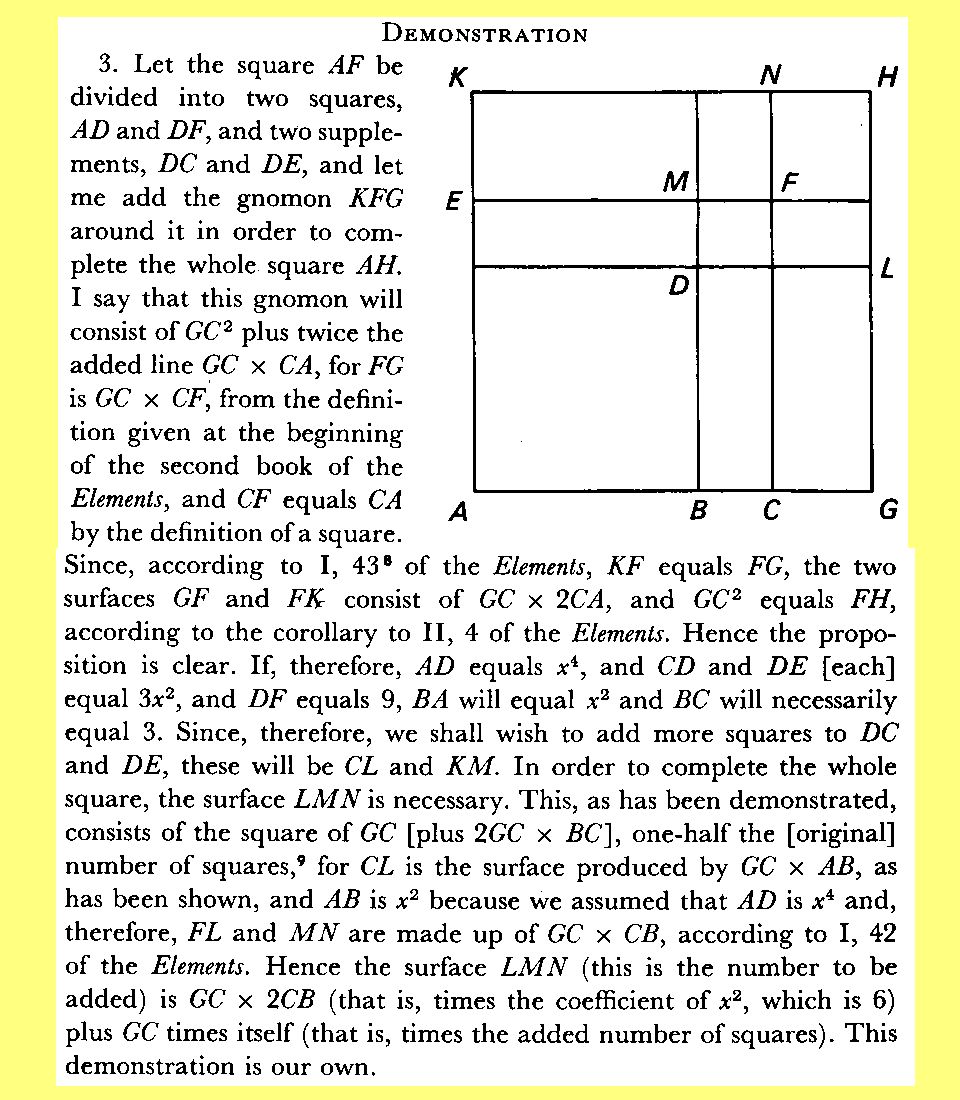
Figure 4: Cardano's geometrical proof related to problem V of chapter 39
Although as early as the 12th century Islamic mathematicians used decimals for the purpose of approximation ([7], p. 270), decimal approximations of irrational numbers were not used in Europe when Ars Magna was published for the first time. No wonder that decimals are nowhere to be found in Cardano's masterpiece; througout chapter 39 exact solutions are sought.
Decimals are very handy when discussing Problem V: Using the decimal approximation 4.00979 to b1 we would have to solve, for instance, the quadratic equation $$x^2+4.00979 +6 = xsqrt{2cdot 4.00979+6} + {30over sqrt{2cdot 4.00979+6}}.$$ The solutions of it are, approximately, 3.09987 and 0.644398.
An alternative approach to the solution of x4 + 6x2 + 36 = 60x is to introduce a new variable z and note that (x2 + z)2 = (2z - 6)x2 + 60x + z2 - 36. In order to have a perfect square we need to solve the equation 602 - 4(2z - 6)(z2 - 36) = 0, i.e. z3 - 3z2 - 36z - 342 = 0. The transformation y = z - 1 leads to y3 = 39y + 380, whose solution is $$y = oot 3of{190+3sqrt{3,767}} + oot 3of{190-3sqrt{3,767}}.$$ Therefore z » 10.0098. The problem is then reduced to the solution of the equation $$ (x^2+10.0098)^2 = (2cdot 10.098-6)left(x+{60over 2(2cdot 10.098-6)} ight)^2.$$ Thus, $$x^2+10.098 = sqrt{28.0392}left(x+{60over 28.0392} ight) quad { m or} quad x^2+10.0098= -sqrt{28.0392}left(x+{60over 28.0392} ight).$$ The first quadratic has the real solutions 3.09988 and 0.644399 while the second provides two complex solutions. The whole problem looks quite simple, but let us keep in mind that we are using decimal approximations! They have helped us to focus on the method by allowing us to avoid complicated expressions.
Harald Helfgott (University of Bristol) and Michel Helfgott (East Tennessee State University), "A Modern Vision of the Work of Cardano and Ferrari on Quartics - Decimal Numbers Come to the Rescue," Convergence (February 2010), DOI:10.4169/loci003312




