- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
An Analysis of the First Proofs of the Heine-Borel Theorem - Cousin's Proof
Cousin's Proof
In his 1895 “Sur les fonctions de n variables complexes,” Pierre Cousin [7] extended the Heine-Borel Theorem to arbitrary covers. On page 22, he wrote:
Define a connected space S bounded by a simple or complex closed contour; if to each point of S there corresponds a circle of finite radius, then the region can be divided into a finite number of subregions such that each subregion is interior to a circle of the given set having its center in the subregion.
Before we examine the proof, we mention a few points:
- According to Dugac, this memoir was completed on October 28, 1893 (two years before Borel), but was not published until 1895 [8, p. 97]. It is very unlikely that Cousin was aware of Borel’s statement and he certainly did not make any reference to it. It appears that Cousin has at least some claim of priority for the theorem.
- Cousin’s statement is a higher-dimensional version of the Heine-Borel Theorem. Circles of finite radius would be equivalent to open intervals in one dimension.
- As Cousin did not work with the real number line in his proof, the form of completeness he used is not precisely one of those listed in our Introduction. However, there are higher-dimensional analogues of these characterizations. Specifically, Cousin made use of the following higher-dimensional version of the nested interval property:
Every nested sequence of closed, bounded sets in \({\mathbb R}^2\) has a non-empty intersection.
- It would be more accurate to refer to his “circles” as “disks” because they do not consist just of the boundary.
- No mention of countability of the cover is made, nor is it required, for this proof.
Cousin started immediately with a description of his proof technique, just as we teach our students to do, and proceeded by contradiction. He used the “divide and conquer” technique that probably appears elsewhere in a real analysis course.
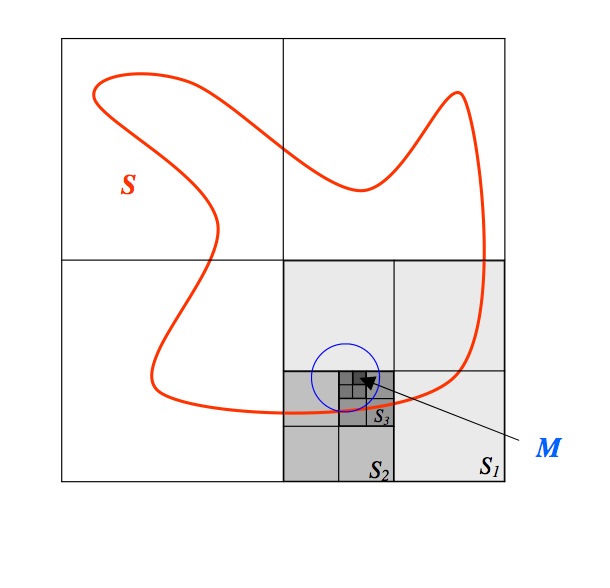
Diagram 2: In this diagram we see the “divide and conquer” method that Cousin employed in his proof.
Cousin took the region S and divided it into \(n>1\) subregions (\(n\) an integer). If the entire region required an infinite number of circles to cover it, then at least one of the subregions must also require an infinite number of circles to cover it. Cousin called that subregion S1. It is the light grey, lower right quadrant of Diagram 2.
We suppose, in fact, the lemma is false: we divide S into squares using parallels to the coordinate axes, in a way that the number of obtained regions is at least equal to a certain integer n; there is at least one of these regions S1, for which the lemma is still false.
Cousin then iterated the process, dividing S1 into n sub-subregions. At least one of these sub-subregions must require an infinite number of circles to cover it. He called this region S2 (the slightly darker grey, lower left quadrant of S1 in Diagram 2.) By continuing in this fashion, he created an infinite sequence of nested closed square regions S1 , S2 , … , Sp , … (the successively darker grey regions in Diagram 2.) He then applied the nested interval property to show there is a point M that is common to each of these Sp, and that M is in the interior or boundary of S.
Subdividing S1 into squares and portions of squares in number at least equal to n, I deduce S2, in the same way that S1 is deduced from S; in following the reasoning, I arrive at an indefinite series of squares or portions of squares S1 , S2 , … , Sp , … ; it is clear that Sp, for p increasing indefinitely, has for a limit a point M interior to S or on its perimeter; ...
Because M is in each Sp, and each Sp cannot be covered by a finite number of circles, certainly each Sp cannot be covered by a single circle. However, as Cousin noted, this is impossible, because M is in S and so some circle of positive radius covers it (the blue circle in Diagram 2). That circle will contain some Sn and all subsequent Sn+k, which is a contradiction to the way that the Sp were constructed.
... one arrives at this conclusion that one can find a square Sp surrounding M or adjacent to M which is not contained in the interior of one of the circles of the statement; however this is impossible because to the point M corresponds a circle of finite radius having this point for a center.
The following may be helpful when considering using Cousin’s proof in a class.
Background:
- A discussion of completeness in the form of the nested interval property applied to nested, closed, bounded, connected two-dimensional regions will be required.
Benefits:
- This proof has the benefit of using the “divide and conquer” technique with which students may be familiar, particularly from Bolzano-Weierstrass or one of the corollaries that we discussed above. If they have not already seen this technique, it is more likely it will appear in their studies than the “numbers of the second type” technique employed by Borel.
- Glancing through introductory analysis, topology, and set theory textbooks shows it is common to see a proof of the Heine-Borel Theorem using a technique similar to the one utilized by Cousin. Presenting Cousin’s proof as the germ of the texbook technique may be helpful for students. Recall that Borel also published a proof using this “divide and conquer” technique in [3]. While appearing years after Cousin’s paper, interested instructors may consider examining Borel’s presentation as well.
- This proof does not require the covering to be countable.
- Even if the course requires only the one-dimensional theorem, it makes for a nice student project to study a higher-dimensional analogue.
- Cousin provided a well-written proof that is easy to follow. His strategy is clearly presented at the beginning and the contradiction is noted at the end.
Drawback:
- Although Cousin’s statement is equivalent to the Heine-Borel Theorem, it certainly is not in the form that students will be using in a basic analysis course. The theorem will need to be translated into the one-dimensional case for most of the applications.
Impressions:
We believe that this proof would be particularly applicable if the Heine-Borel Theorem is being taught in a point-set topology course or in an advanced calculus class where domains of functions are often two-dimensional or higher.
Nicole R. Andre (Wittenberg University), Susannah M. Engdahl (Wittenberg University), and Adam E. Parker (Wittenberg University), "An Analysis of the First Proofs of the Heine-Borel Theorem - Cousin's Proof," Convergence (August 2013), DOI:10.4169/loci003890




