- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
An Analysis of the First Proofs of the Heine-Borel Theorem - History
History
As evidenced by the title of Dugac’s canonical paper on the chronology of the Heine-Borel Theorem, “Sur la correspondance de Borel et le théorème de Dirichlet-Heine-Weierstrass-Borel-Schoenflies-Lebesgue,” the list of names associated with the theorem is much longer than just Eduard Heine and Émile Borel. Unfortunately, this paper has not been translated from the French, and so we will review some of its details. Roughly speaking, the contributors can be broken into those who used the theorem (Dirichlet-Heine-Weierstrass) and those who proved the theorem (Borel-Schoenflies-Lebesgue). As we will see, even expanding our scope to consider these six mathematicians will be insufficient.
Certainly the first person to state (and prove) the theorem was Émile Borel (see Passage 1). In the paper “Sur quelques points de la théorie des fonctions” (1895), Borel studied the analytic continuation of functions and came across a “theorem interesting in itself” [10]. Borel deserves extensive credit for stating the result, and his proof is interesting in that it makes use of the transfinite numbers of Georg Cantor (1845-1918). However, the drawback is that he established the theorem only for a countable covering. We will examine his argument carefully in Section 3.
In 1895, the same year that Borel stated and proved his theorem, Pierre Cousin published “Sur les fonctions de n variables complexes” [7]. While stated in a slightly different way from what we see today, elements of the Heine-Borel Theorem were clearly present. In fact, M. R. Sundström stated in [18, p. 7] that, “While Heine is credited with a theorem he did not prove, it appears that Cousin was largely overlooked for a theorem he did prove.”

10. Lemma. Define a connected space S bounded by a simple or complex closed contour; if to each point of S there corresponds a circle of finite radius, then the region can be divided into a finite number of subregions such that each subregion is interior to a circle of the given set having its center in the subregion.
Passage 2: Cousin’s version of the Heine-Borel Theorem, along with a translation.
This can be considered a generalization of Borel’s Theorem in two ways. First, Cousin presented the two-dimensional case of the theorem. Also, his proof works for arbitrary coverings. We will translate and analyze his proof in Section 4.
In 1900, Arthur Schoenflies (1853-1928) wrote a report on the development of point-set topology for the German Mathematical Association [15]. He drew attention to Borel’s Theorem, which he said “extends a known theorem of Heine.” This was the first time someone attached Heine’s name to this theorem. It is questionable how similar the “known theorem” actually is to the Heine-Borel Theorem and we will see that this became a source of much contention.

To give a last example, I prove the following theorem of Borel’s, which extends a known theorem of Heine:
V. If on a straight line there is an infinite sequence of intervals \(\delta,\) so that every point of the interval \(a\) ... \(b\) is an interior point of at least one interval \(\delta,\) then there is also always a finite subset of such intervals.
Passage 3: Schoenflies’ version of the Heine-Borel Theorem, along with a translation.
We will examine Schoenflies’ argument in Section 5.
The proof Schoenflies gave followed Borel’s closely, though importantly it did work for arbitrary covers. Hildebrandt wrote, “As a matter of fact, the statement of the Borel Theorem given by Schoenflies in his 1900 Bericht can easily be interpreted to be that of the extension in question” [11, p. 425]. Henri Lebesgue (1875-1941) seemed to agree with Hildebrandt and later advocated to name the theorem Borel-Schoenflies [6, p. 68].
Others disagreed. For example, Paul Montel (1876-1975) wrote, “The name Borel-Schoenflies does not seem to me as justified as that of Heine-Borel: it seems to me that one must distinguish the theorem itself from the applications one might make with it” [8, pp. 105-106]. Borel, for his part, stated in 1903 that, “M. Lebesgue remarked that the hypothesis that the given group is countably infinite is not necessary.” Lebesgue probably said this while teaching a class at Le Collège de France in 1902-1903 [8, p. 99].
In 1902, W. H. Young (1863-1942) published another proof of the uncountable version of the Heine-Borel Theorem [19].

Passage 4: Young’s version of the Heine-Borel Theorem in an article titled “Overlapping intervals.”
Young’s proof depended on a lemma concerning “overlapping intervals.” Once that lemma was proved, the uncountable version of the Heine-Borel Theorem followed immediately. Since this paper is in English and is freely available online, we provide only an analysis in Section 6.
In 1904, Lebesgue gave a wonderfully elegant proof of the theorem in a treatise on integration [14]. Lebesgue had studied Borel’s paper in 1898, but did not notice that the cover needed to be countable. In fact, Lebesgue used the unproved uncountable version in his 1901 thesis. He took the opportunity in 1904 to prove the uncountable version.
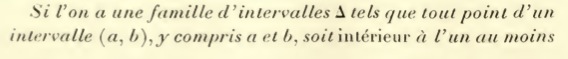

If one has a family of intervals \(\Delta\) such that any point of an interval \(\left(a,b\right),\) including \(a\) and \(b,\) is interior to at least one of \(\Delta,\) there exists a family formed of a finite number of intervals \(\Delta\) and that has the same property [any point of \(\left(a,b\right)\) is interior to one of them].
Passage 5: Lebesgue’s published version of the Heine-Borel Theorem, along with a translation.
A translation of Lebesgue’s modern and simple proof will be found in Section 7. It is this proof that most readers are likely familiar with.
A few years later, Lebesgue reviewed the text The Theory of Sets of Points by W. H. Young (who published the proof of the theorem in Passage 4, above, in 1902) and Grace Chisholm Young [13]. At the end of the review, he turned his attention to “the proposition that the authors, following the example of Messrs. Schoenfliess, Veblen, etc., call the Heine-Borel theorem.” He first explained that he had mistakenly used the uncountable version in 1901.
This demonstration had been obtained in 1898 by M. Vieillefond or by myself, I don’t know anymore, while we were studying together M. Borel’s thesis. I must confess moreover that, although I cited several times M. Borel’s statement, my attention was not held by the word countable that it contains and this is why, in my Thesis, of which the results were published in 1901, I used, without stating it, the modified theorem.
Passage 6a: Lebesgue “confessed” that he missed the word “countable” in Monsieur Borel’s statement.
He then proceeded to attack the attachment of Heine’s name to the theorem. While not the only person to question this association, Lebesgue was probably the most vocal. We’ll review some of the arguments here:
According to Hildebrandt, Schoenflies “noted the relationship of the Borel Theorem to Heine’s proof of the uniform continuity of a function continuous on a closed interval, published in 1872” [11, p. 424]. The name Heine-Borel grew in popularity after it appeared in Young’s proof (Passage 4, above). Lebesgue (Passage 5) did not use Heine’s name. Schoenflies defended his choice in the January 24, 1907 issue of Comptes Rendus, stating that Heine’s uniform continuity theorem is the geometric analogue to Borel’s Theorem [16, p. 22]. Schoenflies sent a copy of this note to Lebesgue prior to publication. Lebesgue wrote back immediately calling the association “ridiculous,” and restated his position in the same journal a few months later [8, p. 105].
Schoenflies’ association of Heine with the theorem was tenuous partly because the connection between Heine and the uniform continuity theorem is itself questionable! Whereas Heine first published the uniform continuity theorem (which does contain a germ of the Heine-Borel Theorem), it was Heine’s professor, Dirichlet, who first realized the uniform continuity theorem and presented the proof in a class he was teaching in 1852. Although Dirichlet’s notes were not published until 1904, Heine wrote a paper in 1872 that gave several results that can be found in those lectures, including the uniform continuity theorem. According to Bressoud, he used “precisely Dirichlet’s argument. Heine did not credit Dirichlet” [6, p. 68].
Lebesgue noted there were many mathematicians in addition to Heine who implicitly used Borel’s Theorem [13, p. 134].
It is therefore not surprising that during arguments made in order to prove such uniformities one incidentally finds demonstrated M. Borel’s theorem; one can cite the reasoning of Heine (Journ. de Crelle, 1872), of M. Goursat (Trans. of the Am. Math. Soc.), of M. Baire (Ann. di Mat., 1900). It is moreover strongly possible that in searching a little, in glancing through, for example, the works of Cauchy, of Seidel, of Stokes, one finds some arguments to cite previous to those of Heine.
Passage 6b: Lebesgue questioned attaching Heine’s name to the theorem.
To the mathematicians Heine, Edouard Goursat (1858-1936), René Baire (1874-1932), Augustin-Louis Cauchy (1789-1857), Philipp von Seidel (1821-96), and George Stokes (1819-1903), we could add the names of Lejeune Dirichlet (1805-59), Karl Weierstrass (1815-97), and Salvatore Pincherle (1853-1936) [6] and probably many others.
Lebesgue disliked crediting people who incidentally used the theorem, noting that the merit was in Borel’s “perceiving it, stating it, and guessing its interest.” He instead offered Borel-Schoenflies. Others campaigned for Borel-Lebesgue, which is still a common name for the theorem. As noted above, Borel himself preferred “the first fundamental theorem of measure theory” [6, pp. 68-69]. It is interesting that Schoenflies eventually caved and dropped Heine’s name from the 1913 edition of his 1900 book [11, p. 424].
Finally, the reader may notice that the word “compact” never appears in these theorems, though it is often found in modern statements of the Heine-Borel Theorem. Fréchet introduced this terminology in 1906 [18, p. 10], and so none of these proofs, published from 1895 to 1904, contained that language.
Let us now turn our attention to the proofs.
Nicole R. Andre (Wittenberg University), Susannah M. Engdahl (Wittenberg University), and Adam E. Parker (Wittenberg University), "An Analysis of the First Proofs of the Heine-Borel Theorem - History," Convergence (August 2013), DOI:10.4169/loci003890




