- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Cubes, Conic Sections, and Crockett Johnson - Note from Johnson to Mickey Rosenau

Figure 10. Note from Crockett Johnson (David Johnson Leisk) to Mickey Rosenau. (Courtesy of the Smithsonian Institution, image number AHB2013q009103.)
The note in Figure 10 was written after Johnson created the painting, The Problem of Delos (Menaechmus), shown in Figure 8 on the preceding page. It was probably written in 1970, as the “Cambridge math mag [the Mathematical Gazette] that published [his] squared circle” did so that year. The “math mag” did not publish the item he referred to in the note, but around that time Johnson began working on an article he called “Geometric Geometric Paintings” [Note 1] that was to consist of discussions of twelve of his paintings. In 1972 Johnson published a shorter version of this article, “On the Mathematics of Geometry in My Abstract Paintings,” in the journal Leonardo. The first diagram mentioned in the note of Figure 10 and shown in Figure 11 is not related to cube roots but is one on which he based his painting, Division of a One-by-Two Rectangle by Conic Rectangles, one of the seven paintings discussed in the Leonardo article.
The second diagram, however, is related to cube roots since Johnson noted that “\(AJ/AB = 1.25992\dots = \sqrt[{\bf 3}]{2}.\)” Furthermore, it appears in early drafts of the section, “FACE OF CUBE AND A SQUARE EQUALLING ITS VOLUME (Artist’s Construction)” [Note 2]. Although we cannot be sure, it seems likely that Johnson used an approximation of his listed value of AB, \(1.28423\dots,\) to place point B since he used approximations to place similar points in other constructions found in drafts of “Geometric Geometric Paintings.” In other words, without the aid of a mark on the straightedge, the compass and straightedge of the classic Greek constructions cannot determine the cube root of two and, therefore, can only stand watching as the two parabolas and hyperbola easily double the cube.
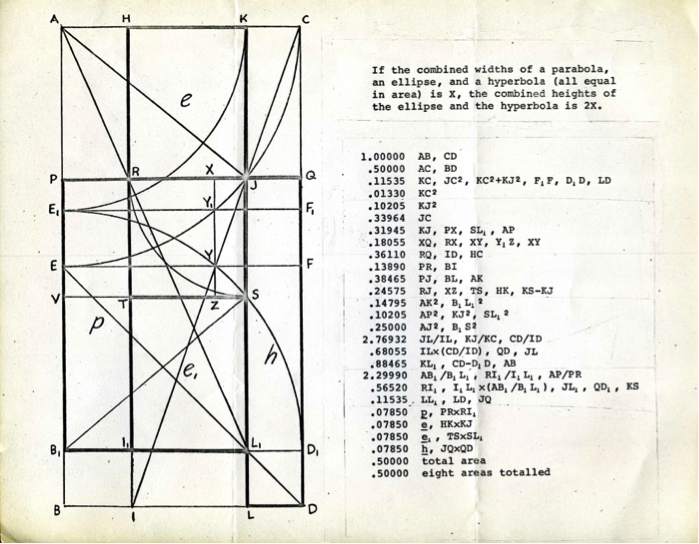
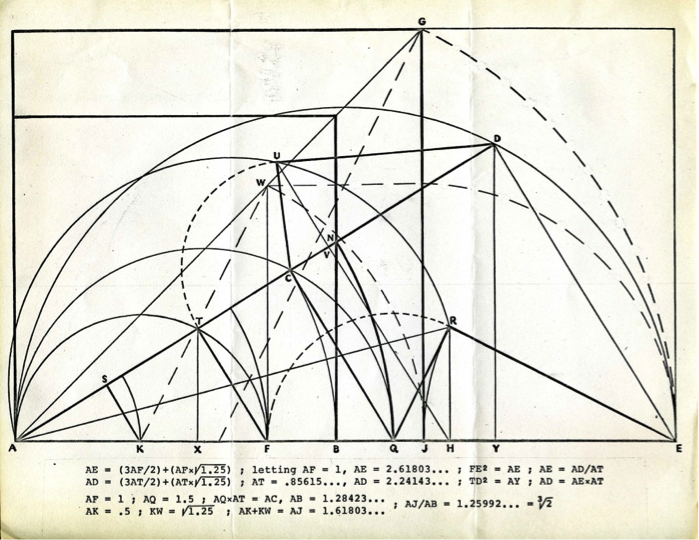
Figure 11. The two diagrams accompanying Johnson's note to Rosenau in Figure 10. (Courtesy of the Smithsonian Institution, image numbers AHB2013q009104 and AHB2013q009105.)
Notes:
1) In her 2013 article on his paintings, Peggy Kidwell made the point that his explanation of this title, specifically its redundancy, “well express[es] the distinction between his use of mathematics and that of contemporary painters” [p. 207].
2) No painting with this name appears on either a 1980 list of Johnson’s paintings or the list on the Crockett Johnson Homepage. A painting with a similar name, Cube and Square of Equal Value (Artist's construction), appears on the 1980 list, although without a photograph.
Stephanie Cawthorne (Trevecca Nazarene University) and Judy Green (Marymount University), "Cubes, Conic Sections, and Crockett Johnson - Note from Johnson to Mickey Rosenau," Convergence (March 2014)




