- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Extending al-Karaji's Work on Sums of Odd Powers of Integers - The Sums of the Seventh and Ninth Powers
Vidinli now applies the same procedure to the differences of fourth powers of \(S_n\) .
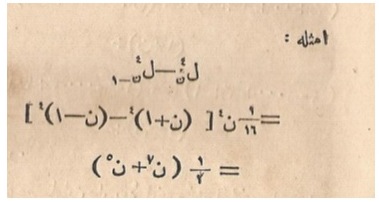
Figure 8. Difference of fourth powers (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
Figure 8 shows only: \[ S_n^{\,4} - S_{n-1}^{\,\,4} = {\frac{1}{16}}n^4 \Big({(n+1)}^4 - {(n-1)}^4 \Big) = {\frac{1}{2}}(n^7 + n^5) .\]
Providing a few more details for this calculation, we have the following differences: \begin{align} S_n^{\,4} - S_{n-1}^{\,\,4} &= {\bigg[ {\frac{n(n+1)}{2}}\bigg]}^4 - {\bigg[ {\frac{(n-1)n}{2}}\bigg]}^4 \\ &= {\frac{n^4}{16}} \Big({(n+1)}^4 - {(n-1)}^4 \Big) \\ &= {\frac{n^4}{16}}(n^4 + 4n^3 + 6n^2 + 4n +1 - n^4 + 4n^3 - 6n^2 + 4n - 1) \\ &= {\frac{n^4}{16}}(8n^3 + 8n) \\ &= {\frac{1}{2}}(n^7 + n^5) , \\ S_{n-1}^{\,\,4} - S_{n-2}^{\,\,4} & = {\frac{1}{2}}\big((n-1)^7 + (n-1)^5\big) , \\ \\ \\ \dots\dots\dots & \dots\dots\dots\dots\dots ,\\ \\ S_2^{\,4} - S_{1}^{\,4} & = {\frac{1}{2}}(2^7 + 2^5) , \\ S_1^{\,4} - S_{0}^{\,4} & = {\frac{1}{2}}(1^7 + 1^5) .\end{align}
If we add these equations, we get: \[ {S_n^{\,4}} = {\frac{1}{2}}\Big(1^7 + 2^7 + 3^7 + \cdots + n^7\Big) + {\frac{1}{2}}\Big(1^5 + 2^5 + 3^5 + \cdots + n^5\Big) ,\] or \begin{align} {{(1+2+3+\cdots +n)}^4} & = {\frac{1}{2}}\Big({1^5 + 2^5 + 3^5 + \cdots + n^5}\Big) \\ & + {\frac{1}{2}}\Big({1^7 + 2^7 + 3^7 + \cdots + n^7}\Big) ,\end{align} as can be seen in Figure 9.
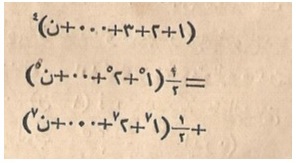
Figure 9. An equation involving the sum of the seventh powers (from Mebahis-i İlmiyye, 1867, courtesy of the authors).
We already know that \[ {1^5 + 2^5 + 3^5 + \cdots + n^5} = {\frac{4}{3}}\Bigg({{\bigg[ {\frac{n(n+1)}{2}}\bigg]}^3 - {\frac{1}{4}}{\bigg[ {\frac{n(n+1)}{2}}\bigg]}^2}\Bigg) \] and \[{1 + 2 + 3 + \cdots + n} = {\frac{n(n+1)}{2}}.\] When we substitute these identities into the equation in (or just above) Figure 9, we can find a formula for the sum of the seventh powers: \[ {1^7 + 2^7 + 3^7 + \cdots + n^7} = {\frac{1}{8}}n^8 + {\frac{1}{2}}n^7 + {\frac{7}{12}}n^6 - {\frac{7}{24}}n^4 + {\frac{1}{12}}n^2 . \] Readers can complete the calculuation (see Exercise 2), and can check the result by substituting an "\( n\)" of their choice.
Vidinli did not continue after the differences of fourth powers and the sum of the seventh powers. Just out of curiosity, we computed differences of fifth powers, with the following result. \begin{align} S_n^{\,5} - S_{n-1}^{\,\,5} &= {\bigg[ {\frac{n(n+1)}{2}}\bigg]}^5 - {\bigg[ {\frac{(n-1)n}{2}}\bigg]}^5 \\ &= {\frac{n^5}{32}} \Big({(n+1)}^5 - {(n-1)}^5 \Big) \\ &= {\frac{n^5}{32}}(10n^4 +20n^2 + 2) \\ &= {\frac{5}{16}}n^9 +{\frac{5}{8}}n^7 + {\frac{1}{16}}n^5 .\end{align} If we continue the process, we can find a formula for the sum of the ninth powers. Try it! (See Exercise 3.)
Hakan Kursat Oral (Yildiz Technical University) and Hasan Unal (Yildiz Technical University), "Extending al-Karaji's Work on Sums of Odd Powers of Integers - The Sums of the Seventh and Ninth Powers," Convergence (August 2011), DOI:10.4169/loci003725




