- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Appendix B: Solutions
Below, we have provided at least one solution to each of the 11 problems selected from the Pamiers text. Other methods of solution may be possible.
Problem 1. Two merchants want to barter together, planning to exchange their merchandise; and the first of them has wool and the other has cloth. The one who has cloth wants 24 sous for trading each bolt of cloth whose cash price is but 20 sous. I ask for how much the other must sell each quintal of wool that is worth but 12 liras, in order that he lose nothing.
The author of the Pamiers manuscript showed solutions similar to B and C below.
Solution A: a proportion using the augmented (“marked-up”) selling prices
Begin with the proportion,
20 sous : 24 sous :: 12 liras : ?
(This is like asking, “A marked-up price of 24 sous on a list price of 20 sous is equivalent to a marked-up price of how many liras on a list price of 12 liras?)
By the rule of three, the marked-up price is therefore (12 × 24) ÷ 20 = 288 ÷ 20 = 14 2/5 liras, or 14 liras 8 sous.
Solution B: a proportion using the markups
Begin with the proportion,
20 sous : 4 sous :: 12 liras : ?
(This is like asking, “A markup of 4 sous on a list price of 20 sous is equivalent to a markup of how many liras on a list price of 12 liras?)
By the rule of three, the markup is therefore (12 × 4) ÷ 20 = 48 ÷ 20 = 2 2/5 liras, or 2 liras 8 sous.
Augmenting the price of 12 liras by the markup of 2 liras 8 sous gives a marked-up price of 14 liras 8 sous.
Solution C: double false position using the markups
Begin with the proportion,
20 sous : 4 sous :: 12 liras : ?
Note 12 × 4 = 48.
First, suppose the markup is 2 liras. But 20 × 2 = 40, a deficit of 8.
Second, suppose the markup is 3 liras. But 20 × 3 = 60, an excess of 12.
By double false position, the correct markup is therefore
\[{\frac{(2\times12\,{\rm excess})+(3\times8\,{\rm deficit})}{12\,{\rm excess}\,+8\,{\rm deficit}}}={\frac{48}{20}}\]\[=2\frac{2}{5}\,{liras}=2\,{liras}\,\,8\,{sous}.\]
Augmenting the price of 12 liras by the markup of 2 liras 8 sous gives a marked-up price of 14 liras 8 sous.
Problem 2. If 3 deniers of Perpignan are worth 5 deniers of Montpellier, and 2 of Montpellier are worth 3 of those of Avignon, I ask how many of those of Perpignan are worth 12 of those of Avignon.
The author showed a solution similar to A below.
Solution A: composite rule of three \[\frac{5}{3}\times\frac{3}{2}=\frac{5}{2}\]
5 : 2 :: 12 : ?
(12 × 2) ÷ 5 = 24 ÷ 5 = 4 4/5 deniers.
Solution B: chain rule
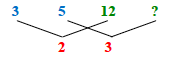
(3 × 2 × 12) ÷ (5 × 3) = 24 ÷ 5 = 4 4/5 deniers.
Solution C: algebra
Given \(3P=5M,\) and \(2M=3A,\) we have \[P={\frac{5}{3}}M,\quad M={\frac{3}{2}}A\] \[P={\frac{5}{3}}\left({\frac{3}{2}}{A}\right) = {\frac{5}{2}}A\] \[{\frac{2}{5}}P=A\] \[12\left({\frac{2}{5}}P\right)=12A\] \[{\frac{24}{5}}P=12A\]
Thus, 24/5 or 4 4/5 deniers of Perpignan are worth 12 of those of Avignon.
Problem 3. A merchant paid 10 liras, which is 200 sous, for two manners of grain, namely wheat and oats, and he purchased each setier of wheat for 10 sous and each setier of oats for 5 sous. This merchant turned around and sold his grain, selling each setier of oats for 4 sous and each setier of wheat for 12 sous, and realized a profit of 10 sous. I ask how many setiers of wheat and how many of oats he purchased, and how much money he paid for each grain.
The author showed a solution similar to A below.
Solution A: double false position
First, suppose he sold 10 setiers of wheat at 10 sous, thus 100 sous total.
Then he paid 200 – 100 = 100 sous for the oats at 5 sous,
and thus purchased 100 ÷ 5 = 20 setiers of oats.
So his sales proceeds are
(10 setiers of wheat at 12 sous) + (20 setiers of oats at 4 sous) = 120 + 80 = 200 sous
and his profits are therefore
200 – 200 = no sous, instead of the stated 10 sous (thus, deficit 10).
Likewise, suppose he sold 15 setiers of wheat. Then we get
200 – 150 = 50
50 ÷ 5 = 10
(15 × 12) + (10 × 4) = 220
and his profits are therefore
220 – 200 = 20 sous, instead of the stated 10 sous (thus, excess 10).
By double false position, the correct amount is thus \[{\frac{(10\,{setiers}\,\times10\,{sous}\,{\rm excess})+{(15\,{setiers}\,\times10\,{sous}\,{\rm deficit})}}{10\,{sous}\,{\rm excess}+10\,{sous}\,{\rm deficit}}}=\frac{250}{20}=12\frac{1}{2}\] setiers of wheat. Therefore, he paid 12 1/2 × 10 = 125 sous for the wheat and 200 – 125 = 75 sous for the oats, and so the quantity of oats purchased was 75 ÷ 5 = 15 setiers.
Check. The proceeds were thus (12 1/2 × 12) + (15 × 4) = 210 sous, a profit of 210 – 200 = 10 sous.
Solution B: algebra (simple elimination)
Let \(x=\) the quantity of wheat, and \(y=\) the quantity of oats. Then \[10x+5y=200\] \[12x+4y=210.\]
Dividing the equations by \(5\) and \(4,\) respectively, we get \[2x+y=40\] \[3x+y=52.5.\]
Subtracting the first equation from the second eliminates the second variable, leaving \[x=12.5,\]
so \(12.5\) setiers of wheat were purchased for \(12.5\times 10=125\) sous.
Back-substituting this result yields \[2(12.5)+y=40\] \[25+y=40\] \[y=15,\]
so \(15\) setiers of oats were purchased for \(15\times 5=75\) sous.
Solution C: matrix algebra
Given \[\left[ {\begin{array}{cc}
10&5 \\
12&4 \\ \end{array}}\right]\left[ {\begin{array}{c}
x\\
y\\ \end{array}}\right]=\left[ {\begin{array}{c}
200\\
210\\ \end{array}}\right],\]
the quantities of wheat and oats purchased were \[\left[ {\begin{array}{c}
x\\
y\\ \end{array}}\right]={{\left[ {\begin{array}{cc}
10&5 \\
12&4 \\ \end{array}}\right]}^{-1}}\left[ {\begin{array}{c}
200\\
210\\ \end{array}}\right]=\left[ {\begin{array}{c}
12.5\\
15\\ \end{array}}\right];\]
that is, 12.5 setiers of wheat and 15 setiers of grain, and so the amounts paid were 10 × 12.5 = 125 sous and 5 × 15 = 75 sous, respectively.
Problem 4. A merchant purchased three pieces of cloth that cost him [a total of] 30 motos, and doesn’t know with certainty what each of the pieces cost, but does know that the second cost double the first and 4 more; the third cost three times as much as the second, less 7. I ask what each one cost.
The author showed a solution similar to A below.
Solution A: double false position
Suppose the first piece cost 3 motos.
Then the second piece cost (2 × 3) + 4 = 10 motos,
and the third piece cost (3 × 10) – 7 = 23 motos.
But 3 + 10 + 23 = 36 motos, an excess of 6.
Suppose the first piece cost 4 motos.
Then the second piece cost (2 × 4) + 4 = 12 motos,
and the third piece cost (3 × 12) – 7 = 29 motos.
But 4 + 12 + 29 = 45 motos, an excess of 15.
By double false position, the true position is thus \[{\frac{(3\times15\,{\rm excess})-{(4\times\,6\,{\rm excess})}}{15\,{\rm excess}-6\,{\rm excess}}}=\frac{21}{9}.\]
Therefore, the first piece cost \(\frac{21}{9}\) or \(2\frac{1}{3}\) motos,
the second piece cost \(\left(2\times2\frac{1}{3}\right)+4=8\frac{2}{3}\) motos,
and the third piece cost \(\left(3\times8\frac{2}{3}\right)-7=19\) motos.
Check. The total cost was thus \(2\frac{1}{3}+8\frac{2}{3}+19=30\) motos.
Solution B: algebra
Let x = the cost of the first piece.
Then the cost of the second piece is 2x + 4,
and the cost of the third piece is 3(2x + 4) – 7.
Since the total cost of the three pieces is 30 motos, we have:
x + (2x + 4) + (3(2x + 4) – 7) = 30.
x + (2x + 4) + (6x + 12 – 7) = 30.
9x + 9 = 30
9x = 21
x = \(\frac{21}{9}\) or \(2\frac{1}{3}\) motos, etc. as in Solution A above.
Problem 5. Three merchants formed a company together. The first advanced 200 motos and stayed for 15 months, the second advanced 94 motos and stayed for 17 months, the third advanced 38 motos and stayed for 10 months; and at the end they realized a profit of 400 [motos]. I ask how it should be divided [among them].
Solution by proportion:
200 motos × 15 months = 3000
94 motos × 17 months = 1598
38 motos × 10 months = 380
Total = 4978.
The lattice or gelosia technique proceeds as follows for the second of the three multiplications noted above.
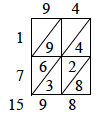
Using the rule of three, the proportional shares of the profit are, respectively,
4978 : 3000 :: 400 : ? implies 400 × 3000 ÷ 4978 = \(241\frac{151}{2489}\) motos
4978 : 1598 :: 400 : ? implies 400 × 1598 ÷ 4978 = \(128\frac{1008}{2489}\) motos
4978 : 380 :: 400 : ? implies 400 × 380 ÷ 4978 = \(30\frac{70}{131}\) motos.
Check. The total profit is thus \(241\frac{151}{2489}+128\frac{1008}{2489}+30\frac{70}{131}=400\) motos.
Problem 6. A merchant gave 600 liras to a factor who had 200 liras of his own, by such arrangement that he work with that 800 liras for 5 years, and at the end of that time [said the merchant] we will divide in half the principal and the profit. It so happened that the factor spent none of the 200 liras, but had made use of the 600 liras of the merchant; and at the end of 5 years had realized 2400 liras, counting principal and profit. I ask how the division should be carried out— considering that the factor spent none of what he should have spent— in order that the merchant not be deceived.
Solution by proportion:
By agreeing in advance to divide their proceeds in half, the two men were valuing equally their prospective contributions: 600 liras from the merchant, and 200 liras plus 5 years of labor from the factor. Therefore, the value of the factor’s five years of labor was 600 – 200 = 400 liras.
The factor’s 200 liras of money that ended up not being needed for production cannot be thought of as part of the investment, since throughout the five years the factor was free to use that money in any way that pleased him. Therefore, the total value invested by the two men together was 600 + 400 = 1000 liras, and the total proceeds on the investment itself were 2400 – 200 = 2200 liras. These 2200 liras must be divided between the two men in proportion to their respective shares in the investment, namely 600 and 400 liras. Using the rule of three,
merchant’s share, 1000 : 600 :: 2200 : ? implies 2200 × 600 ÷ 1000 = 1320 liras
factor’s share, 1000 : 400 :: 2200 : ? implies 2200 × 400 ÷ 1000 = 880 liras.
(The factor also retains his unused 200 liras for a total of 1080 liras.)
Check. The total proceeds were thus 1320 + 880 = 2200 liras.
Problem 7. Two merchants went to the fair; the first had 20 sacks of wool, for which he paid the duty collector 1 sack of the wool, and the collector returned to him 2 liras; the second had 60 sacks of wool, for which he paid the collector 2 sacks of wool plus 6 liras. I ask the value of each sack of the wool, and how much was paid the collector per sack.
The author showed a solution similar to A below.
Solution A: double false position
First, suppose the value of each sack is 4 liras.
Then the tax on 20 sacks, being 1 sack minus 2 liras, is 4 – 2 = 2 liras.
Thus, the tax on 60 sacks is 3 × 2 = 6 liras,
instead of the stated 2 sacks plus 6 liras, or (2 × 4) + 6 = 14 liras.
Therefore, the deficit is 14 – 6 = 8 liras.
Second, suppose the value of each sack is 8 liras.
Then the tax on 20 sacks, being 1 sack minus 2 liras, is 8 – 2 = 6 liras.
Thus, the tax on 60 sacks is 3 × 6 = 18 liras,
instead of the stated 2 sacks plus 6 liras, or (2 × 8) + 6 = 22 liras.
Therefore, the deficit is 22 – 18 = 4 liras.
By double false position, the correct value of each sack is therefore \[{\frac{(8\times8\,{\rm deficit})-{(4\times4\,{\rm deficit})}}{8\,{\rm deficit}-4\,{\rm deficit}}}=\frac{48}{4}=12\,\,{liras}.\]
To find the tax rate, recall that the tax on 20 sacks was 1 sack minus 2 liras, or 12 – 2 = 10 liras. Thus, the tax rate was 10 liras ÷ 20 sacks = ½ lira per sack.
Check. The tax on 60 sacks was 2 sacks plus 6 liras = (2 × 12) + 6 = 30 liras, for a rate of 30 liras ÷ 60 sacks = ½ lira per sack.
Solution B: algebraic style, by student Alex Wolstencroft (Schoolcraft College)
We are given:
tax on 20 sacks = 1 sack – 2 liras
tax on 60 sacks = 2 sacks + 6 liras.
Multiplying the first equation by 3, we get
tax on 60 sacks = 3 sacks – 6 liras.
Comparing with the second equation,
2 sacks + 6 liras = 3 sacks – 6 liras
2 sacks = 3 sacks – 12 liras
1 sack = 12 liras.
Putting this in the first equation,
tax on 20 sacks = 12 liras – 2 liras
tax on 20 sacks = 10 liras
tax on 1 sack = 10/20 lira = ½ lira.
Solution C: symbolic algebra
Let x = the value of each sack, in liras, and y = the tax on each sack, in liras.
Then we are given:
20y = x – 2
60y = 2x + 6
Multiplying the first equation by 3, we get
60y = 3x – 6.
Comparing with the second equation,
3x – 6 = 2x + 6
x = 12 liras per sack
y = (x – 2)/20 = 10/20 = ½ lira per sack.
Problem 8. A man entered a fair, and the first day doubled all his money and spent 1 gros; likewise on the second tripled all his money that he had left and spent 2 gros; likewise on the third quadrupled his money that he had left and spent 2 gros, and found that he had nothing but 3 gros. I ask how much money he carried [to the fair].
The author showed a solution similar to A below.
Solution A: double false position
First, suppose he entered with 1 gros.
After Day 1: (2 × 1) – 1 = 1 gros
After Day 2: (3 × 1) – 2 = 1 gros
After Day 3: (4 × 1) – 2 = 2 gros instead of the stated 3 gros (deficit 1).
Second, suppose he entered with 2 gros.
After Day 1: (2 × 2) – 1 = 3 gros
After Day 2: (3 × 3) – 2 = 7 gros
After Day 3: (4 × 7) – 2 = 26 gros instead of the stated 3 gros (excess 23).
Therefore, by double false position, the correct amount with which he entered the fair is\[{\frac{(1\times23\,{\rm excess})+{(2\times1\,{\rm deficit})}}{23\,{\rm excess}+1\,{\rm deficit}}}=\frac{25}{24}=1\frac{1}{24}\,\,{gros}.\]
Check.
After Day 1: (2 × 1 1/24) – 1 = 1 1/12 gros
After Day 2: (3 × 1 1/12) – 2 = 1 1/4 gros
After Day 3: (4 × 1 1/4) – 2 = 3 gros.
Solution B: inversion (“working backward”)
Before Day 3: (3 + 2) ÷ 4 = 5/4 gros
Before Day 2: (5/4 + 2) ÷ 3 = 13/12 gros
Before Day 1: (13/12 + 1) ÷ 2 = 25/24 or 1 1/24 gros.
Solution C: algebra
Let \(x =\) the amount with which he entered the fair, in gros.
Then we are given \(4\left[3\left(2x-1\right)-2\right]-2=3,\)
so \[12(2x-1)-8-2=3\] \[24x-12-8-2=3\] \[24x=25\] \[x=\frac{25}{24}=1\frac{1}{24}\,\,{gros}.\]
Problem 9. A vat [of wine] has three spigots, the first bigger than the others, and in such a manner that with the biggest open, all the wine empties in 3 hours; and with the medium one open, it empties in 4 hours; and with the smallest open, it empties in 6 hours. I ask when all the spigots are open together, in how much time will the wine empty.
The author showed a solution similar to A below.
Solution A: single false position
Suppose the time needed to empty 1 vat is 12 hours (chosen purely for convenience, since 12 is divisible by 3, 4, and 6).
In that time, the three spigots together would drain \[\left({\frac{1\,{\rm vat}}{3\,{\rm hrs}}}\times12\,{\rm hrs}\right)+\left({\frac{1\,{\rm vat}}{4\,{\rm hrs}}}\times12\,{\rm hrs}\right)+\left({\frac{1\,{\rm vat}}{6\,{\rm hrs}}}\times12\,{\rm hrs}\right)=9\,\,{\rm vats},\]
instead of the correct 1 vat. Thus, the supposition was too large by a factor of 9, indicating that the correct answer is 12 ÷ 9 = 1 1/3 hrs, or 80 mins.
Solution B: additive rates
Since the rates (vats/hour) are additive, the net rate of drainage is \[\frac{1}{3}+\frac{1}{4}+\frac{1}{6}=\frac{9}{12}=\frac{3}{4}\frac{\rm vats}{\rm hour}.\]
Thus, the net time is \(\frac{4}{3}\frac{\rm hours}{\rm vat}\) or \(1\frac{1}{3}\frac{\rm hours}{\rm vat}.\)
Problem 10. Two men leave on the same day and the same hour from two cities, say for example the first leaves Béziers for Barcelona and the other goes from Barcelona to Béziers. And the one that leaves Béziers does the route in 7 days, and the other takes 9 days. I ask how much time is required before they see each other, and [if the cities are separated by 63 leagues] how far each has traveled.
The author showed a solution similar to A below.
Solution A: single false position
Suppose 4 days are required before the men see each other (chosen for convenience, since 4 is half of the 8-day average of the 7 and 9 days required by each man, respectively, to traverse the entire route alone).
In that time, the two men together would cover \[\left({\frac{1\,{\rm route}}{7\,{\rm days}}}\times4\,{\rm days}\right)+\left({\frac{1\,{\rm route}}{9\,{\rm days}}}\times4\,{\rm days}\right)=\frac{4}{7}+\frac{4}{9}=\frac{64}{63}\,\, {\rm route},\]
instead of the correct 1 route. Thus, the supposition was too large by a factor of 64/63, indicating that the correct answer is 4 days ÷ (64/63) = 63/16 or 3 15/16 days.
The distance covered by each man can then be found by multiplying rate by time:
The first man covers \[{\frac{1\,{\rm route}}{7\,{\rm days}}}\times{{\frac{63}{16}}\,{\rm days}}={\frac{9}{16}\,{\rm route}}={{\frac{9}{16}}\left(63\,{\rm leagues}\right)}={35\frac{7}{16}\,{\rm leagues}}.\]
The second man covers \[{\frac{1\,{\rm route}}{9\,{\rm days}}}\times{{\frac{63}{16}}\,{\rm days}}={\frac{7}{16}\,{\rm route}}={{\frac{7}{16}}\left(63\,{\rm leagues}\right)}={27\frac{9}{16}\,{\rm leagues}}.\]
Check. The total distance covered by the two men is thus 35 7/16 + 27 9/16 = 63 leagues.
Solution B: additive rates
Since the rates (routes/day) are additive, the net rate of speed is \[\frac{1}{7}+\frac{1}{9}=\frac{16}{63}\frac{\rm routes}{\rm day}.\]
Thus, the net time is 63/16 or 3 15/16 days/route. The distance covered by each man can then be found by multiplying rate by time, as in Solution A above.
Solution C: algebra
Using subscripts \(1\) and \(2,\) respectively, to distinguish quantities for the two men, their speeds (rates) are:
\[r_1 =\frac{1\,\rm route}{7\,\rm days}=\frac{63\,\rm leagues}{7\,\rm days}=9\frac{\rm leagues}{\rm day}\]
\[r_2 =\frac{1\,\rm route}{9\,\rm days}=\frac{63\,\rm leagues}{9\,\rm days}=7\frac{\rm leagues}{\rm day}.\]
Since the distances covered by the two men must total 63 leagues, we have \(d_1+d_2=63\) leagues, and so the time \(t,\) in days, required before the men see each other satisfies: \[r_1t+r_2t=63\,\,{\rm leagues}\] \[9t+7t=63\] \[16t=63,\] so that \(t=\frac{63}{16}\) or \(3\frac{15}{16}\) days. The distance covered by each man can then be found by multiplying rate by time, as in Solution A above.
Problem 11. There are 5 men who [each] want to purchase a piece of cloth in such manner [i.e., at such a cost] that the first asks of all the others 1/2 of all the gold and silver they carry, the second asks 1/3, the third asks 1/4, the fourth [asks] 1/5 and the fifth asks 1/6. I ask what the piece cost and what each of them carried.
All solutions differ from one another by an arbitrary multiplicative constant (scaling factor). The author showed, without justification, a rote solution similar to A below. I follow that with my own justification of the rote procedure, and then a solution using matrix algebra.
Solution A: rote procedure
Start with the multiplier 60 (chosen purely for convenience, since 60 is divisible by 2, 3, 4, and 5).
Divide this multiplier by the complements of the stated fractions 1/2, 1/3, …, 1/6:
60 ÷ (1 – 1/2) = 120
60 ÷ (1 – 1/3) = 90
60 ÷ (1 – 1/4) = 80
60 ÷ (1 – 1/5) = 75
60 ÷ (1 – 1/6) = 72.
Add these quotients and divide by one less than the number of men involved:
(120 + 90 + 80 + 75 + 72) ÷ (5 – 1) = 437 ÷ 4 = 109¼,
which gives the total sum carried by the men. The money that each man carried individually is found by subtracting each of the above quotients from this number, one by one:
109¼ – 120 = -10¾
109¼ – 90 = 19¼
109¼ – 80 = 29¼
109¼ – 75 = 34¼
109¼ – 72 = 37¼.
The price of the piece of cloth can be found by subtracting the chosen multiplier from this same number:
109¼ – 60 = 49¼.
Check. We check that each man can meet the price according to his claim:
-10¾ + 1/2(120) = 49¼
19¼ + 1/3(90) = 49¼
29¼ + 1/4(80) = 49¼
34¼ + 1/5(75) = 49¼
37¼ + 1/6(72) = 49¼.
Justification for the rote procedure:
Let \(x_i =\) the money that man \(i\) carries
\({\overline{x_i}}=\) the money that the other 4 men carry
\(T=x_i +{\overline{x_i}}=\) the total money carried
\(c=\) the cost of the piece of cloth
\(x = T – c =\) the excess money.
Taking man 5 as an example, we start with the given condition: \[x_5 +\frac{1}{6}{\overline{x_5}}=c\] \[x_5 +{\overline{x_5}}=c+\frac{5}{6}{\overline{x_5}}\] \[T=c+\frac{5}{6}{\overline{x_5}}\] \[x=\frac{5}{6}{\overline{x_5}}\] \[{\frac{x}{\frac{5}{6}}}={\overline{x_5}}.\]
Similarly, \[{\frac{x}{\frac{4}{5}}}={\overline{x_4}},\,\,{\rm etc.}\] Summing all 5 such equations, we get \[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}={\overline{x_1}}+\cdots+{\overline{x_5}}.\]
Since the money that any one man carries is included in 4 of the 5 terms on the right-hand side, the total on the right is \(4T:\) \[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}=4T\] \[\frac{1}{4}\left[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}\right]=T\]
The parameter \(x\) is an arbitrary multiplicative constant, whose choice determines each \(x_i\) and thus their total, \(T.\) To determine the money that any man carries, say man 5, \[x_5=T-{\overline{x_5}}\] \[x_5={\frac{1}{4}}{\left[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}\right]}-{\frac{x}{\frac{5}{6}}},\]
and to determine the cost, \[c=T-x\] \[c=\frac{1}{4}\left[{\frac{x}{\frac{1}{2}}}+\cdots+{\frac{x}{\frac{5}{6}}}\right]-x.\]
Solution B: matrix algebra
Let \(x_i=\) the money that man \(i\) carries and \(c =\) the cost of the piece of cloth.
The given conditions can be thought of as a system of 5 linear equations and 5 unknowns, with a common parameter on the right-hand side: \[ {\begin{array}{r} x_1+\frac{1}{2}\left(x_2+x_3+x_4+x_5\right)=c\\ x_2+\frac{1}{3}\left(x_1+x_3+x_4+x_5\right)=c\\ x_3+\frac{1}{4}\left(x_1+x_2+x_4+x_5\right)=c\\ x_4+\frac{1}{5}\left(x_1+x_2+x_3+x_5\right)=c\\ x_5+\frac{1}{6}\left(x_1+x_2+x_3+x_4\right)=c\\ \end{array}}\]
In matrix form, this becomes: \[\left[ {\begin{array}{ccccc} 1&{\frac{1}{2}}&{\frac{1}{2}}&{\frac{1}{2}}&{\frac{1}{2}} \\{\frac{1}{3}}&1&{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}} \\{\frac{1}{4}}&{\frac{1}{4}}&1&{\frac{1}{4}}&{\frac{1}{4}} \\{\frac{1}{5}}&{\frac{1}{5}}&{\frac{1}{5}}&1&{\frac{1}{5}} \\{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&{\frac{1}{6}}&1 \\ \end{array}}\right] \left[ {\begin{array}{l} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ \end{array}}\right] =c \left[ {\begin{array}{c} 1\\ 1\\ 1\\ 1\\ 1\\ \end{array}}\right]\]
\[\left[ {\begin{array}{l} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ \end{array}}\right] = c{{\left[ {\begin{array}{ccccc} 1&1/2&1/2&1/2&1/2 \\ 1/3&1&1/3&1/3&1/3 \\ 1/4&1/4&1&1/4&1/4 \\ 1/5&1/5&1/5&1&1/5 \\ 1/6&1/6&1/6&1/6&1 \\ \end{array}}\right]}^{-1}}\left[ {\begin{array}{c} 1\\ 1\\ 1\\ 1\\ 1\\ \end{array}}\right]\]
\[\left[ {\begin{array}{l} x_1\\ x_2\\ x_3\\ x_4\\ x_5\\ \end{array}}\right]={\frac{c}{394}}\left[ {\begin{array}{rrrrr} 548&-180&-160&-150&-144 \\ -120&501&-80&-75&-72 \\ -80&-60&472&-50&-48 \\ -60&-45&-40&455&-36 \\ -48&-36&-32&-30&444 \\\end{array}}\right]\left[ {\begin{array}{c} 1\\ 1\\ 1\\ 1\\ 1\\ \end{array}}\right]\] \[\left[{\begin{array}{l} {x_1} \\ {x_2} \\ {x_3} \\ {x_4} \\ {x_5} \\ \end{array}}\right]={\frac{c}{197}}\left[ {\begin{array}{r} -43 \\ 77 \\ 117 \\ 137 \\ 149 \\ \end{array}}\right].\]
If the cost \(c\) is chosen to be \(\frac{197}{4} = 49\frac{1}{4}\), this yields the sample solution found by rote in the Pamiers manuscript, as summarized above.
Randy K. Schwartz (Schoolcraft College), "'He Advanced Him 200 Lambs of Gold': The Pamiers Manuscript - Appendix B: Solutions," Convergence (July 2012), DOI:10.4169/loci003888




