- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Limit Points and Connected Sets in the Plane - Mullikan's Nautilus
In October 1919 the renowned mathematician R. L. Moore read a paper written by his third doctoral student Anna M. Mullikin before an AMS meeting at Columbia University in New York City. Titled “A countable collection of mutually exclusive closed point sets with connected sum,” it presented a clever yet fairly simple example that Miss Mullikin constructed during her first year under Moore’s tutelage at the University of Pennsylvania [1, pp. 146-147]. Ultimately the example, which has come to be known as “Mullikin’s nautilus,” constituted the first part of Mullikin’s doctoral dissertation, which was published in the Transactions three years after her first AMS presentation [3].
Mullikin’s nautilus consists of an infinite collection of arcs Mn, for n = 1, 2, 3, … , each composed of four line segments drawn from the x-intercept (1/2n-1, 0) to (1/2n-1, 1/2n-1) , thence to (-1/2n-1, 1/2n-1) and (-1/2n-1, -1/2n-1), and finally to (1, -1/2n-1) . The abscissa of the final point is always x = 1. Figure 1, taken from Mullikin’s dissertation, displays the first three color-coded arcs: M1, M2, and M3. Formally, Mullikin’s nautilus is defined as M = U Mn.
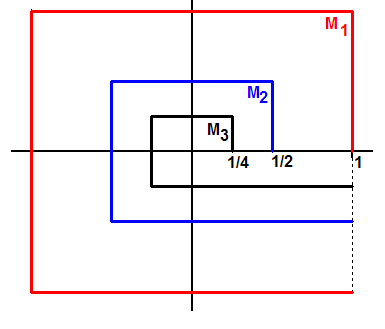
Figure 1
Clearly each arc is connected, but the union M1U M2 U M3 is not. In Figure 1, for instance, the point (1, -1) on M1 cannot be connected to the point (1, -1/4) on M3. We pose the following
FUNDAMENTAL QUESTION: Is Mullikin’s nautilus M = U Mn connected?
The reader might want to hazard a guess now. [Disclosure: this is not an easy issue to resolve.] The answer will be divulged shortly.
David R. Hill and David E. Zitarelli, "Limit Points and Connected Sets in the Plane - Mullikan's Nautilus," Convergence (August 2010)




