- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Peano on Wronskians: A Translation - On the Wronskian Determinant
Peano opened his first article, Sur le déterminant Wronskien, by citing a proposition that most of our students assume to be true, and apparently most mathematicians did as well until 1889.
1. On the Wronskian determinant (by G. Peano, professor at the University of Turin). In nearly all papers, one finds the proposition: If the determinant formed with n functions of the same variable and their derivatives of orders \( 1,\dots,(n-1)\) is identically zero, there is between these functions a homogeneous linear relationship with constant coefficients.
Passage 1
Today, we would say that these functions are linearly dependent.
It is true that if the functions are linearly dependent, their Wronskian is zero. To see this, consider \( y_1 = c_2 y_2 +\cdots + c_n y_n\). By the linearity of the differential, all derivatives of \( y_1,y_2,\dots,y_n\) must obey the exact same relation. This means that the entire first column of the Wronskian can be written as a linear combination of other columns, implying a zero determinant.
The proposition in question, then, asserts the converse of this self-evident theorem, namely that the vanishing of the Wronskian is sufficient to demonstrate linear dependence. To disprove this proposition, Peano gave a simple counterexample. He presented two linearly independent continuous functions \( x(t)\) and \( y(t),\) each with continuous derivatives, that have a zero Wronskian at every real number.
This wording is too general. We offer, in fact, \[ x = t^2 [1+\phi(t)],\quad\quad y = t^2 [1-\phi(t)],\] where \( \phi(t)\) designates a function equal to zero for \( t = 0\), equal to \( 1\) for positive \( t \), to \( -1\) for negative \( t \) (*). One has for \[ t < 0,\quad \phi(t)=-1,\quad x=0,\quad {y=2t^2};\] for \[ t= 0,\quad \phi(t)=0,\quad x=0,\quad {y=0};\] for \[ t > 0,\quad \phi(t)=1,\quad {x=2t^2},\quad {y=0}.\] The functions \( x\) and \( y,\) and their derivatives \[ {x^\prime} = 2t [1+\phi(t)],\quad\quad {y^\prime} = 2t [1-\phi(t)],\] are continuous, and one has, for all values of \( t ,\) \[ \left| \begin{array}{cc} x&y\\x^\prime&y^\prime\\ \end{array} \right| =0 \] But between \( x\) and \( y,\) there is no relation of the expressed form, because the coordinate point \( (x, y) \) does not describe a straight line passing through the origin, but the two half-axes \( ox\) and \( oy.\)
Passage 2
Notice that the argument for linear dependence is very geometric. Peano was using the fact that two functions are linearly dependent if and only if they are constant multiples of each other, since rearrangement of \( c_1 f_1 + c_2 f_2 = 0 \) will give \( f_1 = c\,f_2 \). Hence, if one were to parametrically plot two linearly dependent functions in the \( xy \) plane, one would get a line through the origin of slope \( c\). As Peano stated, his example instead gives the positive \( x\) and positive \( y\) axes when plotted parametrically, as we see here.
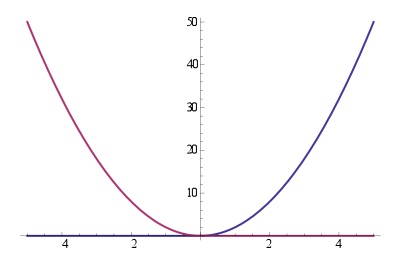
The plots of \( x\) and \( y\) as functions of \( t\).
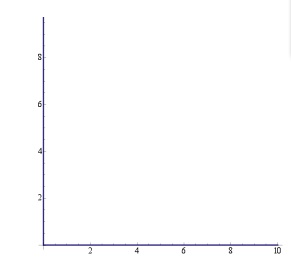
Parametric plot of \( x\) and \( y\).
We see that Peano provided a piecewise-defined formula rather than a single formula for a function \( \phi(t)\) that satisfies the conditions he proposed. Evidently, Mansion must have noted this as he added the following footnote to the above passage, which clearly references a conversation with Peano on the subject:
(*) For example: \[ \phi (t) = \frac{2}{\pi} {\int_0^\infty} \frac{\sin tx}{x}\,dx \] says Mr. Peano. If one wants a more elementary example, we offer \[ \psi (t) = E\left({\frac{1}{1+t^2}}\right),\quad\quad \phi (t) = [1 - \psi (t)]\,{\frac{t+\psi(t)}{{\rm mod.}t+\psi(t)}},\] where \( E(u)\) designates the largest integer less than \( u,\) \( {\rm mod.}t,\) the absolute value of \( t\). (P.M.).
Peano then concluded his note by considering conditions that would make the originally stated proposition true (Passage 1). He gave one such condition, and mused that it would be nice to find others:
The proposal is true if one supposes that there exists no value of \( t\) which cancels all the minors of the last line of the proposed determinant, and perhaps in other cases which would be interesting to investigate.
The phrasing of Peano’s proposed condition is somewhat confusing due to the use of the word “line” (linge). It is unclear whether he was referring to the last row or to the last column.
In 1900, Maxime Bocher indicated that Peano was referring to columns. Bocher added a note to the end of a short article in which he explained his interpretation of Peano’s condition ([B1, p. 121]).
![Bocher [B1, p. 121] Bocher on Peano](/sites/default/files/images/upload_library/46/Peano_on_Wronskians/Picture5.jpg)
Image used with permission from the American Mathematical Society.
A year later, Bocher changed his mind and stated that Peano was referring to the \( (n-1)\times (n-1) \) matrices formed by eliminating the last row and a column of the Wronskian. Notice that these minor determinants are actually just the Wronskians of the functions taken \( (n-1)\) at a time, which might provide a basis for induction. He called this Peano’s Second Theorem ([B3, p. 146]).
![Bocher [B3, p. 146] Bocher on Peano's second theorem](/sites/default/files/images/upload_library/46/Peano_on_Wronskians/Picture6.jpg)
Passage 3. Image used with permission from the American Mathematical Society.
Indeed, mathematicians such as Vivanti ([V]), Bocher ([B1], [B2], [B3], [B4]), and Curtiss ([C]) later offered additional conditions that make the proposition true. The most famous theorem is attributed to Bocher, and states that if the Wronskian of \( n\) analytic functions is zero, then the functions are linearly dependent ([B2], [BD]).
In response to Peano’s request for other interesting conditions that would make the proposal true, Paul Mansion added a second footnote to [P1]:
(*) One can correct the wording of the expressed theorem at the beginning of this note, as we have indicated in our Résume d’analyse, by adding the words: or one of the functions is identically zero. (P.M.).
Passage 4
The passage to which he was referring is from his textbook Résumé du Cours d’Analyse Infinitésimale de l’Université de Gand ([PM]). It is unclear how such an addition would fix the proposition, as neither of Peano’s example functions is identically zero, though if we consider only positive or negative \( t\) values, one of the functions will be identically zero. To see exactly what Mansion means, we turn to the relevant section of his textbook.
Susannah M. Engdahl (Wittenberg University) and Adam E. Parker (Wittenberg University), "Peano on Wronskians: A Translation - On the Wronskian Determinant," Convergence (April 2011), DOI:10.4169/loci003642




