- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Primary Historical Sources in the Classroom: Discrete Mathematics and Computer Science
Contents
Introduction
A traditional method of instruction in the sciences and mathematics involves lecturing, solving template problems within the paradigm, and assigning parallel routine homework questions, as if the logical structure of the subject had always existed, awaiting memorization by our students and ourselves. Definitions are the point of departure, and properties of these defined objects follow without a detailed discussion of the motivating problems and intellectual struggle behind their origin. For example, simply presenting the truth table of an implication (an "if-then'' statement in propositional logic) does little justice to the ancient Greek debate about when a hypothetical proposition (an "if-then'' statement) should be true. Nor is justice done to the concerted attempts to render logic to a suitable computational form in the work of George Boole (1815-1864), Gottlob Frege (1848-1925), Alfred North Whitehead (1861-1947), Bertrand Russell (1872-1970), Ludwig Wittgenstein (1889-1951) or Emil Post (1897-1954), to name a few. Without a study of this historical backdrop, no wonder students are bewildered or bored by the modern proof, via truth tables, that an implication is logically equivalent to a certain inclusive "or'' statement. More than two millennia passed before Russell and Whitehead were able to define an implication in terms of a statement of equivalent deductive power. Many other topics in computer science and discrete mathematics are introduced via announcement, such as the definition of a "tree'' in graph theory as a connected graph with no cycles, or the formula for the sum of squares as \[\sum_{i=1}^{n} i^{\,2} = \frac{n^{3}}{3} + \frac{n^{2}}{2} + \frac{n}{6}%\] and the unenlightening proof of this equality by formal mathematical induction.
 |
|
|
Figure 1. Left to right, logicians Gottlob Frege, Bertrand Russell, and Alfred North Whitehead (Sources: Convergence Portrait Gallery (Frege, Whitehead), Wikimedia Commons (Russell))
As an alternative form of instruction, our series of articles in Loci: Convergence will present sixteen separate curricular modules, each a project for students based on excerpts from primary historical sources, to provide context, motivation and direction for selected topics in discrete mathematics and computer science. Students learn by reading the original work of the pioneers, studying the problems behind modern streamlined definitions, and, together with the instructor, arrive at an understanding of the mathematical concepts and methods that have taken shape over the centuries. Some curricular modules, such as "Discovery of Huffman Codes," are centered around only a few sources and highlight a focused topic of recent development. Others, such as "Deduction Through the Ages: A History of Truth," begin with sources from antiquity and conclude with readings from the twentieth century. Each project module contains excerpts from one or several historical sources, a discussion of the mathematical significance of each selection, and student exercises designed to illuminate the source. Readings and selected exercises could be assigned before the source is discussed in class. In-class activities could include an interpretation of the excerpt, an analysis of how the author's original writing resolves a particular issue, or a discussion of what mathematical techniques have evolved from the source. More challenging student exercises could be assigned after an initial discussion of the source. Instructors should familiarize themselves with the contents of a project, including the exercises, before assignment. Each article contains "Notes to the Instructor" with a summary of the module, prerequisites, and suggestions for classroom use of the material. The instructor should feel free to fashion their own exercises, assign further reading from the source material, if desired, and ask students to write summary papers of their learning, if a writing component is part of the course.
An entire course could be organized around several projects, allowing instruction from historical material without a modern textbook. We have taught several courses in this fashion, including introductory discrete mathematics and an upper-divisional undergraduate combinatorics course. In this way, students witness the development of an entire subject area from primary historical sources and gain a sense of direction to the material. At the end of this introduction we offer several groupings of projects that could be used to teach these courses entirely from our historical modules.
 |
 |
 |
Figure 2. Seventeenth Century mathematicians (left to right) Pierre de Fermat, Blaise Pascal, and Jakob Bernoulli figure prominently in Project 10. (Source: Wikimedia Commons)
What are the advantages of learning from primary historical sources, especially when textbooks present a highly polished view of the subject?
- First, the source adds context. The historical author is often keenly motivated to solve a particular problem or present a novel view on problems with previously ad-hoc or fragmented solutions. We read what the problem was and how it was solved.
- Second, we see the motivation for the development of the subject, and are ourselves motivated to further study.
- Third, we gain a sense of direction to the subject matter, observing where the historical author begins, how a problem is solved, and what subsequent work builds on the solution.
By reading the historical source, often before streamlined notation was developed, the student and instructor are forced to grapple with the verbal meaning of the passage, consider abstract formulations of ideas, and ask "What is an appropriate system of notation for this problem?'' and "What are the key properties to a solution to this problem?'' Answers to these questions often find resolution in present-day definitions, theorems, and algorithms. The thought process required to bridge the gap between the historical and the modern offers an invaluable learning experience that solidifies the concept in the learner's mind. We gain an appreciation of the general setting for modern mathematics by reading the historical author's original statement of the problem and witnessing how key components of the solution have become part of modern definitions. Also, some readers may find it refreshing to learn from a historical description of the problem without the axiomatic constraints of a pre-defined system of calculation. In this way, original sources offer alternative learning strategies, and require no previous knowledge of the subject, but do offer insight into how mathematics arrived at its present state.
We learn more than just the conceptual roots of computer science and mathematics by studying historical sources, but also gain insight into the process of discovery itself by following the thoughts of some of the greatest minds throughout history. We gain an appreciation of the cultural and intellectual setting in which the author was writing. Concerning the benefits of learning from historical sources, students themselves claim the following on end-of-the-semester questionnaires, after studying from these curricular modules:
- "You get answers to questions like 'Where did all of this come from?'''
- "It helps me understand the reason why things were put together like they are.''
- "I like to see where everything comes from and how it works.''
- "You learn the concept.''
- "It makes me care about learning.''
For further reasons to learn from historical sources, see the papers by Barbin [1], Barnett et al [6], Fauvel [8], Guzman [9], and Jankvist [10]. For an analysis of our pedagogy within the context of theoretical frameworks, see [5].
The Projects
What topics are covered in this compendium of projects? Certainly almost all topics in an introductory undergraduate discrete mathematics course, several topics in algorithm design and data structures for computer science, topics in automata theory, combinatorics, and abstract algebra for upper-divisional undergraduate courses, as well as one module in sophomore linear algebra. Each curricular module appears as a separate Loci: Convergence article, although several modules may be used together in the same course, as indicated below. Here is the list of project titles (articles), specific topics contained in each, and the traditional courses in which the project could be used.
1. Deduction through the Ages: A History of Truth
Topics: Elementary propositional logic, truth tables, the truth table of an implication.
Course: Introductory Discrete Mathematics.
2. Sums of Numerical Powers in Discrete Mathematics: Archimedes Sums Squares in the Sand
Topics: Summations, closed formulas, Riemann sums, areas, inequalities, telescoping sums, mathematical induction (optional), systems of linear equations (optional), recursive computation (optional.)
Courses: Introductory Discrete Mathematics, Calculus.
3. Euclid's Algorithm for the Greatest Common Divisor
Topics: Basic division properties of natural numbers, divisors and common divisors, greatest common divisor, basic reasoning, arguments and proofs, formal proof by induction (optional), basic algorithm design and formal description (pseudo-code), reasoning about correctness of algorithms.
Courses: Introductory Discrete Mathematics, Introduction to Computer Science.
4. An Introduction to Symbolic Logic
Topics: Propositional logic, logical connectives, logical equivalence, truth tables, tautologies, inference rules, predicate logic, individual variables and predicates, universal and existential quantifiers, logical equivalence of quantified statements, inference rules in predicate logic.
Course: Introductory Discrete Mathematics.
5. An Introduction to Elementary Set Theory
Topics: Sets, membership and subset, set union and intersection, set complement, the empty set, powerset, Cartesian product, Russell's paradox, functions, composition of functions, one-to-one and onto functions, set equivalence, cardinal numbers, finite and infinite sets, countable and uncountable sets.
Course: Introductory Discrete Mathematics.
6. Computing the Determinant Through the Looking Glass
Topics: Determinants, systems of linear equations, row reduction, elementary operations with matrices.
Course: Linear Algebra.
7. Origins of Boolean Algebra in the Logic of Classes: George Boole, John Venn and C. S. Peirce
Topics: Elementary set operations (union, intersection, relative difference, symmetric difference) and their (algebraic) properties, Venn diagrams, relation of set operations to standard language use, relation of elementary set operations to Boolean algebra, inverse operations (optional), issues related to mathematical notation (optional), changing standards of rigor and proof (optional).
Course: Introductory Discrete Mathematics.
8. Boolean Algebra as an Abstract Structure: Edward V. Huntington and Axiomatization
Topics: Axioms for Boolean algebra, Boolean algebra properties (with proofs), two-valued model of Boolean algebra, axiomatization, consistency, independence.
Courses: Discrete Mathematics (introductory or intermediate), Model Theory, Abstract Algebra.
9. Applications of Boolean Algebra: Claude Shannon and Circuit Design
Topics: Boolean algebra axioms and properties, application of Boolean algebra to design and simplification of circuits, simplification of Boolean expressions, disjunctive normal form, two-valued model of Boolean algebra.
Courses: Introductory Discrete Mathematics.
10. Figurate Numbers and Sums of Numerical Powers: Fermat, Pascal, Bernoulli
Topics: Sums of powers, figurate numbers, binomial coefficients, combination numbers, Pascal's triangle, Bernoulli numbers, recursive definitions and computation, summations and inequalities, counting and geometry, mathematical induction, interplay between discrete sums and calculus.
Courses: Combinatorics, Discrete Mathematics (upper-divisional).
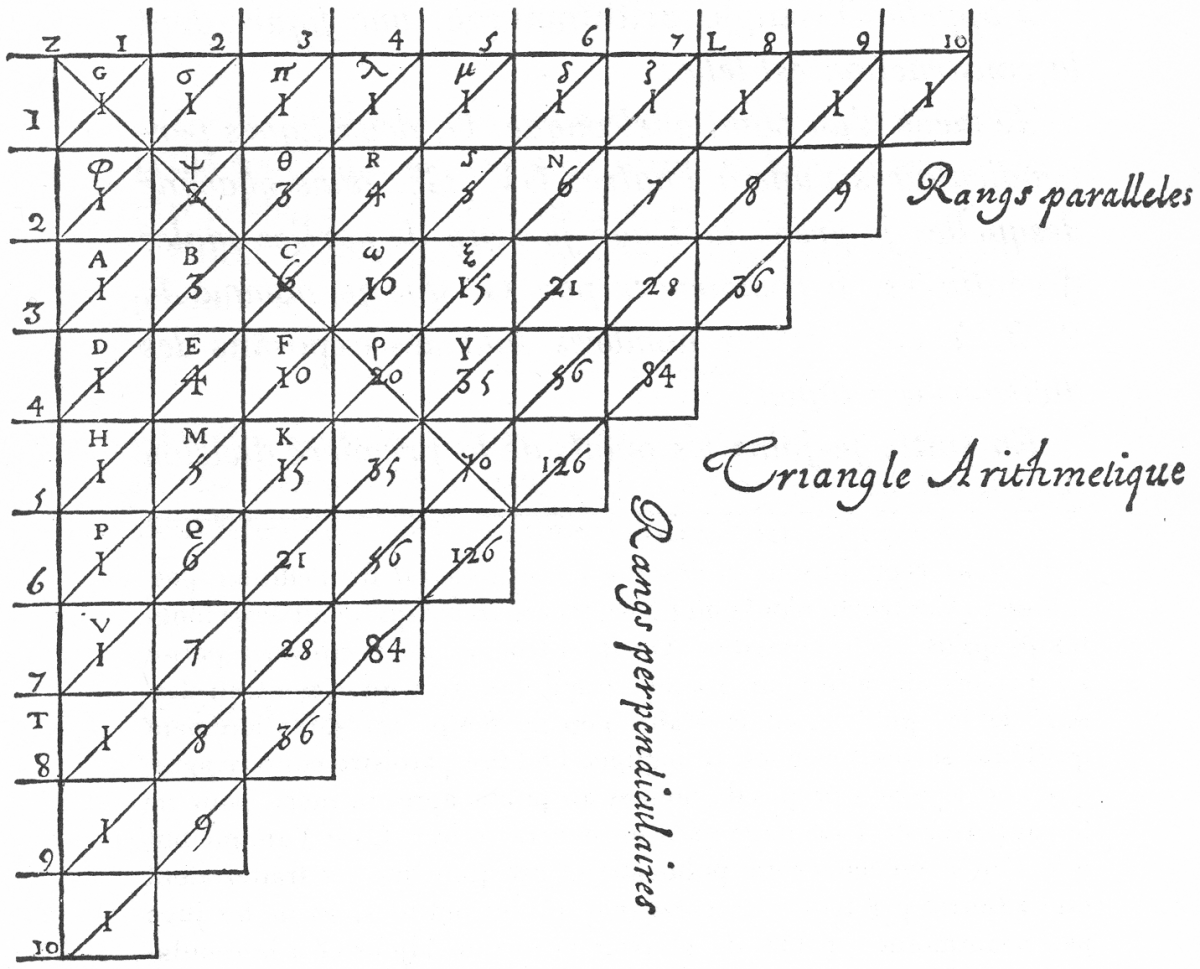
Figure 3. Pascal's "Arithmetical Triangle," as presented in his 1665 Traité du Triangle Arithmetique (Treatise on the Arithmetical Triangle), is an important resource for Project 10 (public domain [7]).
11. Gabriel Lamé's Counting of Triangulations
Topics: Triangulations of a convex polygon, the Catalan numbers, enumeration of triangulations, binomial coefficients.
Courses: Combinatorics, Discrete Mathematics (upper-divisional), Analysis of Algorithms.
12. Networks and Spanning Trees
Topics: Graphs, trees, enumeration of labeled trees, minimal spanning trees, Cayley's formula and Prüfer's symbols for labeled trees, Boruvka's algorithm for finding a minimal spanning tree.
Courses: Graph Theory, Combinatorics, Analysis of Algorithms.
13. Striving for Efficiency in Algorithms: Sorting
Topics: Sorting, quicksort, insertion sort, efficiency of algorithms, stack data structure.
Course: Data Structures and Algorithms.
14. Discovery of Huffman Codes
Topics: Huffman encoding, greedy algorithm, prefix-free code, optimal code, unit of information, amount of information, binary tree.
Course: Data Structures and Algorithms.
Topics: Correctness, partial correctness, algorithms.
Courses: Algorithms, Data Structures, Programming Languages.
16. Regular Languages and Finite Automata
Topics: Regular languages, finite automata, regular expressions, regular events, Kleene's theorem, Kleene's star operation.
Courses: Automata and Formal Languages, Theory of Computation.
Projects by Course
The following subject areas are primary groupings of the projects by some traditional courses:
Discrete Mathematics
1. Deduction through the Ages: A History of Truth
2. Sums of Numerical Powers in Discrete Mathematics: Archimedes Sums Squares in the Sand
3. Euclid's Algorithm for the Greatest Common Divisor
4. An Introduction to Symbolic Logic
5. An Introduction to Elementary Set Theory
7. Origins of Boolean Algebra in the Logic of Classes: George Boole, John Venn and C. S. Peirce
8. Boolean Algebra as an Abstract Structure: Edward V. Huntington and Axiomatization
9. Applications of Boolean Algebra: Claude Shannon and Circuit Design
10. Figurate Numbers and Sums of Numerical Powers: Fermat, Pascal, Bernoulli
11. Gabriel Lamé's Counting of Triangulations
Project: Pascal's Treatise on the Arithmetical Triangle (see [2] or [3])
Linear Algebra
6. Computing the Determinant Through the Looking Glass
Combinatorics
2. Sums of Numerical Powers in Discrete Mathematics: Archimedes Sums Squares in the Sand
10. Figurate Numbers and Sums of Numerical Powers: Fermat, Pascal, Bernoulli
11. Gabriel Lamé's Counting of Triangulations
12. Networks and Spanning Trees
Computer Science
3. Euclid's Algorithm for the Greatest Common Divisor
9. Applications of Boolean Algebra: Claude Shannon and Circuit Design
13. Striving for Efficiency in Algorithms: Sorting
14. Discovery of Huffman Codes
15. Program Correctness
16. Regular Languages and Finite Automata
Courses via Projects
The following projects could be used to teach entire courses from historical modules.
An Introductory Discrete Mathematics Course
1. Deduction through the Ages: A History of Truth
2. Sums of Numerical Powers in Discrete Mathematics: Archimedes Sums Squares in the Sand
3. Euclid's Algorithm for the Greatest Common Divisor
4. An Introduction to Symbolic Logic
5. An Introduction to Elementary Set Theory
Project: Pascal's Treatise on the Arithmetical Triangle (see [2] or [3])
An Upper-Divisional Combinatorics Course
10. Figurate Numbers and Sums of Numerical Powers: Fermat, Pascal, Bernoulli
11. Gabriel Lamé's Counting of Triangulations
12. Networks and Spanning Trees
Further information about these projects, along with the pedagogical approach of teaching from historical sources, can be found from our web resource [4]. This compendium of projects builds on those already in print [2], where the reader will find additional projects related to logic, mathematical induction, combinatorics, graph theory, Turing machines and automata theory. These previous projects can be viewed on a separate web site [3].
Acknowledgment
The development of curricular materials for discrete mathematics has been partially supported by the National Science Foundation's Course, Curriculum and Laboratory Improvement Program under grants DUE-0717752 and DUE-0715392 for which the authors are most appreciative. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Bibliography
[1] Barbin, E., "Histoire et enseignement des mathématiques: Pourquoi? Comment?'' Bulletin AMQ, Vol. XXXVII, 1 (1997), 20-25.
[2] Barnett J., Bezhanishvili G., Leung H., Lodder J., Pengelley D., Ranjan D., "Historical Projects in Discrete Mathematics and Computer Science,'' in Resources for Teaching Discrete Mathematics (Hopkins, B., editor), Mathematical Association of America, Washington DC, 2009, 163-276.
[3] Barnett J., Bezhanishvili G., Leung H., Lodder J., Pengelley D., Ranjan D., Teaching Discrete Mathematics via Primary Historical Sources, http://www.math.nmsu.edu/hist_projects
[4] Barnett J., Bezhanishvili G., Leung H., Lodder J., Pengelley D., Pivkina I., Ranjan D., Learning Discrete Mathematics and Computer Science via Primary Historical Sources, http://www.cs.nmsu.edu/historical-projects/
[5] Barnett, J., Lodder, J., Pengelley, D., "The Pedagogy of Primary Historical Sources in Mathematics: Classroom Practice Meets Theoretical Frameworks,'' to appear in Science and Education.
[6] Barnett, J., Lodder, J., Pengelley, D., Pivkina, I., Ranjan, D., "Designing Student Projects for Teaching and Learning Discrete Mathematics and Computer Science via Primary Historical Sources,'' in Recent Developments on Introducing a Historical Dimension in Mathematics Education, Vol. 78, MAA Notes, Mathematical Association of America, Washington D.C., 2011, pp. 189-201.
[7] B. Pascal, Oeuvres de Blaise Pascal; publiees suivant l'ordre chronologique, avec documents complementaires, introductions et notes (Leon Brunschvicg, Pierre Boutroux, eds.), Hachette, Paris, 1904-14.
[8] Fauvel, J., "Using History in Mathematics,'' For the Learning of Mathematics, 11, 2 (1991), 3-6.
[9] Guzmán, M. de, "Enseñanza de las ciencias y la mathemática,'' Revista Iberoamericana de Education, número 043 (2007), 19-58.
[10] Jankvist, U. T., "A categorization of the 'whys' and 'hows' of using history in mathematics education,'' Educational Studies in Mathematics, 71 (2009), 235-261.
Janet Heine Barnett (Colorado State University Pueblo), Guram Bezhanishvili (New Mexico State University), Hing Leung (New Mexico State University), Jerry Lodder (New Mexico State University), David Pengelley (New Mexico State University), Inna Pivkina (New Mexico State University), Desh Ranjan (Old Dominion University), and Maria Zack (Point Loma Nazarene University), "Primary Historical Sources in the Classroom: Discrete Mathematics and Computer Science," Convergence (July 2013), DOI:10.4169/loci003984






