- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Proofs Without Words and Beyond - PWWs and Mathematical Proof
Two Perspectives on PWWs as Mathematical Proofs
Over the next two sections we construct and apply a framework for appraising the mathematical value of visual proofs. We begin in this section by characterizing two somewhat extreme reactions to visual proofs, which we term the Baroque and Romantic reactions to visual proof. We have chosen to use the terms Baroque and Romantic to characterize these positions partly to avoid any specific allusions to schools of thought in the philosophy of mathematics. These terms evoke the notion of a stance, a response pattern, or an approach rather than a specific and developed school of thought. Our goal is to encourage readers to take a fresh look at visual proof and the activity of proof writing in mathematics, and this goal will not be served as effectively if we try to situate our discussion in the range of ongoing discussions in the philosophy of mathematics. We spend much of the rest of this section exploring the doubts raised about the status of visual proofs from the Baroque perspective. We couch our discussion in this conservative framework because ultimately any defense of the mathematical value of visual proofs will be more persuasive if it is grounded in or at least compatible with a relatively conservative conception of proof in mathematics. By the end of the next section, we will conclude that visual proofs often fail to constitute proofs from the Baroque perspective, but that nonetheless, visual proofs are capable of serving many of the same mathematical aims as traditional proof writing—aims that exceed mere pedagogical value. We also prepare the way for continued philosophical discussion in our final section on multicolor, interactive, and animated PWWs 2.0.
Two Perspectives on Proof I: The Baroque Perspective
We can report anecdotally two common families of reactions that mathematicians have upon encountering PWWs. One reaction is characterized by the thought:
PWWs aren't really proofs, and so a priori they are not convincing.
One might rigidly insist, for example, that a proof must be expressed so as to explicitly draw logical connections between mathematical propositions. Logic operates on the syntax of sentences, so without sentences there can be no proof write-up. One might pick on other logical technicalities in assessing a PWW that depicts a particular case of a general mathematical fact. In mathematics we're usually concerned with general claims, claims about any sum of consecutive cubes or any equilateral triangle, not just the triangle drawn on the board. Some PWWs do a great job of depicting a particular case, but if we wouldn't take the theorem to be proved by examining a single numerical case, why should examining a particular pictorial case change our assessment? In other words, proof by example is no proof at all. Indeed, Fry's PWW (Figure 5) that the sum of the first \(n\) cubes is the square of the sum of the first \(n\) integers depicts only the \(n=3\) case, so the viewer, in the strictest terms, has only been given evidence about one of an infinite range of possible cases:

Figure 5. Fry's Sum of Cubes shows only the case \(n=3.\) [Fry]
Similarly, a given geometric diagram often depicts just one particular choice of an arbitrary point and does not enable inspection of the full range of points in the scope of the theorem, as in Wolf's PWW of Viviani's theorem discussed below and in the [final section]. Something that doesn't address the general phenomenon can't be a proof that the phenomenon holds universally. Because a single example, strictly speaking, leaves a large evidentiary gap, a PWW that depicts a single case of a general phenomenon is not a complete proof and, from this rigid perspective, we should not find it convincing.
For simplicity, we call this first sort of reaction the Baroque response to PWWs. We use the term "Baroque" to indicate the idea that status as a mathematical proof is underwritten by formal correctness, paralleling how a composition's status as a fugue is underwritten by the formal qualities of the music.
Two Perspectives on Proof II: The Romantic Perspective
The second viewpoint is characterized by another thought:
PWWs can be far more rapidly and deeply convincing than traditional, propositional mathematical argumentation, and are therefore (in such cases) perfectly acceptable, even occasionally preferable proofs.
This second family of reactions emphasizes the capacity of a piece of mathematical reasoning to convince and inspire a mathematician. Formal adequacy, i.e., inclusion in the honorific category of proof, is underwritten by apparent evidentiary force—the extent to which an argument should convince a mathematically astute, reasonable audience. If a PWW presents a mathematical idea with sufficient apparent evidentiary force to convince a mathematician of the truth of a statement, why count it as anything other than a proof? Consider, for example, Figure 6, Rick Mabry's proof that \(\sum\limits_{n=1}^{\infty}(\frac{1}{4})^n=\frac{1}{3}:\)

Figure 6. A convincing proof that \((1/4) + (1/4)^2 + (1/4)^3 + \cdots = 1/3.\) [Mabry]
This PWW puts the reader into a frame of mind that enables her to verify the result in a satisfying, convincing, and interesting way. Indeed, we find this PWW to make an extremely elegant, compelling case for the result. For simplicity, we call this second type of reaction the Romantic reaction to PWWs. We use the term "Romantic" to indicate that a good proof is whatever sparks the mathematical intuition or intellect in the right way, prioritizing the mathematical experience over Baroque genre standards.
The Baroque perspective construes proof as a type of evidence distinguished by meeting particular formal constraints, whereas the Romantic perspective construes any evidence that is powerfully and completely compelling to a mathematically astute, reasonable reader as a proof. We find something appealing in both the Baroque and the Romantic approaches to mathematical thought, and we do not intend to adjudicate between these broad approaches to mathematics. However, from a squarely Romantic perspective there is no in-principle challenge to the status of PWWs as proofs; the true Romantic will only ask whether a particular PWW (or traditional wordy proof, for that matter) is effective in producing the target mathematical insight. We work from within the Baroque perspective in exploring and answering challenges to the status of PWWs because generic challenges to the status of PWWs are not native to the Romantic perspective. In the remainder of this section we explain the Euclidean notion of proof and use this notion, which is a further specification of the Baroque framework adopted for the rest of the paper, to develop a critique of the status of visual proofs as genuine mathematical proofs.
A Euclidean Critique of Visual Proof
We take the position, at least for the purposes of our present discussion, that a proof is an argument that meets certain evidentiary and formal or syntactic standards. A proof, as a type of argument, is an abstract object rather than an artifact or other concrete entity. Journal pages, chalk marks, or sequences of sounds are concrete objects or events that can merely express or otherwise encode proofs. A series of words and symbols on a page, or a series of sounds in time, can express a proof, and can express a proof well or poorly. From this perspective, a PWW is an artifact, a collection of marks on a page or screen—at this level of abstraction, at least, no different from a traditional "wordy" proof write-up—and we can ask whether it expresses a proof and, if it does, how well.
By writing up a proof we aim to express or encode a particular deduction. Examination of the notion of proof espoused in textbooks used in Sophomore/Junior-level "introduction to proof" courses yields a perspective that aligns fairly well with the classic Euclidean notion of proof. Consider, for example:
- "The demonstration that a theorem does indeed follow from axioms and previously established theorems is known as a proof." [Goodfriend]
- "To prove a statement is to proceed logically from premises to conclusions." [Lucas]
- "A proof is a series of statements, each of whose validity is based on an axiom or a previously proved theorem." [Morash]
- "A proof is a sequence of irrefutable, logical steps that proceed from axioms and previously proved statements." [Wolf]
Not all textbooks express such straightforwardly Euclidean/Baroque commitments. Consider, for example:
- "A proof is the demonstration of validity of some precise mathematical statement. The demonstration should contain sufficient detail to convince the intended audience of its validity." [Gossett]
- "A proof is a chain of statements leading, implicitly or explicitly, from the axioms to a statement under consideration compelling us to declare that that statement, too, is true." [Gerstein]
These characterizations blur the distinction between proving a statement and convincing or moving an audience. Such characterizations, however, are less typical, and seem to indicate a more Romantic understanding of proof on behalf of their authors.
Adopting a canonical Euclidean perspective, we take a proof to be a deduction of a mathematical result from basic principles of mathematics and other results previously proved, so that one could, in principle, trace a result all the way back to basic mathematical principles (e.g., axioms and definitions).Aside Practicing mathematicians, it would seem from casual survey, tend to understand their completed proofs in these terms. Actual practice, however, admits of some flexibility. Even examining only traditional "wordy" proofs, we can see that the particular form of expression doesn't uniquely determine a particular proof. In practice, we would hesitate to say that two write-ups express different proofs if they make use of the same starting points and lemmas, but derive the lemmas in a different order. And we would also not hesitate to say that write-ups that employ different starting points express different proofs of the same theorem. Intuition does not quite as cleanly settle cases in the middle, where, for example, two write-ups highlight different lemmas, but employ the same starting points. However we settle this issue, any write-up will have to express a minimal amount of ordering: it will have to specify what is supposed to follow from what. A write up of a proof is more than a mere statement of entailment or consequence, but it is at least such a statement.
Written and spoken language serve us well in expressing proofs because their syntactical conventions involve us immediately in ordered expression. This webpage reads left to right, top to bottom. That makes it easy for us to get a reader to go through one thought before another. In the context of reading a proof, this ordering of thoughts can be used to discern relations of entailment. For example, consider the following written proof of Viviani's theorem, a theorem we will revisit several times in this and subsequent sections.
Viviani's Theorem The sum of the lengths of the shortest lines that connect an arbitrary interior point of an equilateral triangle to each of its sides is the same as the height of the triangle.
Proof. Let \(P\) be some point on the boundary or within an equilateral triangle \(ABC\). Label the perpendiculars to the sides from \(P\) as \(p_a\), \(p_b\), and \(p_c\). Note that \(\triangle ABC = \triangle PBC + \triangle PCA + \triangle PAB.\) Let \(h\) be the height and let \(s\) be the length of a side of \(\triangle ABC\). Then, given that the area of a triangle is \(\frac{1}{2}bh\), we have \(\frac{1}{2}sh = \frac{1}{2}sp_a + \frac{1}{2}sp_b + \frac{1}{2}sp_c\). It follows that \(h = p_a + p_b + p_c.\)
In this proof we are first invited to consider a triangle and the three perpendicular lines from an arbitrary interior point. When we say \("\)given that the area of a triangle is \(\frac{1}{2}bh"\) we are pointing to a previous result, one that many of us proved in high school geometry. The remainder of that sentence applies this fact across the equality established above, and then some (suppressed) basic algebra yields the result. The key observation is that \(s\) is a common factor in all terms because \(\triangle ABC\) is equilateral. There are a number of ways to carry out the final algebra: we could multiply both sides of the equation by \(\frac{2}{s}\), we could divide by \(s\) then multiply by 2, or we could multiply by 2 then divide by \(s\). These divergences do not make for a substantially different proof, so it is perfectly reasonable, given the intended audience for the particular write-up, not to detail all the algebra. Importantly, though, because of the verbal medium of this proof write-up, we are led to see exactly what prior mathematical result is relevant to the deduction: the area formula for an arbitrary triangle. Any write-up of this proof of Viviani's theorem, standard or visual, will need to point out the dependence of the final result on this prior mathematical result.
A picture, however, especially when it is accompanied by no explanatory text, presents everything at once, which makes it more challenging to express an identifiable ordering of thoughts or to express what depicted mathematical fact is supposed to be taken as the basis for another. Hence, pictures alone, because of their nature as static, unordered representations, tend to fail to meet Euclidean syntactic or formal standards of proof.
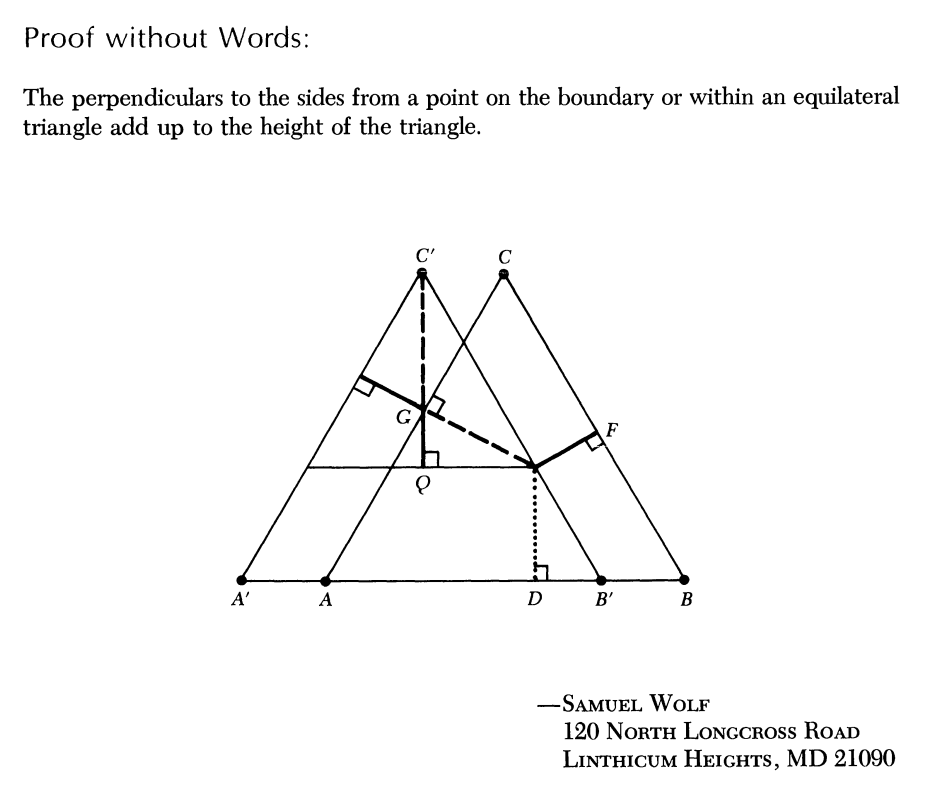
Figure 7. Wolf's Proof Without Words of Viviani's Theorem shows one difficulty of reading a visual proof: the lack of an obvious ordering of thoughts. [Wolf]
The Wolf PWW of Viviani's theorem in Figure 7, for example, is a geometrical diagram that requires the reader to apply her knowledge of geometry to understand how the diagram can be the basis of a proof of the theorem. It does not, strictly speaking, tell the reader what is supposed to follow from what or which geometric principles Wolf intends the reader to apply. (The Wolf PWW of Viviani's theorem appears to encode a very different proof of the theorem, indeed one in which the area formula for a triangle plays no major role.) We discuss the Wolf PWW of Viviani's theorem at greater length in the [final section]. The same phenomenon—failure to precisely encode particular starting points—is present vividly in the PWW in Figure 8:

Figure 8a. Similar to Wolf's PWW in Figure 7, this PWW of the Law of Cosines lacks an obvious ordering of thoughts, though the bolded triangle does suggest the starting point. [Kung]
In this PWW by Sidney Kung, the triangle with sides \(a, b,\) and \(c\) is bolded, indicating that it is the foundation from which the whole figure is constructed. This is a useful visual indicator of logical ordering in the intended proof, a sort of implied visual syntax. After constructing a circle of radius \(a\) around that triangle, the other labels in the figure can be deduced. Trigonometric PWWs like this one, however, tend to draw on other substantial results without explicitly citing those results as we would in a traditional proof. Kung's PWW, for instance, seems to us to rely on the additional, unstated claim that \(xy' =x'y\) as in this figure:

Figure 8b. Diagram for Lemma for Kung's PWW (Figure 8)
If this result is established as a lemma, then the law of cosines follows easily (with one small algebraic step). But the original figure does not encode a whole, self-standing proof. It is effectively left as a puzzle for the reader to figure out what mathematical facts underlie the diagram and verify them for herself. The diagram could be verified in many ways, and the diagram itself doesn't indicate one way over another. Each different verification might yield a different proof, either by operating very differently on the same starting points, or by employing different mathematical facts as starting points. Reliance on the reader's assumed geometrical knowledge isn't the problem, but it is problematic from the perspective of proof writing and proof assessment that these diagrams don't indicate which geometrical facts the reader is intended to bring to bear in rehearsing the proof indicated by the diagram—they fail to indicate starting points. Some concession to the indication of a starting point comes from bolding the central triangle, but that does not eliminate the need for significant interpretation. PWWs like Kung's from 1990 seem to fall more in the realm of pedagogical and recreational mathematics, and within that framework, where the puzzle is actually part of the pedagogical or recreational value of the PWW, ambiguity about starting points is perfectly reasonable. But from the perspective we adopt in assessing whether the PWW is effective as a proof, these sort of PWWs tend to fall short.
Kung's 1990 PWW is also an example of a published PWW that contains sentences. In the ideal case, a visual proof will contain only a statement of the theorem and a diagram or picture, possibly with labels. We draw only a very rough line concerning included text in our definition of "visual proof"; our definition allows the occurrences of words or even sentences as long as they are not "explanatory". We leave the notion of explanation vague, but the basic idea is that a visual proof shouldn't seem like a very incomplete traditional proof supplemented by a diagram; the figure has to do the heavy lifting on its own. So what of Kung's PWW? The first sentence is an algebraic rearrangement of the second sentence, which is the standard statement of the law of cosines—a statement of the theorem to be proved. The diagram purports to be a proof of the first sentence. This sentence is significant or interesting because it is directly equivalent to the law of cosines. Viewing it in this way, Kung's PWW doesn't seem to contain excessive verbiage and may qualify as a visual proof even though it contains sentences. The PWW might have conformed better to the standards we articulate for visual proof if only the top sentence appeared, and if the title was allowed to make the connection between the displayed theorem and the law of cosines. While it may be a borderline case, from our perspective it seems that Kung's PWW is a visual proof. The editors and reviewers of the existing PWW features have displayed substantial flexibility in what counts as a proof without words. We note that our definition of "visual proof" does not strictly imply that all PWWs are visual proofs, though in practice we believe nearly all published PWWs would count as visual proofs under our definition.
Returning to the main line of thought, we note that some PWWs do a great job indicating some sort of ordering, even if it is not always the logical ordering that frames traditional proofs. For example, in Figure 9 the wonderfully elegant PWW of Viviani's theorem by Ken-ichiroh Kawasaki—not unlike the Fry PWW above—indicates a visual starting point and a couple of transformations, in order, from that starting point.
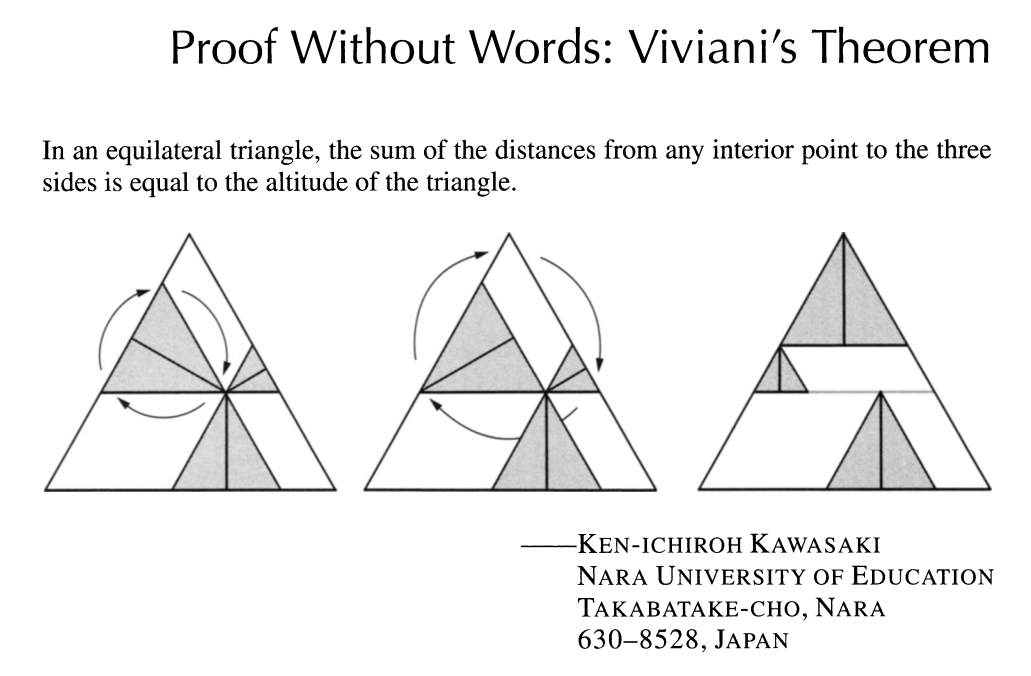
Figure 9. Kawasaki's Proof Without Words of Viviani's Theorem. This PWW has a clearly indicated ordering of some sort. [Kawasaki]
But the visual starting point indicated is not the same as an identifiable progression of propositions that the author of the proof uses to demonstrate the conclusion. A visual starting point for a transformation is very different from a propositional starting point, i.e., a premise to be employed in a deduction. Even this powerfully convincing PWW doesn't obviously encode the sort of ordering necessary for a Euclidean proof.
It appears to be more difficult to visually encode the basic syntactic or formal features that are important from the Baroque perspective. And, although we see no in-principle bar against a visual proof meeting these standards, our own survey of over 80 published PWWs suggests that few PWWs express sufficient argumentative or deductive structure to count as expressing a particular proof, i.e. a particular argument or deduction with particular, unambiguously identifiable starting points, inferences, lemmas, and conclusions. It's not that the PWWs we surveyed didn't present compelling evidence, but rather that the Baroque perspective puts such tight formal constraints on the category of proof that any ambiguity about intended inferential structure counts against a PWW as an unambiguous write-up of a particular deduction. The problem, really, is that one has to interpret the picture in order to discover the deductive structure hidden within, and that interpretive step—when it admits of any significant wiggle room—is at odds with the Euclidean notion of proof. (As we will see in the final section, "Proofs Without Words 2.0," there are ways in which PWWs 2.0 sometimes do a better job at indicating a particular deduction than their PWWs 1.0 counterpart.)
These shortcomings do not, however, correlate with our impression of whether a visual proof is convincing or satisfying. Indeed, the Kawasaki PWW of Viviani's theorem is notable for being both powerfully convincing and difficult to immediately translate into a traditional proof-writing framework. It seems to be an open question where to draw the line between failing to express a proof and failing to clearly express a particular proof. Surely high levels of unclarity push an attempt to write up a proof below the bar and result in a failure to express a proof at all. In general, though, published PWWs clearly express a mathematically compelling idea. To suggest that they fail to express a proof in Euclidean terms does not settle the question of whether a visual proof can express substantial insights and present compelling mathematical evidence for conclusions—even from a Baroque perspective; the Baroque perspective is a stance on proof, not evidence. Proof is a particular, refined way of presenting a special kind of evidence. It should not surprise us if the same general sort of evidence can be presented in other ways.
From the perspective we have constructed, any proof is an argument. In order to express a proof, a figure must, therefore, express an argument. It is important to remember, though, that the expression of the argument is distinct from the argument itself. The argument itself, a structured ordering of propositions, does the work of proving the theorem. The expression of the proof, be it marks on the page, sentences, or pictures, serves to express this argument.
Though inferential relationships are easy to express in sentences, depicting the dependence of a fact upon another fact is difficult. Failure, in general, to meet the syntactic standards of proof—that propositional starting points or premises be clearly designated, for example—does not immediately mean that a visual proof cannot express cogent, insightful mathematical thought and convincing evidence of truth that is allied to the activity and aims of proof-writing. A hard-line Baroque thinker might say that the syntactic or formal standards are actually the core of the evidentiary standards because they help to ensure that the proof is gap-free.Note But there are other purposes and values encoded in the evidentiary standards of proof, and we find it more meaningful to ask whether a visual proof aligns with these purposes and values rather than dumping the whole enterprise because visual proofs don't tend to meet the syntactic or formal standards emphasized in the Baroque approach to proof.
In the case of powerful, convincing visual proofs that don't seem to unambiguously express a particular proof, the hard-line Baroque thinker can take steps to protect the realm of real proofs from incursion. For instance, the natural distinction between the justification and the discovery of a mathematical fact would let the Baroque thinker refer all mathematical justification to proof, but still allow that reasoning falling short of the standards of proof can contribute to mathematical discovery. Discovery (and rediscovery in the classroom setting) is critical to the practice and advancement of mathematics, so this limited role would still present substantial value for visual proofs.
Even if ultimately correct, this hard-line perspective has to contend with differences between visual proofs and other sorts of non-proof demonstrations that promote mathematical discovery. Unlike the other sorts of things that promote mathematical discovery but fall short of proof, e.g. testing particular numerical cases, visual proofs can align very strongly with an array of values that we would associate with proof, i.e. with the justificatory project in mathematics rather than merely the phenomenon of mathematical discovery.
Even the Baroque perspective has to allow some wiggle room to align itself with the actual practice of mathematics, where proof write-ups, even those published by renowned mathematicians in highly regarded journals, admit of at least a small degree of interpretation. Leaving a little room for interpretation, especially when writing for a particular, limited audience, does not undercut the role of proof in mathematical research. We have to be careful not to take the Baroque perspective so far that it turns out nobody ever writes proofs! When we relax the standard a little bit it becomes interesting to ask whether less canonical forms of proof write-up, like PWWs, can slip through the gap and have a place within—or perhaps just in the neighborhood of—the category of proofs.
Even if a PWW struggles to express clear statements of consequence and inferential ordering, it can illustrate the key idea or main insight that a more completely written-up proof could exploit. And when we return to consider PWWs 2.0 in the final section, we will revisit the Euclidean syntactic or formal standard and discuss ways that interactive and animated PWWs can recover some of the proof-writing syntax/form lost by eschewing prose.
In the next section we turn away from questions about the nature of proof to consider instead the reasons that support our proof-writing practices in mathematics, in effect asking: "why do we care about writing proofs as part of the practice of mathematics?" This question is especially relevant to the discussion and appraisal of the mathematical value of PWWs since they often seem to present ideas of genuine mathematical interest without meeting Euclidean, formal standards of proof.
Tim Doyle (Whitman College), Lauren Kutler (Whitman College), Robin Miller (Whitman College), and Albert Schueller (Whitman College), "Proofs Without Words and Beyond - PWWs and Mathematical Proof," Convergence (August 2014)




