- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Sums of Powers of Positive Integers - Thomas Harriot (c. 1560-1621), England
Thomas Harriot was an English mathematician and scientist who lived in London and worked under the patronage of Sir Walter Raleigh and Henry Percy, Earl of Northumberland. Raleigh sent Harriot on a voyage to the Virginia Colony in 1585-1586, allowing Harriot to put his navigational theory into practice and also to gather extensive notes for his book, A Briefe and True Report of the New Found Land of Virginia, first published in 1588.
Harriot never published any of his mathematical or scientific work, but he left over 5000 manuscript sheets of notes on various topics. In his notes on mathematics, he made much greater use of symbolic notation than his contemporaries and many of his successors, including Fermat and Pascal (see below). He also made frequent use of difference tables, employing them to study Pythagorean triples and, as we shall see, sums of powers of positive integers.
Harriot wrote formulas for sums of squares, cubes, and fourth powers on a manuscript sheet headed “Ad aggregata Z. C. ZZ. et c.” (“For sums of squares, cubes, square-squares, etc.”) (Harriot, folio 240). In this heading, we have substituted Z, C, and ZZ for symbols for squares, cubes, and fourth powers (square-squares) that Harriot probably borrowed from Robert Recorde’s famous algebra book, Whetstone of Witte (1557), and we have substituted “et c.” for the symbol Harriot used for “et cetera”.
Figure 8. Robert Recorde's cossist notation for powers can be seen in the list beginning at lower left and ending in the middle of the righthand page, along with simplified versions written in by a reader. The symbols R for the "roote" (first power), Z for the "square," C for the "cubike" (cube), and ZZ for the "square of squares" (fourth power) are at left. For additional images from Recorde's algebra book, The Whetstone of Witte, see Robert Recorde's Whetstone of Witte in "Mathematical Treasures." (Reproduced by permission of Columbia University Library)
On the preceding manuscript sheet, Harriot wrote three difference tables, one containing a column of squares, another a column of cubes, and a third a column of square-squares (Harriot, f. 239), as shown in Figure 9.
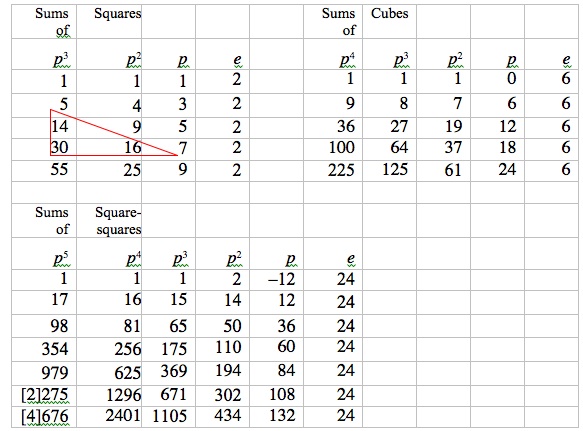
Figure 9. Difference tables for sums of squares, cubes, and square-squares
These tables are called “difference” tables because, for instance, in the triangle of numbers
$$\matrix{ 14 & {}\cr 30 & 16\cr}$$
in the upper lefthand table in Figure 9, the difference between 30 and 14 is 16 (30 – 14 = 16). This difference relationship holds for every such triangle of numbers in the tables in Figure 9 and characterizes these tables as difference tables. If we apply this difference property repeatedly, we see that entries of any column may be summed to obtain entries of the column just to the left. For example, in the two leftmost columns of the upper lefthand table in Figure 9, we see that 14 + 16 + 25 = 55, 5 + 9 + 16 + 25 = 55, 1 + 4 + 9 + 16 + 25 = 55, and 1 + 4 + 9 + 16 = 30. These last two sums are, respectively, the sum of the first five positive integer squares and the sum of the first four positive integer squares, and it follows directly from the definition of difference table and Harriot’s selection of 1 as the first entry of the column labeled p3 and the consecutive positive integer squares as the entries of the column labeled p2 that the nth number in the column labeled p3 is the sum of the first n positive integer squares. (Note that 2 and 3 are superscripts here, rather than exponents.) Likewise, in Harriot’s remaining two difference tables, since the second columns of the tables contain the cubes and fourth powers of successive positive integers, then the first or leftmost columns contain, respectively, the sums of cubes and the sums of fourth powers of successive positive integers.
These difference tables are in fact called “constant” difference tables because the differences become constant in the column labeled “e”. Harriot had general formulas for the entries of constant difference tables and could apply these formulas to the leftmost columns of his tables in Figure 9 to obtain general formulas for sums of squares, cubes, and fourth powers of successive positive integers. Harriot’s formulas, given in terms of the first row of entries in a constant difference table, were as follows (Harriot, ff. 234, 246).
$$\eqalign{&1 v^1 = en - e \cr &\quad \quad \quad + p \cr} $$
$$\eqalign{& 2 v^2 = enn - en \cr & \quad \quad \quad \quad + 2pn - 2p \cr & \quad \quad \quad \quad \quad \quad \; + 2 p^2 \cr}$$
$$\eqalign{ & 6 v^3 = ennn - 0enn - en \cr & \quad \quad \quad \quad + 3pnn - 3pn \cr & \quad \quad \quad \quad \quad \quad \quad + 6 p^2 n - 6 p^2 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 6 p^3 \cr} $$
$$\eqalign{ & 24 v^4 = ennnn + 2ennn - enn - 2en \cr & \quad \quad \quad \quad \quad + 4pnnn - 0pnn - 4pn \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad + 12 p^2 nn - 12 p^2 n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 24 p^3 n - 24 p^3 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; + 24 p^4 \cr} $$
$$\eqalign{ & 120 v^5 = ennnnn + 5ennnn + 5ennn - 5enn - 6en \cr & \quad \quad \quad \quad \quad \quad + 5pnnnn + 10pnnn - 5pnn - 10pn \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 20 p^2 nnn - 0 p^2 nn - 20 p^2 n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 60 p^3 nn - 60 p^3 n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \; + 120 p^4 n - 120 p^4 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad \quad \quad + 120 p^5 \cr} $$
Here, v1 gives the nth entry of the column labeled p, v2 the nth entry of the column labeled p2 , v3 the nth entry of the column labeled p3 , v4 the nth entry of the column labeled p4, and v5 the nth entry of the column labeled p5. For the upper left table in Figure 9, the formula for v3 with e = 2, p = 1, p2 = 1, and p3 = 1 (from the first row of the table) gives
$$\eqalign{ & 6 v^3 = 2nnn - 0 - 2n \cr & \quad \quad \quad \quad + 3nn - 3n \cr & \quad \quad \quad \quad \quad \quad \; + 6n - 6 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \; + 6 \cr} $$
or $$ v^3 = {{2nnn + 3nn + n} \over 6} = {{n(n + 1)(2n + 1)} \over 6},$$
the sum of the squares of the first n positive integers. The formula for v2 with e = 2, p = 1, and p2 = 1 gives
$$\eqalign{ & 2 v^2 = 2nn - 2n \cr & \quad \quad \quad \quad + 2n - 2 \cr & \quad \quad \quad \quad \quad \quad + 2 \cr} $$
or v2 = nn = n2, as expected, and the formula for v1 with e = 2 and p = 1 gives
$$\eqalign{ & 1 v^1 = 2n - 2 \cr & \quad \quad \quad \; + 1 \cr} $$
or v1 = 2n – 1.
The table at upper right in Figure 9 contains cubes in its second column and sums of cubes in its first column. With e = 6, p = 0, p2 = 1, p3 = 1, and p4 = 1, we have
$$\eqalign{ & 6 v^3 = 6nnn - 0 - 6n \cr & \quad \quad \quad \quad \quad \quad + 6n - 6 \cr & \quad \quad \quad \quad \quad \quad \quad \quad + 6 \cr} $$
$$ \Rightarrow \quad v^3 = nnn = n^3, $$
and, for the sum of cubes,
$$\eqalign{ & 24 v^4 = 6nnnn + 12nnn - 6nn - 12n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad + 12nn - 12n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 24n - 24 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\; + 24 \cr} $$
$$ \Rightarrow \quad v^4 = {{6nnnn + 12nnn + 6nn} \over {24}} = {{n^2 (n + 1)^2 } \over 4}.$$
At folio 240, Harriot cited page 25 of Francisco Maurolico’s 1575 Arithmeticorum Libri Duo, copying out the following theorem.
The square of every triangular number is equal to the sum of cubes from unity (one) through the cube of the side of the triangle. (Harriot, f. 240, and Maurolico, p. 25, my translation from Latin to English)
In modern symbols, $$(1 + 2 + 3 + \cdots + n)^2 = 1^3 + 2^3 + 3^3 + \cdots + n^3,$$
or $$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left( {{{n(n + 1)} \over 2}} \right)^2 $$
for every positive integer n.
The remaining table in Figure 9 contains fourth powers (square-squares) in its second column and sums of fourth powers in its first column. With e = 24, p = – 12, p2 = 2, p3 = 1, p4 = 1, and p5 = 1, we have
$$\eqalign{ & 24 v^4 = 24nnnn + 48nnn - 24nn - 48n \cr & \quad \quad \quad \quad \quad \quad - 48nnn - 0 + 48n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \; + 24nn - 24n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 24n - 24 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; + 24 \cr} $$
$$ \Rightarrow \quad v^4 = nnnn = n^4, $$
and, for the sum of fourth powers, $$\eqalign{ & 120 v^5 = 24nnnnn + 120nnnn + 120nnn - 120nn - 144n \cr & \quad \quad \quad \quad \quad \quad \quad - 60nnnn - 120nnn + 60nn + 120n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 40nnn - 0 - 40n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad + 60nn - 60n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 120n - 120 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad + 120 \cr} $$
implying that $$ v^5 = {{24nnnnn + 60nnnn + 40nnn - 4n} \over {120}} = {{n^5 } \over 5} + {{n^4 } \over 2} + {{n^3 } \over 3} - {n \over {30}}.$$
(In all of these computations, the exponents on n are modern. Harriot always wrote, for instance, nnn where we would write n3.)
When Harriot listed his resulting formulas for sums of units, positive integers, squares, cubes, and square-squares, he replaced v0, v1, v2, v3, and v4 with “s” (for sum) followed by, respectively, a dot, line segment, small square, small cube, and his square-square symbol from Recorde. He recorded his formula for the sum of squares, for instance, as s (square) : 6 = 2nnn + 3nn + 1n. Although the computations are long, they are easy and Harriot did not show as much work as we do. He had already done the hard work of deriving the formulas for entries of constant difference tables. For the sum of cubes, for instance, at folio 239 Harriot wrote only
$$\eqalign{ & 6nnnn + 12nnn - 6nn - 12n \cr & \quad \quad \quad \quad \quad \quad + 12nn - 12n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad + 24n \cr} $$
_____________________________________________
$$6nnnn + 12nnn + 6nn + 0n$$
and also checked that his formula for v4 with e = 6, p = 0, p2= 1, p3 = 1, p4 = 1, and n = 5 would give the correct fifth-row value of 225, before recording his final result at folio 240.
At folio 239, the manuscript sheet on which the difference tables in Figure 9 appear, Harriot cited three pages from Maurolico’s Arithmeticorum Libri Duo, pages 52, 63, and 67. What these three pages have in common is a list of the first five differences of the fourth powers, 1 (= 14 – 04), 15 (= 24 – 14), 65, 175, and 369 = (54 – 44), which Harriot copied onto folio 239. Although Harriot himself noted at folio 154 of the same manuscript volume that differences of squares, cubes, and fourth and higher powers are eventually constant and illustrated this property in Figure 9, his citations at folio 239 indicate that he may have hit upon the insight that a column of squares, cubes, or fourth powers could be extended to a constant difference table while studying Maurolico’s Arithmetic.
The English mathematician Henry Briggs (1561-1631), famous for his co-invention of logarithms with John Napier, lived in London at the same time as Harriot. Briggs noted in his 1624 Arithmetica Logarithmica that differences of squares, cubes, and fourth and higher powers are eventually constant (Briggs, pp. 29-30, or Hutton, pp. 386-387), but did not extend his observation to formulas for sums of these powers. We have never found any evidence of contact between Briggs and Harriot. After Harriot’s death, Briggs notified Johann Kepler in 1625 of the impending publication of some of Harriot’s work (Frisch, pp. 661-662) and later, in 1630 or slightly earlier, praised Harriot’s work on “solid angles” or spherical trigonometry (Hakewill, pp. 263-264), but never referred to any other work of Harriot’s.
Exercise 13: Write a constant difference table in which the second column from the left contains fifth powers and the leftmost column contains sums of fifth powers beginning with 1. Include at least four rows. (You’ll need at least seven entries in the second column in order to obtain at least two copies of the constant difference, 120, in the rightmost column only by taking differences.) Use Harriot’s formula for v6, the nth entry of your leftmost column (the column labeled p6), to obtain a formula for the sum of the first n fifth powers in terms of the positive integer n.
$$\eqalign{ 720 v^6 & = ennnnnn + 9ennnnn + 25ennnn + 15ennn - 26enn - 24en \cr & \quad \quad \quad \quad + 6pnnnnn + 30pnnnn + 30pnnn - 30pnn - 36pn \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \, + 30 p^2 nnnn + 60 p^2 nnn - 30 p^2 nn - 60 p^2 n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 120 p^3 nnn - 0 p^3 nn - 120 p^3 n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad\quad \; \; + 360 p^4 nn - 360 p^4 n \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\quad \;\quad \quad\quad \quad \;\; + 720 p^5 \,n - 720 p^5 \cr & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;\; + 720 p^6 \cr}$$
Exercise 14: In order to use Harriot’s method to obtain a formula for the sum of the first n sixth powers, we would need both a constant difference table with leftmost column containing the first few sums of sixth powers and a formula for v7, the nth entry of the leftmost column of an eight-column constant difference table, in terms of the entries, p7, p6, p5, p4, p3, p2, p, and e, of the first row of the constant difference table. Write formulas for v5, v6, and v7 by noting the pattern in the following formulas for v1, v2, v3, and v4:
$$v^1 = (n - 1)e + p,$$
$$v^2 = {{n(n - 1)} \over 2}e + (n - 1)p + p^2,$$
$$ v^3 = {{(n + 1)n(n - 1)} \over {3 \cdot 2}}e + {{n(n - 1)} \over 2}p + (n - 1) p^2 + p^3,$$
and $$ v^4 = {{(n + 2)(n + 1)n(n - 1)} \over {4 \cdot 3 \cdot 2}}e + {{(n + 1)n(n - 1)} \over {3 \cdot 2}}p + {{n(n - 1)} \over 2} p^2 + (n - 1) p^3 + p^4.$$
Solutions to these exercises are available by clicking here.
Janet Beery (University of Redlands), "Sums of Powers of Positive Integers - Thomas Harriot (c. 1560-1621), England," Convergence (July 2010), DOI:10.4169/loci003284





