- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Teaching the Fundamental Theorem of Calculus: A Historical Reflection - Newton's Proof of the FTC
In this section we shall examine one of Newton's proofs (see note 3.1) of the FTC, taken from Guicciardini [23, p. 185] and included in 1669 in Newton's De analysi per aequationes numero terminorum infinitas (On Analysis by Infinite Series). Modernized versions of Newton's proof, using the Mean Value Theorem for Integrals [20, p. 315], can be found in many modern calculus textbooks. The proofs of Leibniz, Barrow, and Gregory have been amply disseminated. For instance, a version of Newton's proof as well as Barrow's and Leibniz' proofs are discussed in Bressoud [5]. Barrow's proof can be found in his Geometric Lectures [9, Lecture X, Section 11, p. 117] and is also discussed in Struik [41, p. 253]. Leibniz's proof appears in Struik [41, p. 282] and also in Laubenbacher and Pengelley [29, p. 133]. Finally, James Gregory's proof is discussed in Leahy [31, 32].
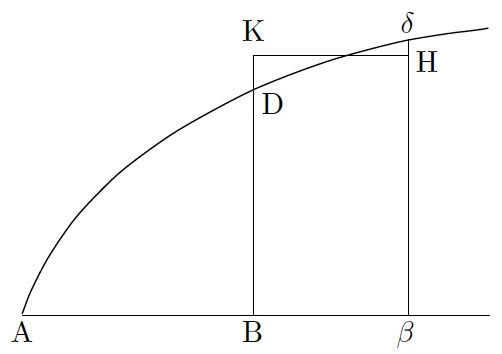
Figure 1. Figure for Newton's Proof of the FTC
Newton considered the curve \(AD\delta\) and set \(AB=x\), \(BD=y\) and \({\rm{area}}\,ABD=z\). He let \(B\beta=o\) be an infinitesimal segment and took \(BK=v\) so that \[vo=\text{area of rectangle}\,B\beta HK={\rm{area}}\,B\beta\delta D\] (see note 3.2). Hence \(A\beta=AB+B\beta=x+o\) and it follows that \[\text{area of region}\,\,A\delta\beta=\text{area of region}\,\,ADB+\text{area of region}\,\,BD\delta\beta\] \[=z+\text{area of rectangle}\,B\beta HK=z+ov.\] If the increment of the area, \(\text{area of region }B\beta\delta D=vo\), is divided by the increment of the abscissa, \(o\), one gets \(v\). Since \(o\) is infinitely small we can assume it to be zero (see note 3.3) so that \(v=y\); that is \(dz/dx=y\).
This argument can be readily expressed in modern mathematical language. If \(\Delta x\not =0\), then \[\frac{\Delta z}{\Delta x}=\frac{1}{\Delta x}\int_{x}^{x+\Delta x}f(u)\,du\] \[=\frac{\Delta x\cdot f(\theta_{x})}{\Delta x}=f(\theta_{x}),\] where \(\theta_{x}\) denotes a real number between \(x\) and \(x+\Delta x\), whose existence is guaranteed by the Mean Value Theorem for Integrals [20, p. 315]. Taking limits and using the continuity of \(y=f(x)\), we have \[\frac{dz}{dx}=\lim_{\Delta x\to 0}\frac{\Delta z}{\Delta x}=\lim_{\Delta x\to 0}f(\theta_{x})=f(x)=y.\] This is Newton's beautiful argument. Notice that besides the use of infinitesimals, he used the additive property of the integral, specifically that \[\text{area of region}\,A\delta\beta=\text{area of region}\,ADB+\text{area of region}\,BD\delta\beta,\] and the interchangeability of ordinates infinitely close to one another.
Barrow's proof [9, Lecture X, Section 11, p.117] is much more geometrical (in keeping with the style of Euclid), but the additivity property is also, as in the case of Newton's proof, crucial to the argument. Similar comments apply to Leibniz's [41, p. 282] and Gregory's [31, p. 9-10; 32, p. 2] proofs. Of Newton, Barrow, Gregory, and Leibniz, the only one who presented an argument for the antiderivative version of the FTC was Leibniz.
3.1. There are several; see Guicciardini [23, p. 183].
3.2. This obviously corresponds to our Mean Value Theorem for Integrals. Newton took an intermediate rectangle whose area lay between the areas of the inscribed and the circumscribed rectangles.
3.3. These are Newton's own words, and they correspond precisely to the statement referred to above; that if two ordinates are infinitely close to one another, either one of them can be taken to be the same as the other. In other words, this is the same as L'Hospital’s Postulate [34, p. 3, I, Demande ou Supposition] about infinitely close ordinates.
Omar A. Hernandez Rodriguez (University of Puerto Rico) and Jorge M. Lopez Fernandez (University of Puerto Rico), "Teaching the Fundamental Theorem of Calculus: A Historical Reflection - Newton's Proof of the FTC," Convergence (January 2012), DOI:10.4169/loci003803




