- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Sagacity of Circles: A History of the Isoperimetric Problem - The Mathematical Problem
Despite its broad implications, the concept of isoperimetry was “naturally Greek.” As Dunham notes, “… even before the time of Euclid the Greeks had enshrined the straight line and the circle as the two indispensable geometric figures, the two shapes constructible with geometric tools … The figure swept out by Euclid’s compass enclosed the maximum area possible for the given perimeter. Is this not further indication of the ideal form the Greeks so admired?” [Dunham, 112]. Pappus himself introduced the notion of isoperimetry in three dimensions by commenting on philosophers “who considered that the creator gave the universe the form of a sphere because that was the most beautiful of all shapes also asserted that the sphere is the greatest of all solid figures which have their surfaces equal” [Heath, 394]. Together with Pappus’s famous preface, isoperimetry was firmly established not as an isolated topic in ancient geometry, but rather as indicative of the grander scheme of the universe and the logic of the natural world.
In its most basic form, the isoperimetric problem asks the geometer “to determine, from among all curves of the same perimeter, the one enclosing the largest area” [Dunham, 104]. To many persons, the notion that the circle encloses the greatest area or even that different shapes of the same perimeter would have different areas seems paradoxical. At first glance, it may not be readily obvious that the last shape of the following four is the greatest in area.

Figure 1. Isoperimetric shapes, from [Wells, 123].
Indeed, in his mathematical commentaries of the fifth century C.E., the philosopher Proclus described geographers “who [wrongly] inferred the size of cities from their perimeters” and of “members of communistic societies in his own time who cheated their fellow-members by giving them land of greater perimeter but less area than the plots which they took themselves” [Heath, 206-7]. It is quite simple to prove that of all rectangles of the same perimeter that which encloses the greatest area is a square (see Fig. 2), however for polygons of greater and greater numbers of sides, the problem becomes less straightforward. The development of the isoperimetric theorem, therefore, was a problem not for myth or history, but for successive generations of mathematicians and geometers.
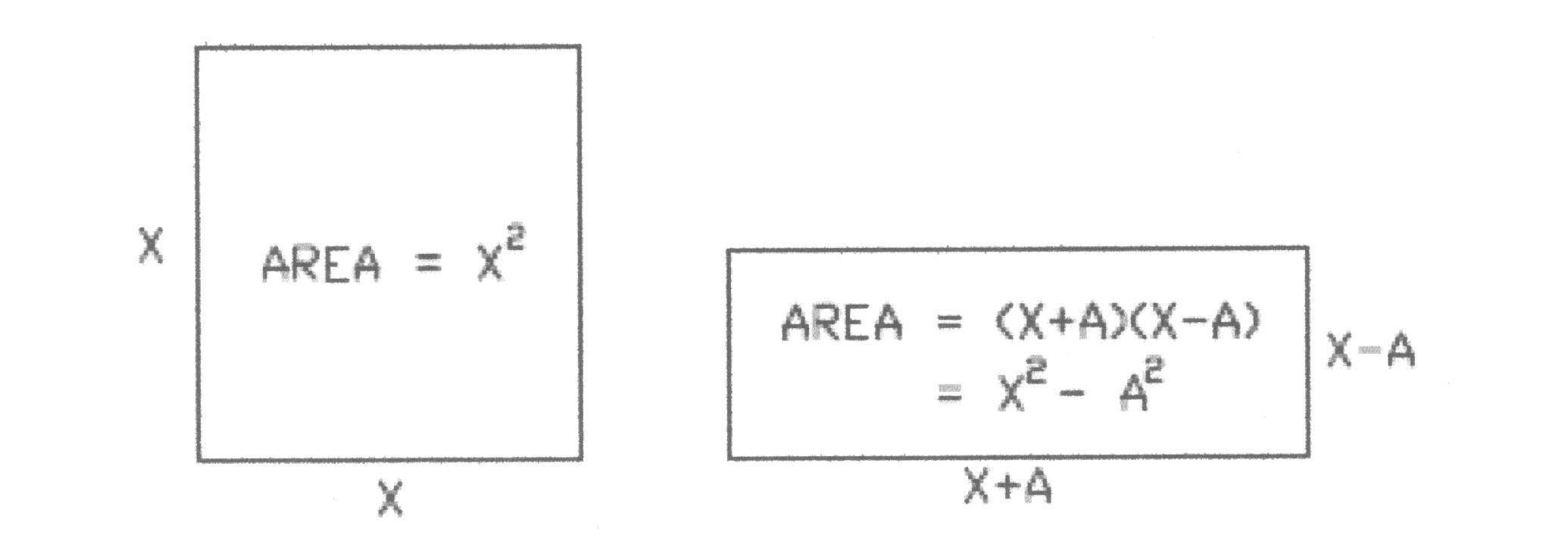
Figure 2. Comparative areas of a square and rectangle [Dunham, 105]
Jennifer Wiegert, "The Sagacity of Circles: A History of the Isoperimetric Problem - The Mathematical Problem," Convergence (July 2010)




