- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Determining r/R
In addition to the periods of the planets, ancient astronomers observed two other gross features of their motions—the lengths and times (durations) of their retrograde arcs. For a single planet the length and time of its retrograde arcs vary somewhat; the following table gives approximate average values that appear to be close to those known to Ptolemy [18].
|
|
Length |
Time (days) |
|
Mercury |
12° |
20 |
|
Venus |
15° |
40 |
|
Mars |
16° |
72 |
|
Jupiter |
10° |
120 |
|
Saturn |
7° |
140 |
Table 2
Revisiting Figure 6, we see that fixing T and S and varying the ratio r/R changes the lengths of the retrograde arcs. Larger values of r/R result in larger retrograde arcs, while smaller ones result in smaller arcs or sometimes none at all. This suggests that data like that found in Table 2 might be used to determine the ratio r/R.
According to [18], ancient astronomers may have used such data, plus a little trigonometry, to find an initial estimate of the ratio r/R for each planet. For the outer planets—Mars, Jupiter, and Saturn—this method of determining r/R is somewhat similar to the method actually used by Ptolemy in the Almagest. For the inner planets—Mercury and Venus—Ptolemy in the Almagest computed this parameter by a quite different method which involved using the planet’s so-called “greatest elongation” from the sun.
To compute r/R by using the data in Table 2, we start at a time when the epicycle center, the planet, and the earth are all in a straight line, with the planet P at the point P[0] on the epicycle (see Figure 7).
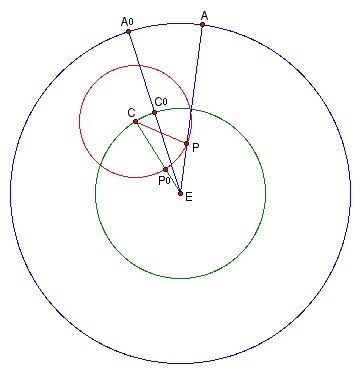
In the figure, C0 is the location of the epicycle center at this time and A0 is the location of the apparent planet on the ecliptic. At this point the planet is in the middle of its retrograde arc. Animating Figure 7 shows the planet’s motion from the middle of the retrograde arc until the end. At that point C represents the new location of the epicycle center and A represents the new location of the apparent planet. Trigonometry now enters the picture, as r is side CP and R is side EC of triangle ECP; thus to find the ratio r/R, we must solve the triangle ECP for the ratio of its sides CP/EC.
Since the planet moves uniformly on the epicycle, the arc P0P has measure equal to the synodic rate of the planet (see Table 1 in Section 6) multiplied by half the time of its retrograde arc given in Table 2 above. Since arc P0P and angle P0CP have the same measure, this determines angle C in triangle ECP. Similarly, since the epicycle center moves uniformly on the deferent, arc C0C has measure equal to the sidereal rate multiplied by half the time of the retrograde arc. This determines angle C0EC which forms part of angle E in triangle ECP. Finally, arc A0A is by definition half of the planet’s retrograde arc; thus its measure is known from Table 2 above. This determines angle A0EP; adding this to angle C0EC gives angle E in triangle ECP. Altogether we have found angles C and E in triangle ECP; subtracting their sum from 180° determines angle P. Using the Law of Sines we can now solve the triangle for the ratio CP/EC.
As an illustration of this method we show the computations for the planet Mars, using modern trigonometry and notation.
Example: Mars
From Table 2, we get the retrograde arc data: (1/2)length = 8° and (1/2)time = 36 days.
From Table 1, we find that the synodic rate is 0.462°/day and the sidereal rate is 0.524°/day.
Angle ECP = arc P0P = (synodic rate) x (1/2)time = 16.6°.
Angle C0EC = arc C0C = (sidereal rate) x (1/2)time = 18.9°.
Angle A0EP = arc A0A = (1/2)length = 8°.
Angle PEC = the sum of angles C0EC and A0EP = 26.9°.
Angle CPE = 180° minus the sum of angles PEC and ECP = 136.5°.
By the Law of Sines, r/R = CP/EC = sine(PEC)/sine(CPE) = 0.66.
Exericise: Use the data in Tables 1 and 2 to find r/R for Mercury, Venus, Jupiter, and Saturn. (Answers are given in Table 3 of Section 8.)
Sandra M. Caravella (New Jersey City University), "Triangles in the Sky: Trigonometry and Early Theories of Planetary Motion - Determining r/R," Convergence (August 2010), DOI:10.4169/loci003120




