- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Using Problems from the History of Mathematics - Students as Mathematical Archaeologists
Students can be placed in the role of mathematical archaeologists and led to discoveries. Assume that the class has discussed numeration systems including the sexagesimal Babylonian cuneiform system. They are presented with a facsimile of the face of a clay tablet from the Yale Babylonian Collection (7289):
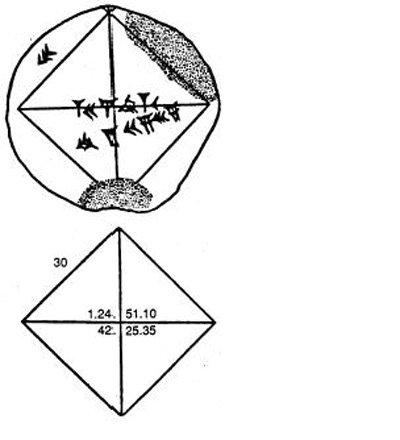
If recognized as numerals, the symbols along the horizontal diagonal can be translated as 1, 24, 51, 10. Babylonian numerals possess a positional value. Thus, if the 1 is interpreted as one unit, the remaining numerals represent fractional components of the number represented, namely, 24/60, 51/602 and 10/603. When the numbers are combined, the mystery number is found to be 1.414 212 9.... It approximates √2 to six decimal places--impressive accuracy for 2000 B.C.E.! Two discoveries emanate from this example: the ancient Babylonians performed geometric constructions similar to those in use today, and they had a proficient technique for the extraction of square roots. Babylonian accuracy in the extraction of square roots prompts further investigation by students--just how did they do it?
Cultural and sociological information can be obtained from the solutions to historical problems. For example, the height of the mast of an Egyptian ship for the period 250 B.C.E. can be found:
- If it is said to you, “Have a sailcloth made for the ships” and it is further said, "Allow 1000 cloth cubits (square cubits) for one sail and have the ratio of the height of the sail to its width as 1 to 1 1/2." What is the height of the sail? (1 cubit = 20 inches) [Answer: 25.8 cubits]
Similarly, the size of a loaf of bread in fifteenth-century Venice can be deduced:
- When a bushel of wheat is worth 8 lire, the bakers make a loaf of bread weighing 6 ounces; required the number of ounces in the weight of a loaf when wheat is worth 5 lire a bushel. [Answer: 9 3/5 ounces]
Or the hourly wages (of a twelve-hour workday) for a man in post-Civil War America can be determined:
- A gentleman received $4 a day for his labor, and pays $8 a week for his board; at the expiration of 10 weeks he has saved $144; required the number of idle and working days. [Answer: 14 idle days and 56 working days]
Frank Swetz (The Pennsylvania State University), "Using Problems from the History of Mathematics - Students as Mathematical Archaeologists," Convergence (June 2010), DOI:10.4169/loci002055




