- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Van Schooten's Ruler Constructions - Solution to Problem IV
Problem IV: Above a given indefinitely long straight line, to construct a perpendicular.
Construction: Conceive the given straight line as going through points A and B, and a perpendicular is to be constructed above it; make BC equal to AB [along the same line] and from B draw BD, making with AB any angle whatsoever, and locate D on that line so that it equals BA or BC, and draw the line from point D through point C. If in that line CF is made equal to CA, and in the line ABC, CE is made equal to CD, I say joining EF makes it be perpendicular to AB.
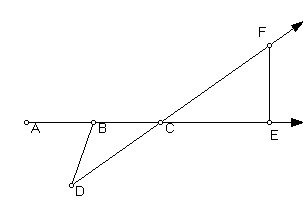
This may be van Schooten’s trickiest construction. The key to the proof of correctness is to note that the points A, C and D are all the same distance from B, so they lie on a circle centered at B and with AC as a diameter. This makes angle ADC a right angle. Now you only have to figure out why angle CEF is also a right angle.
Next:
C. Edward Sandifer, "Van Schooten's Ruler Constructions - Solution to Problem IV," Convergence (August 2010)




