- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Wibold's Ludus Regularis, a 10th Century Board Game - Virtues - Outcomes
The Ludus Regularis
Wibold likely invented his dice game while he was archdeacon at Noyon, France, in the mid tenth century. Canon law forbade clerics to engage in gambling because of the vices associated with it. But Wibold had the idea to co-opt the temptation of gambling and turn it to the promotion of and instruction in virtuous living, thereby permitting clerics to take part in a pleasurable activity while at the same time improving themselves. The game is called both Ludus regularis seu clericalis (the canonical or clerical game) and Alea regularis contra alea secularis (the canonical game of dice as opposed to the secular game of dice). The rules of the game in the words of Wibold himself were preserved by the historian Balderic in the same Chronicon (Chronicle) mentioned above.
Our excerpt of Wibold's account begins with a reference to the canons listed in the section, "Concerning the Use of Dice," and justifies his creation of the game:
. . . Therefore because the same [canonical] rule prohibits clerics to be gamblers---seeing that a game of dice invented by men, perfidious and also deprived of the expectation of good things, is used perversely---as it is a cause of discord, perjuries and other vices: it is very appropriate that having abandoned vices according to the [canonical] rule, [clerics] cast lots for themselves in order to acquire virtues. Therefore it is pleasing that from the same dice play which we have mentioned above, there also be arranged a certain clerical game that for this reason we should call regular, not for the sake of mocking a certain rule, but rather for the sake of training [the players in the cultivation of virtue]. . . .
Association of the Lots with Virtues
Let us consider how Wibold described his numbering of the virtues [2].
Thus set down Charity named with its various offspring, and, as means of governing, let us furnish individually and with each one of the lots of the die [their] corresponding numbers, lest one be unable to discover what is being associated by this [method]; then examine that [lot], and here is shown what is possible. (See Table 1, below.)
Accordingly from the first [row] putting the ones first, and proceeding through the twos and the others up to the sixes, by means of a three-fold cycle of these [numbers] among themselves, it contains the Twenty Daughters of the Holy Mother, and it ends with Wisdom. And afterwards the twos starting with Remorse, fifteen of them to Reverence; from this the threes, from the first, Piety, 10 [of them], to Exomologesis (see note 5); and thus the fours from Maturity, 6 [of them], to Lamentation; with likewise the fives, from Cheerfulness, bringing in 3 [of them]; it is concluded at the end by Self-control. Indeed the last, composed of sixes, as the first, rejoices in simplicity; it possesses the guardian of the virtues, Humility. Which all at once together become 56.
And if we consider more carefully, we shall see that this progression of numbers, from three ascending to eighteen, brings together the virtues, each of the virtues with its own [mate]. Certainly the first, and the second are joined respectively with the last and the second to last; the third, and the second to last, two each; each among themselves are joined, similarly as the first and last, all the way to the four [groups of] six in the middle; [other groups] comprise three, four or five virtues, and in turn with each other always render [in sum] the number twenty-one. These are therefore
- 3, 4, matched with 17 and 18, respectively: namely, Charity, Faith with Self-control, and Humility;
- 5 and 16, two apiece: which are Hope and Fortitude with Lamentation and Compassion;
- 6 and 15, three apiece: Justice, Peace, and Remorse with Exomologesis, Longing and Cheerfulness;
- 7 and 14, four apiece: Prudence, Chastity, Fear, and Joy with Reverence, Contrition, Constancy, and Understanding;
- 8 and 13, five apiece: Temperance, Mercy, Foresight, Sobriety and Cleverness with Wisdom, Virginity, Mortification, Innocence and Concern;
- 9 and 10, 11 and 12 distinguish six apiece: Obedience, Discretion, Goodness, Satisfaction, Simplicity, and Piety; Perseverance, Modesty, Sweetness, Hospitality, Patience and, of course, Indulgence; with Long-suffering, Gentleness, Economy, Zeal, Prayerfulness, likewise also Judgment; Liberality, Poverty, Mildness, Love, Vigilance and by all means Maturity.

Figure 1. First half of Wibold's Table of Virtues [2] (Source: Google Books)
Enumeration of Outcomes
An examination of Figure 1, or its representation in Table 1, makes clear what Wibold described. The triple of numbers placed to the left of each virtue represents the outcome of a roll of three cubical dice. The number to the right of each virtue is the sum of these same three numbers.
Table 1 permits some speculation as to the appearance of a game board. Two of several possible arrangements appear as Tables 5 and 6 in Possible Game Boards later in this article.
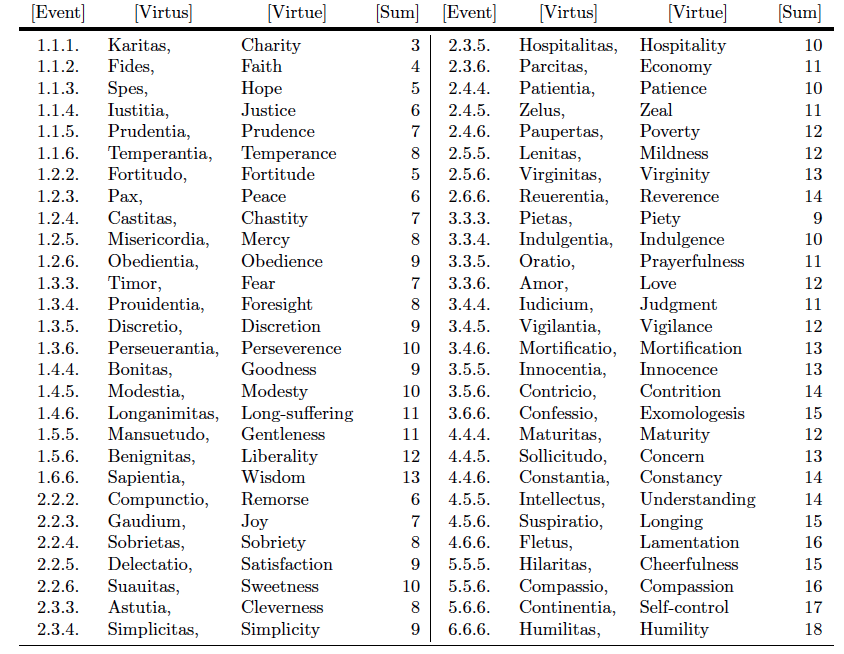
Table 1. Wibold's Table of Virtues, with English translation of virtues added
Suppose we denote the dice, which are clearly cubical, whose faces are marked with the numbers 1, 2, 3, 4, 5, and 6, and which we assume to be distinguishable from one another in some manner, by \(A\), \(B\), and \(C\). Let \(a\), \(b\), and \(c\) or, better, the ordered triple \((a,b,c)\), denote the outcome of the roll of the dice \(A\), \(B\), and \(C\), respectively. Standard dice have been designed for millennia so that opposite sides always sum to \(7.\) Thus there is a one-to-one correspondence between \((a,b,c)\) and the complementary outcome \((7-a,7-b,7-c)\). This observation will be exploited later.
There are then clearly \(6^3=216\) distinct equiprobable outcomes if three (fair) dice are cast. We can enumerate them with the expanded product
\[P=(x+x^2+x^3+x^4+x^5+x^6)(y+y^2+y^3+y^4+y^5+y^6)(z+z^2+z^3+z^4+z^5+z^6).\] A typical term in \(P\) is the product of one term from each of the three factors and, therefore, it must have the form \(x^ay^bz^c\). This term can be understood as representing the outcome \((a,b,c)\).
In the play of the game, however, the three dice are not distinguishable; for instance, the dice rolls \[(1,4,5), (1,5,4), (4,1,5), (4,5,1), (5,1,4), (5,4,1)\] are all considered the same outcome. Thus, to determine the number of ways in which each sum of the faces of dice may be obtained, we replace \(x\), \(y\), and \(z\) in the polynomial above by a single symbol, say \(t\). Each coefficient of the new polynomial \((t+t^2+t^3+t^4+t^5+t^6)^3,\) after being expanded, gives the number of ways of obtaining the sum represented by the corresponding exponent, since \(x^ay^bz^c=t^{a+b+c}\). The expansion of the polynomial in \(t\) is
\begin{equation*}\begin{split}
t^3&+3t^4+6t^5+10t^6+15t^7+21t^8+25t^9+27t^{10}\\&+27t^{11}+25t^{12}+21t^{13}
+15t^{14}+10t^{15}+6t^{16}+3t^{17}+t^{18}.
\end{split}\end{equation*} We can now read off the number of ways to achieve a given total \(n\) as the coefficient of the term \(t^n.\) Thus, for example, there are \(21\) ways to achieve each of the complementary totals of \(8\) or of \(13,\) but only \(10\) ways to achieve each of \(6\) or \(15.\)
Wibold's Cyclic Arrangement
Wibold sought a systematic enumeration of all the lots. (See Figure 1, above.) We see that he made use of a cyclic arrangement in order to enumerate the outcomes of the dice. He constructed his list beginning with the triple \((1,1,1)\) and terminating with the triple \((6,6,6)\) according to the following system:
Every outcome may be represented as a triple \((a,b,c)\) where, because of the indistinguishability of the dice, we always have \(a\leq b\leq c\). Wibold listed the outcomes by using standard lexicographic order: \[(1,1,1)\prec(1,1,2)\prec(1,1,3)\prec\cdots\prec(1,1,6)\prec(1,2,2)\prec\cdots\prec(1,2,6)\prec(1,3,3)\prec\cdots\] He therefore counted a total of 56 triples.
To see this, we might instead note that three types of events can occur:
- All faces are the same;
- two faces are the same but the third is different;
- all faces differ.
It is easy to enumerate the outcomes when all faces show the same: \((1,1,1),\) \((2,2,2),\ldots,(6,6,6),\) six ways in all.
When exactly two faces are the same, we note that three different arrangements of the same numbers occur, say \((a,a,b)\), \((a,b,a)\), \((b,a,a)\), all of which are equivalent. Since there are \(6\) choices for \(a\) and \(5\) for \(b\), each of these three arrangements may be formed in \(6\times5=30\) ways. In all, \(90\) of the \(216\) outcomes are of this type. But, since outcomes of this type are equivalent in sets of \(3,\) there are only \(30\) distinct outcomes of this type.
If all three faces differ, six different permutations may be formed of the numbers: \((a,b,c)\), \((a,c,b)\), \((b,a,c)\), \((b,c,a)\), \((c,a,b)\), \((c,b,a)\), all of which are equivalent outcomes. A permutation of six numbers taken three at a time can be formed in exactly \(6\times 5\times 4=120\) ways. But because the permutations are equivalent in sets of \(6,\) there are only \(20\) distinct outcomes. This gives us a total of \(6+30+20=56\) distinct outcomes.
There is a quicker way to count the distinct outcomes. If we denote by \({}_nW_k\) (with \(W\) chosen to honor Wibold) the number of distinct outcomes when sampling \(k\) items with replacement from a set of size \(n\) where order is ignored, then \[{}_nW_k=\binom{n+k-1}{k}\] (For a discussion of this formula, see [12], for instance.) For Wibold's game, \({}_6W_3=\binom{8}{3}=56\).

Table 2. Ways to achieve each sum with associated multiplicities
Wibold was interested in the sum of the three faces, but he also realized that the opposing face on each cube is complementary; that is, outcome \((a,b,c)\) opposes outcome \((7-a,7-b,7-c)\). Thus it suffices to enumerate outcomes only for values of the sum from \(3\) to \(10.\) Rolls summing from \(11\) to \(18\) can be placed in one-to-one correspondence with those summing from \(10\) to \(3\), respectively, so their counts are correspondingly identical. In Table 2, we use the notation \((a,b,c)_k\) to indicate that there are \(k\) permutations of the numbers \(a\), \(b\), and \(c\).
What may be gleaned from Table 2, above, is that not all ways to achieve a certain sum are equally likely. Let's consider, for example, the sum \(6.\) JUSTICE comes from the outcome \((1,1,4)\) and is given in three ways, PEACE, \((1,2,3),\) in six ways, and REMORSE, \((2,2,2),\) in only one way.
Note
5. Exomologesis refers to the public confession of sins.
Richard Pulskamp (Xavier University) and Daniel Otero (Xavier University), "Wibold's Ludus Regularis, a 10th Century Board Game - Virtues - Outcomes," Convergence (June 2014)




