- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Wibold's Ludus Regularis, a 10th Century Board Game - Was It Ever Played?
Was This Game Ever Played?
The game terminates when each virtue has been acquired by one of the players. It illustrates the so-called "Coupon Collector's Problem." A collector desires to acquire a complete set of coupons where these coupons are obtained by independent random trials. The collector seeks the expected number of trials required and, more generally, the probability distribution of the number of trials.
In Wibold's game, a given trial consists of the roll of the three cubical dice and a roll of the tetrahedral die. There are therefore \(6^3\times 4=216\times 4=864\) distinct equiprobable outcomes. However, a given virtue is acquired only if
- Its corresponding numeric values arrive on the upper faces of the cubical dice.
- Its vowels appear on the upper faces of the cubical dice.
- At least one of its consonants appears on the bottom face of the tetrahedral die.
We illustrate the computation of the probability of obtaining a virtue with several examples.
We saw that PAX corresponds to the outcome \((1,2,3)\). This outcome may be obtained in the following 6 ways in which the cubical dice are rolled:
| A IO AEI | A OU AEI | E EI AEI |
| E OU OUA | I EI UAE | I IO OUA |
All yield the requisite vowel A.
One face of the tetrahedral die contains P, another X. Therefore, the probability of obtaining PAX in a trial is \(\frac{6}{216}\times\frac{2}{4}=\frac{12}{864}\).
In the same manner, consider GAUDIUM. It corresponds to the outcome \((2,3,4)\) which may be obtained in the following 3 ways:
| EI IO AEI | EI OU UAE | IO OU OUA |
Only two outcomes contain an A, an I, and a U twice. Three faces of the tetrahedral die contain one of the consonants D, G, and M. Therefore, the probability of obtaining GAUDIUM in a trial is \(\frac{2}{216}\times\frac{3}{4}=\frac{6}{864}\).
The outcome \((1,1,1)\) corresponding to KARITAS contains the vowels A, E and I. A second roll is specially permitted to obtain the second requisite A. Regardless of choice of die, an A will appear on 4 of the faces. As for K, R, T, and S, the consonants occur on 3 of the faces of the tetrahedral die. Therefore, the probability of obtaining KARITAS in a trial is \(\frac{1}{216}\times\frac{4}{6}\times\frac{3}{4}=\frac{2}{864}\).
Proceeding in this manner, the probability associated with each virtue may be obtained. These probabilities are deduced from Table 3 by dividing each number in the table by 864. The probability that a roll yields no virtue at all (listed as NULL in the Table) is \(\frac{447}{864}\approx 0.52\). This spells trouble for the players of the game since slightly more than half the rolls do not advance the game.

Table 3. Number of outcomes yielding each virtue
Analysis of the Game
Figure 2 illustrates a realization of the game. Note the long periods where the game fails to advance. Repeated simulation of the game shows that the play resolves into three distinct parts: an initial segment, in which virtues are acquired quickly by the players until about 40 of the 56 have been distributed; a middle section during which acqusition of virtues slows down, until only two or three unacquired virtues remains; and a final very slow period of play, extending over hundreds, and even sometimes thousands, of rolls, until the final virtue has been acquired. The reader is invited to try out the applet simulator (see Play the Game!) to confirm this phenomenon for himself or herself.

Figure 2. A typical realization of Wibold's game
The expected number of rolls required to complete the game is given by the integral \[\int_0^\infty\left(1-\prod_{i=1}^m 1-e^{-p_it}\right)\,dt=1656.05\] where here \(m=57\) (the number of possible outcomes) and \(p_i\) is the probability associated with each virtue. For the derivation of this formula, see [10].
A simulation of the game conducted by one of the authors was repeated 10000 times in which the duration of the game was recorded. The relative frequency histogram displayed in Figure 3 shows the result. Here the sample mean of the number of rolls is 1656.126 and the sample standard deviation is 810.536. From these data, the estimated 95th percentile of total rolls is found to be 3222.
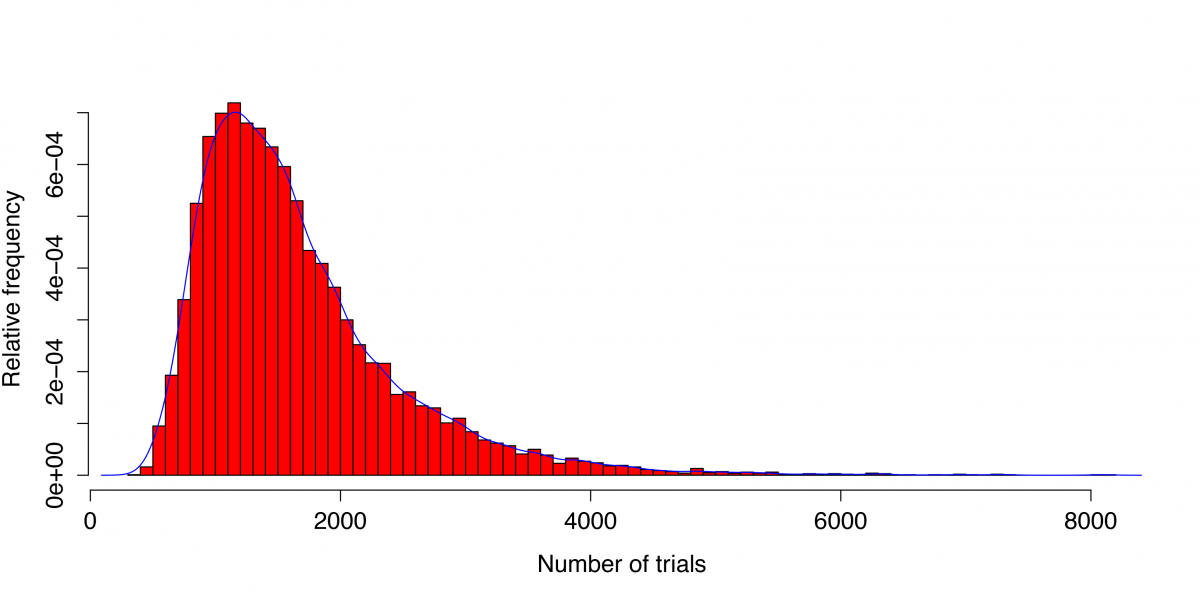
Figure 3. Empirical distribution of the duration of Wibold's game
Analysis of the Simplified Game
If the simplified game is played, a player receives all virtues having the same sum whenever that sum is cast. In the section on the enumeration of outcomes, we saw that there are 16 distinct sums ranging from 3 to 18 and we computed the number of ways that each can be obtained. These are shown in Table 4. The probability of each outcome is the number from the table divided by 216.
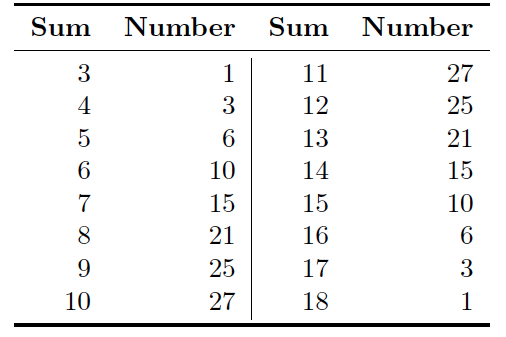
Table 4. Number of ways to obtain each sum
Figure 4 illustrates a realization of this abbreviated game. There is again a somewhat long period where the game fails to advance.
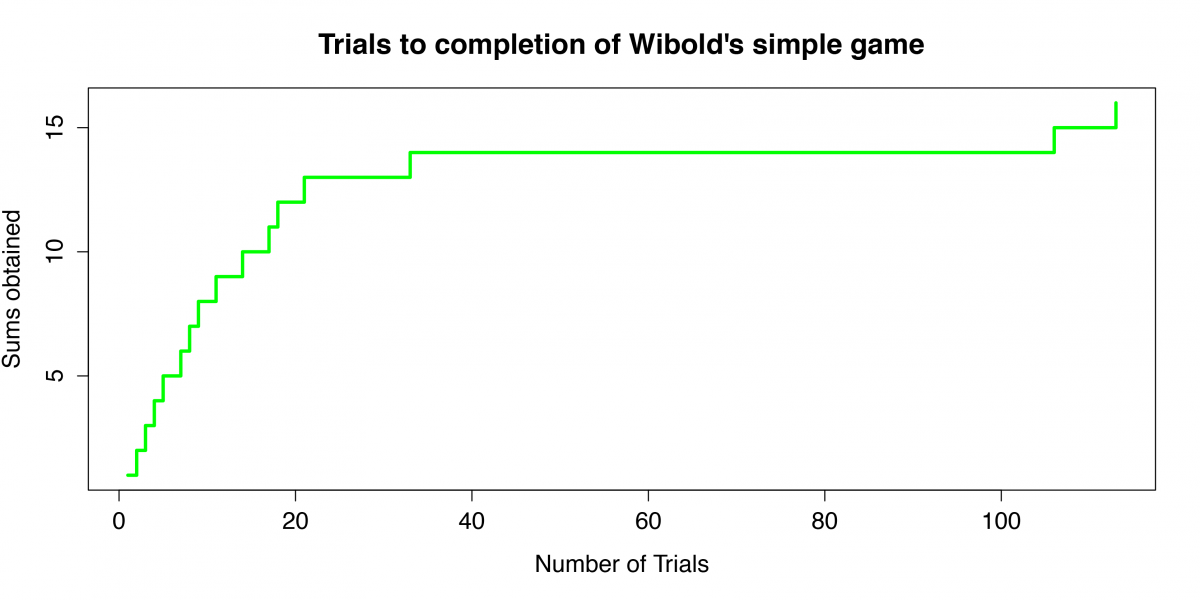
Figure 4. A typical realization of Wibold's simplified game
The expected number of trials is computed to be \[\int_0^\infty 1-\prod_{i=1}^m\left(1-e^{-p_it}\right)\,dt=338.45\] where here \(m=18\) and \(p_i\) is the probability associated with each sum.
A simulation of the simplified game was repeated 10000 times in which the duration of the game was recorded. The relative frequency histogram displayed in Figure 5 shows its result. Here the sample mean of the number of trials is 339.595 and sample standard deviation is 233.200. From these data, the estimated 95th percentile of total rolls is found to be 806.

Figure 5. Empirical distribution of the duration of Wibold's simplified game
If we assume that between 2 and 3 rolls can be cast and the corresponding virtue resolved during each minute of play, the duration of the game can be estimated.

This suggests that the game as Wibold described it was never actually played or, if it was, play was necessarily distributed over several sessions. It is difficult to imagine players devoting ten or more hours of continuous attention to this activity despite its moral benefits. As Figure 2, above, indicates, the bulk of the virtues are acquired within the first hundred rolls. Most of the rest arrive within 500 rolls. The last few however may require thousands more.
The simplified game, on the other hand, could well have been played. Even though the pattern of play is entirely similar to the longer game (Figure 4), its expected duration is one-fifth as long, requiring only a few hours of play.
Richard Pulskamp (Xavier University) and Daniel Otero (Xavier University), "Wibold's Ludus Regularis, a 10th Century Board Game - Was It Ever Played?," Convergence (July 2014)




