- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Exploration: Exponential Functions and Derivatives - Graphing Exponential Functions
General exponential functions, of the form f(x)=Cekx, can be graphed using just two points (x0,y0) and (x1,y1) on the graph of the function.
Tom Leathrum is Associate Professor of Mathematics at Jacksonville State University. He is also an Associate Editor of this Journal.
If the two points are on opposite sides of the x-axis, then there is no graph drawn. This is because of the relationship between the constants, C and k, and the points, (x0,y0) and (x1,y1), on the graph.
In the equation y=Cekx, the two constants C and k determine the shape of the graph. These two values are fixed, given two points (x0,y0) and (x1,y1) on the graph. To see how these two points determine the values of C and k, plug the two points into the equation separately:

Now solve each of these equations for C:
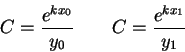
Since both equations represent C in terms of the other variables, set the right hand sides equal --- this eliminates the constant C from the equations:

Now solve this equation for k -- first, rewrite the equation a bit:

Now take natural logarithms on both sides:

This is where it is important that the two points (x0,y0) and (x1,y1) be on the same side of the x-axis -- in other words, that y0 and y1 have the same sign, so that y1/y0 is positive and the logarithm on the left hand side is defined. If y0 and y1 have the same sign (which can be checked with the inequality y0y1>0) then ln(y1/y0) =ln(|y1|)-ln(|y0|) by properties of logarithms, with the absolute values guaranteeing that the logarithms will be defined even if y0 and y1 are negative. Some care must be taken at this point to check the inequality y0y1>0, though, since this expression with the absolute values no longer requires y0 and y1 to have the same sign.
Continuing to solve for k, the equation now looks like:

Solving this algebraically for k:

It is interesting to notice that the above equation resembles the slope of a line.
Now that the value of k is known (from the points (x0,y0) and (x1,y1)), finding C is easier: plug either point into the equation y=Cekx -- plugging in (x0,y0) gives y0=Cekx0. Now divide both sides by ekx0 to solve for C:

These formulas for C and k depend only on the two points (x0,y0) and (x1,y1).
© 2001 by Tom Leathrum -- additional copyright information
Published January 2001
Tom Leathrum, "Exploration: Exponential Functions and Derivatives - Graphing Exponential Functions," Convergence (October 2004)




