- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Intuiting Mathematical Objects using Kinetigrams - Kinetigrams: Dissolution
Over the past five years I have been developing a modeling approach to teaching calculus (Pais, 1997-2001), which emphasizes exploratory problem solving and visualization, and which refocuses and reprioritizes the learning goals of a traditional calculus course to ensure that the course content will be both appealing and useful to pharmacy students. In the process, I have developed several pharmacokinetic modeling situations that I will use in this paper simply because they are close at hand and permit fairly rapid development of the computer graphics that I need to illustrate my ideas. I thank you, my reader, for your indulgence and, since this application context will most likely seem unfamiliar, I ask you to pick the mathematics out of the given context and try to think about how you might do something similar in your own setting. Further, bear in mind that these modeling situations are convenient fictions, and the degree to which they faithfully capture the processes they purport to model is not at issue here.
Here is a clear introductory description of pharmacokinetics from Spitznagel (1992):
|
Pharmacokinetics is the study of the movement of drugs through the human system, from their introduction by ingestion, injection, or other means, to elimination through excretion or metabolism. It makes heavy use of compartment models as found in many differential equations textbooks. Since almost all students take medications from time to time, pharmacokinetics models are something they can easily relate to. For convenience many drugs are taken orally in the form of tablets. With some exceptions, these tablets [dosage forms] are designed to swell and disintegrate rapidly [release], causing the medication to dissolve quickly in the gastrointestinal tract [dissolution]. From there, the medication passes into the bloodstream [absorption], which delivers it to the sites at which it has therapeutic effect. Typically, the drug is removed from the bloodstream by filtration through the kidneys [excretion] or by metabolism in the liver. |
The primary mathematical objects that we will be concerned with are real-valued functions defined on some closed interval [0, a], which will be introduced in the context of modeling the dissolution, absorption, and excretion processes. The displayed argument of each such function will be t, to indicate the time-dependent nature of the process that is being modeled. My main purpose in this section of the paper is to assess some alternative approaches to defining these functions, in terms of Thurston's notion of an effective mathematical communication.
I first distinguish two basic types of definitions: analytic and intuitive. The box below shows an example of the first type. In this context 'dissolution profile' means the shape of the graph of the dissolution function, and 'formulation' means chemical formulation of the drug in dosage form. Also, 'drug dose' refers to the total quantity of medication present in the dosage form (tablet), measured in milligrams. The aim of this definition is to model only the dissolution process occurring in the gastrointestinal (GI) tract, and hence it does not address absorption into the bloodstream.
.
|
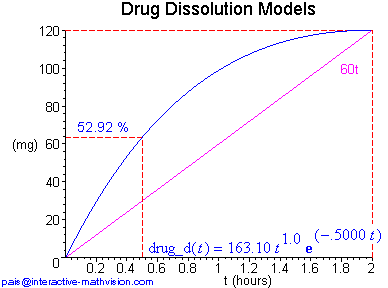
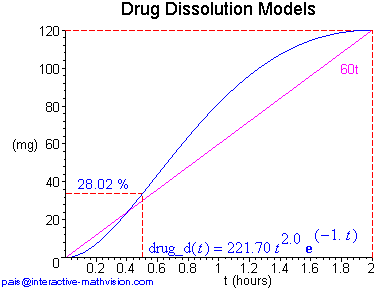
The analytically oriented definition above provides a mathematically precise description, but at this point it provides no intuitive insight into the mathematical objects that it purports to describe, except possibly for those mathematicians who are familiar with how this class of functions looks. So, in a standard development one would next present some specific examples. Here, without all the details, are two examples. In the first one, we let n = 1 and assume our drug dose is 120 mg with a desired time to complete dissolution of 2 hrs. In the second one, this last assumption is the same, but we begin with n = 2.
.
|
For our immediate purposes in this paper, a (mathematical) 'diagram' is an heuristic, 2D, finite, partial representation of mathematical objects, containing both visual (graphical) and analytic (linguistic) components, and organized in such a way as to readily convey information about the new mathematical objects we are trying to develop. Moreover, this conception of diagram provides a crucial intuitive interface to mathematical objects as abstract objects discussed in section 1 of this paper. In each diagram example, above and below, we see both the shape of a Makoid-Banakar function and its corresponding analytic description, together with other pertinent information that can be immediately extracted from each diagram, e.g. the constraint that 120 mg of the drug is dissolved in 2 hrs at the same time as the maximum value of the Makoid-Banakar function, a comparison with uniform dissolution at a rate of 60 mg/hr (the purple line), and the percentage of drug dissolved in the first half hour.
.
|
Our Analytic Definition 1, as is usual with analytically oriented definitions, has as its primary purpose to provide a clear and precise analytic specification using minimal language that is designed to reveal exactly what will be needed in the statement and proof of anticipated theorems. In contrast, our Diagram Examples 1 and 2 are designed to provide the beginning of an intuitive unfolding of the mathematical objects specified by the analytic definition, namely, Makoid-Banakar functions. So, to emphasize the intuitive development over the analytic, we might consider reversing the order of presentation, but this too is not quite what we want. However, if we reflect on Thurston's suggestion that we should try to develop "mathematical language that is effective for the radical purpose of conveying ideas to people who don't already know them," then the notion of some sort of hybrid presentation emerges. I have been experimenting with a hybrid presentation that I call a 'kinetigram definition'. A 'kinetigram' is simply a diagram that changes. Below is an example of a kinetigram definition for Makoid-Banakar functions that incorporates both analytic and intuitive features simultaneously using two adjacent panels, both of which are part of the kinetigram although only Panel 1 happens to have elements that change. Both panels are intended to be simultaneously presented for viewing, with the viewer deciding what to focus on.
Click here for a note on screen resolution and image size.
.
|
What are we looking at? Asking this question is the way I introduce this material to students, and I find that immediately we are all engaged and communicating in a common language. This approach is very tolerant of different learning styles and permits each student to find his or her own point of engagement in a highly nonlinear way that doesn't require suffering through a personally uncongenial, arbitrarily chosen, linear path of access. Furthermore, the great deal of interlinked, constructive variation that is viewable in Panel 1 provides the learner with a very rich medium for personal intuitive unfolding of Makoid-Banakar functions, which goes well beyond merely viewing the individual frames of the movie. Not only are constraints of the model readily extracted from the kinetigram, but more importantly so are a variety of questions and conjectures that lead naturally into an analytic development of the related mathematics.
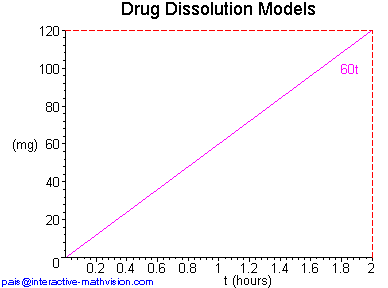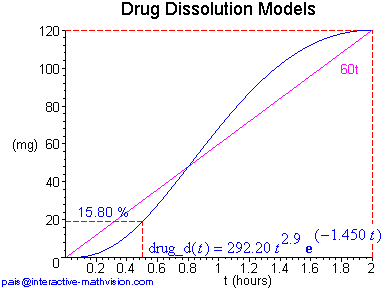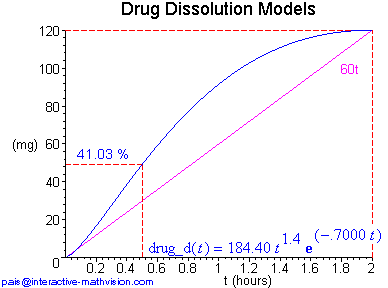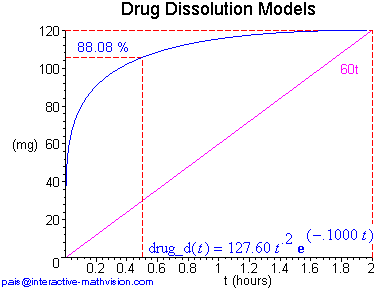
One interesting visual comparison that can be made, since we have several instances of Makoid-Banakar (M-B) functions with both analytic and graphical representations, involves noticing how these different representations relate to one another. For example, we can readily see that when n = 2, 3, 4, the shape of the corresponding M-B function starts out looking like t2, t3, t4, respectively. Furthermore, the smaller n is, the faster the M-B function ramps up. However, although n is clearly related to the shape of the M-B function, the way in which the other constants relate to the shape seems more subtle. Here we have several instances of functions with both analytic description and graph in which the graph conveys much more useful information. This is an important negative fact to understand concerning analytic descriptions. On the other hand, a positive point, which can now be made and further developed with students, is that the power of the analytic description is its usefulness in explicitly capturing and analyzing the information visible in the graph.
At this point I would be remiss if I did not mention David Tall's seminal paper on the role of visualization in calculus. I did not fully apprehend its significance until recently, after I had been working on kinetigrams and began thinking again about the relationship between intuition and rigour in doing and learning mathematics. Here are two particularly relevant passages from pages 110 and 118, respectively:
|
If we are to fill the gap in students' understanding of the calculus, then I hypothesise that we must find a way that is cognitively appealing to the students at the time the study commences [my italics] yet has within it the seeds for understanding the formal subtleties that occur later... By introducing suitably complicated visualizations of mathematical ideas it is possible to give a much broader picture of the ways in which concepts may be realized, thus giving much more powerful intuitions than in a traditional approach. It is possible to design interactive software to allow students to explore mathematical ideas with the dual role of being both immediately appealing to students and also providing foundational concepts on which the ideas can be built... Thus intuition and rigour need not be at odds with each other. By providing a suitably powerful context, intuition naturally leads into the rigour of mathematical proof. |
I think that Kinetigram Definition 1 is an example of an intuitively oriented mathematical definition that can provide beginning students with immediate, cognitively appealing access to the mathematical objects under development. One obvious improvement would be to include some interactivity in the kinetigram, and as a first step I have written the following Java animation player that will permit the website visitor to stop and control the movie in various helpful ways.
| The Java version of Kinetigram Definition 1, Panels 1 and 2: |
|
Next we have an example of a nice kinetigram exercise. In this exercise tif(t) is the 'tangent intercept function' for f(t). Though it is apparently not well-known to calculus teachers, the analysis and graphing of tif(t) can provide a very natural and different way for the student to see an inflection point of f(t).
| Here is the Java Kinetigram Exercise: |
|
John Pais, "Intuiting Mathematical Objects using Kinetigrams - Kinetigrams: Dissolution," Convergence (October 2004)