- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Iterative Methods for Solving Ax = b - Exercises, Part 1: Jacobi and Gauss-Seidel Methods
-
Solve the system
using Jacobi’s Method with the following details:
-
Using x(0) = (0, 0), complete a table like the one below, doing five iterations. Compute the first two iterations
x(1) andx(2) by hand (show your work!), and use the applet to perform the next three iterations.
k x(k) x(true) − x(k) ||error(k)|| 1 −4.000000 − 1.250000 − 1.000000 − 0.750000 1.250000 2 3 4 5
- Do more iterations (don’t write down the details of the results -- that is, don’t make a table for these next iterations) until the applet shows
||error(k)|| = 0.000000. How many iterations are required?
-
- Repeat Exercise 1 with the system
 .
. -
Repeat Exercise 1, using the Gauss-Seidel Method.
-
Repeat Exercise 2, using the Gauss-Seidel Method.
-
Systems (A) and (B) at the right have the same solution. Use both Jacobi's Method and the Gauss-Seidel Method, with three different initial guesses, to solve both systems. Use the applet to do all of the work. For this problem we're interested only in how many iterations are required to get to(A) 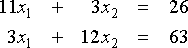
(B) 
||error(k)|| = 0. (The error is not exactly 0, but it rounds to 0 to six digits after the decimal.) Complete a table like the one shown here, in which the first and last results are given. Then answer the questions in a. and b. following the table.
System Initial guess # iterations until
||error(k)|| = 0.000000Jacobi / GS Jacobi GS A (0, 0) 13 7 13 / 7 ≈ 1.857 A (100, − 50) A (− 500, 1000) B (0, 0) B (100, − 50) B (− 500, 1000) 156 79 156 / 79 ≈ 1.975
- Based on the results in the table, comment on which feature seems to have more effect on how quickly we get a good approximation (i.e., how quickly the error goes to 0): the initial guess or the system of equations itself (the matrix A for that system).
- Based on the results in the table, for
2 x 2 systems, what is the approximate relationship between the number of iterations required for the Jacobi Method and the number of iterations required for the Gauss-Seidel Method to obtain approximately the same approximation (that is, the same degree of accuracy)? Suppose you were told that for a certain2 x 2 system of equations and given a certain initial guess, the Jacobi Method required 40 iterations to get to||error(k)|| = 0. About how many iterations would the Gauss-Seidel Method would require to get approximately the same results?
- We expect that an iterative method, such as Jacobi or Gauss-Seidel, will produce a sequence of approximations that get closer and closer to the true solution. In this problem we consider the question of whether we ever reach the true solution exactly. Use Jacobi’s Method to solve the system
 .
.Since the true solution is
x = (1, 1), let us center the viewing window around that point, by changing the minimum and maximum boundaries for bothx1 and x2 to−4 and 6 (bottom left part of the applet — be sure to press Enter after entering the new values). For this problem, use an initial guess ofx(0) = (4, −3). Also, for this problem do not write down the results of your iterations.- Do 10 iterations. On the graph in the applet, does it appear that the approximations have already reached the true solution? Now zoom in about 10 times by clicking on the Zoom in button, and answer the same question.
- Do 10 more iterations, for a total of 20, and answer the same question as in (a). As in (a), zoom in about 10 more times and answer the same question again.
- Does it appear that we will ever reach the solution exactly? Although it would be nice to have the true solution exactly, is an approximation actually good enough? (Note: if you attempt to continue to iterate and zoom in, you will eventually, perhaps quickly, exhaust the precision of your computer, and it may produce strange results — your computer can zoom in only so far.)
David M. Strong, "Iterative Methods for Solving [i]Ax[/i] = [i]b[/i] - Exercises, Part 1: Jacobi and Gauss-Seidel Methods," Convergence (July 2005)




