- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Iterative Methods for Solving Ax = b - Introduction to the Iterative Methods
One of the most important problems in mathematics is to find the values of the n unknowns x1, x2, ..., xn that satisfy the system of n equations
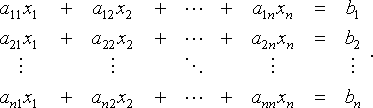
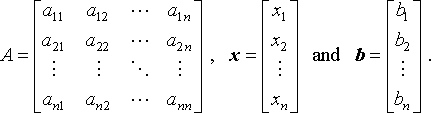

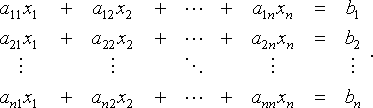
That is, we want to solve for x in
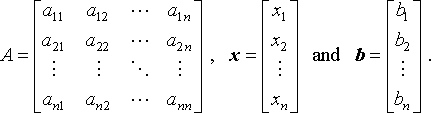
A is commonly referred to as the coefficient matrix. In order to save space, we usually write column vectors in coordinate form,
Suppose we knew the true values of
The fundamental idea of an iterative method is to use
Iterate means repeat, so an iterative method repeats this process over and over, each time using the current approximation to produce a better approximation for the true solution, until the current approximation is sufficiently close to the true solution -- or until you realize that the sequence of approximations resulting from these iterations is not converging to the true solution.
So given an initial guess or approximation ![]() x
x![]()
![]() ;
;
Since we don’t actually have the true solution x (if we did, why would we be trying to find it?), we can’t check to see how close our current approximation
Another way to check the accuracy of our current approximation is by looking at the differences in successive approximations,
This idea of iteration is not unique to linear algebra. An example that may be familiar to you is Newton’s Method , which finds approximations to the root x of

Under the right conditions, x(k) ![]() x [that is, f (xk)
x [that is, f (xk) ![]() 0] as
0] as ![]()
![]() .
.
David M. Strong, "Iterative Methods for Solving [i]Ax[/i] = [i]b[/i] - Introduction to the Iterative Methods," Convergence (July 2005)




