- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Iterative Methods for Solving Ax = b - Jacobi's Method
Perhaps the simplest iterative method for solving Ax = b is Jacobi’s Method. Note that the simplicity of this method is both good and bad: good, because it is relatively easy to understand and thus is a good first taste of iterative methods; bad, because it is not typically used in practice (although its potential usefulness has been reconsidered with the advent of parallel computing). Still, it is a good starting point for learning about more useful, but more complicated, iterative methods.
Given a current approximation
x(k) = (x1(k), x2(k), x3(k), …, xn(k))
for x, the strategy of Jacobi's Method is to use the first equation and the current values of x2(k), x3(k), …, xn(k) to find a new value x1(k+1), and similarly to find a new value xi(k) using the i th equation and the old values of the other variables. That is, given current values x(k) = (x1(k), x2(k), …, xn(k)), find new values by solving for
x(k+1) = (x1(k+1), x2(k+1), …, xn(k+1))
in
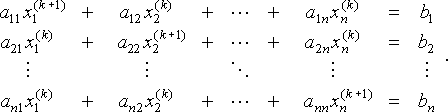
This system can also be written as

To be clear, the subscript i means that xi(k) is the i th element of vector
x(k) = (x1(k), x2(k), …, xi(k), …, xn(k) ),
and superscript k corresponds to the particular iteration (not the kth power of xi ).
If we write D, L, and U for the diagonal, strict lower triangular and strict upper triangular and parts of A, respectively,
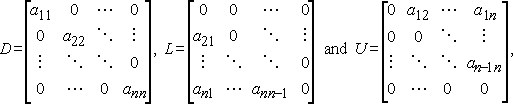
then Jacobi’s Method can be written in matrix-vector notation as
Example 1
Let's apply Jacobi's Method to the system
 .
.At each step, given the current values x1(k), x2(k), x3(k), we solve for x1(k+1), x2(k+1), and x3(k+1) in
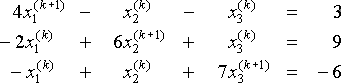 .
.So, if our initial guess x(0) = (x1(0), x2(0), x3(0)) is the zero vector 0 = (0,0,0) — a common initial guess unless we have some additional information that leads us to choose some other — then we find x(1) = (x1(1), x2(1), x3(1) ) by solving
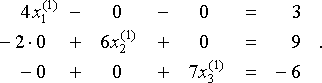
So x(1) = (x1(1), x2(1), x3(1)) = (3/4, 9/6, −6/7) ≈ (0.750, 1.500, −0.857). We iterate this process to find a sequence of increasingly better approximations x(0), x(1), x(2), … . We show the results in the table below, with all values rounded to 3 decimal places.
We are interested in the error e at each iteration between the true solution x and the approximation x(k): e(k) = x − x(k) . Obviously, we don't usually know the true solution x. However, to better understand the behavior of an iterative method, it is enlightening to use the method to solve a system Ax = b for which we do know the true solution and analyze how quickly the approximations are converging to the true solution. For this example, the true solution is x = (1, 2, −1).
The norm of a vector ||x|| tells us how big the vector is as a whole (as opposed to how large each element of the vector is). The vector norm most commonly used in linear algebra is the l2 norm:
For example, if x = (1, 2, −1), then
In this module, we will always use the l2 norm (including for matrix norms in subsequent tutorials), so that || || always signifies || ||2.
For our purposes, we observe that ||x|| will be small exactly when each of the elements x1, x2, …, xn in x = (x1, x2, …, xn ) is small. In the following table, the norm of the error becomes progressively smaller as the error in each of the three elements x1, x2, x3 becomes smaller, or in other words, as the approximations become progressively better.
| k | x(k) | x(k) − x(k-1) | e(k) = x − x(k) | ||e(k)|| | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.000 | -0.000 | -0.000 | − | − | − | -0.000 | -0.000 | -1.000 | 2.449 |
| 1 | 0.750 | 1.500 | -0.857 | -0.000 | -0.000 | -0.857 | 0.250 | 0.500 | -0.143 | 0.557 |
| 2 | 0.911 | 1.893 | -0.964 | 0.161 | 0.393 | -0.107 | 0.089 | 0.107 | -0.036 | 0.144 |
| 3 | 0.982 | 1.964 | -0.997 | 0.071 | 0.071 | -0.033 | 0.018 | 0.036 | -0.003 | 0.040 |
| 4 | 0.992 | 1.994 | -0.997 | 0.010 | 0.029 | 0.000 | 0.008 | 0.006 | -0.003 | 0.011 |
| 5 | 0.999 | 1.997 | -1.000 | 0.007 | 0.003 | -0.003 | 0.001 | 0.003 | 0.000 | 0.003 |
| 6 | 0.999 | 2.000 | -1.000 | 0.000 | 0.003 | 0.001 | 0.000 | 0.001 | 0.000 | 0.001 |
| 7 | 1.000 | 2.000 | -1.000 | 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| 8 | 1.000 | 2.000 | -1.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
For this example, we stop iterating after all three ways of measuring the current error,
x(k) − x(k-1), e(k), and ||e(k)||,
equal 0 to three decimal places. In practice, you would normally choose a single measurement of error to determine when to stop.
David M. Strong, "Iterative Methods for Solving [i]Ax[/i] = [i]b[/i] - Jacobi's Method," Convergence (July 2005)




