- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Raindrops - Modeling Large Raindrops
For large raindrops, say with diameter 0.05 inches (or 0.004 feet), a size typical of drops in a thunderstorm), the force of air resistance is better modeled as a multiple of the square of the velocity. The differential equation now has the form
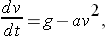
where a is another constant. In this case, the experimental evidence yields a value for a of 0.115. With the same initial condition, v(0) = 0, we have a new initial value problem. We will use Euler's Method to approximate the solution of this new problem, this time over the time interval from 0 to 2 seconds.
- What are the units for the constant a?
- Plot a slope field for the new differential equation, and confirm the reasonableness of the selected time interval. Does it look as though the solution will reach terminal velocity in 2 seconds?
- This time calculate the terminal velocity from the differential equation first, before finding a solution. Express your answer in both feet/sec and miles/hour.
- Enter in your worksheeet a general formula for vk in terms of vk - 1. Create and plot all the points (tk, vk) for k ranging from 1 to n = 100.
- Check your results by overlaying the solution plot on the slope field from Step 2.
- Estimate the terminal velocity from your computed solution, and compare the result with your calculation in Step 3.
- Compare your terminal velocity with what you obtained in Part 1 as the velocity when a raindrop hits the ground after falling 3000 feet. Which model seems more reasonable?
- As you have seen, a thunderstorm drop approaches its terminal velocity quite rapidly -- but not as rapidly as a drizzle drop. Assuming that the velocity is constant during the whole duration of the fall, estimate the time it takes the drop to fall to the ground from 3000 feet. How does this time compare to your time-of-fall answer on Page 2, where no air resistance was assumed?
David A. Smith and Lawrence C. Moore, "Raindrops - Modeling Large Raindrops," Convergence (December 2004)




