- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Three Party Elections: Interactive Examples - Introduction
Suppose that we have an election with three candidates: A, B, and C. On a standard ballot (like those used in most elections around the world) the three candidates would be listed and each voter would have to choose one. While the voter in this situation has only three choices, there are really six possible preferences that the voter can have. For example, the preference "A>B>C" means that the voter prefers A to B and B to C. In this case the voter would select "A" on the ballot. However, this voter would be unable to distinguish herself from a voter whose preference is "A>C>B."
Why does it matter that voters in these situations cannot express their full preferences? It is especially important in elections where no candidate receives a majority of the votes. For example, in the 1998 Minnesota gubernatorial election, Reform Party candidate Jesse Ventura received 37% of the votes, with the candidates from the other two parties getting 34% and 28%. Even though no candidate received a majority, Ventura received a plurality -- more votes than any other candidate -- and was declared the winner. Should Ventura have won the election? It can be argued that most of the people who did not vote for Ventura would have had him as their third choice. If that were really true, then as many as 63% of the voters had Ventura as their last-place choice. Perhaps if voters in this election had been able to express their full preference, the outcome would have been different.
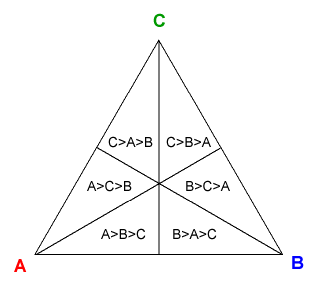
When we want to describe how many voters have each of the six possible preference orders, we use a diagram developed by Donald Saari [1] called the representation triangle. Each vertex of the triangle is labeled by a candidate, and the six regions of the triangle each represent one of the six preference orders. For example, the region labeled "A>B>C" is the region of points that are closest to A, second-closest to B, and farthest from C. A good way to remember this is that "closer is better": the regions closest to A represent the voters that have A as their top choice, and the regions second-closest to A represent the voters whose second choice is A.
Let's illustrate how the triangle works using an example from [4]. Suppose that the children in a class are trying to decide what kind of drinks they should have during lunch: soda, milk, or juice. The teacher asks the students to rank their preferences in order, and the results are as follows:
| Votes | Preference |
|---|---|
| 6 | Milk > Soda > Juice |
| 5 | Soda > Juice > Milk |
| 4 | Juice > Soda > Milk |
This voter profile would be represented by the diagram below.
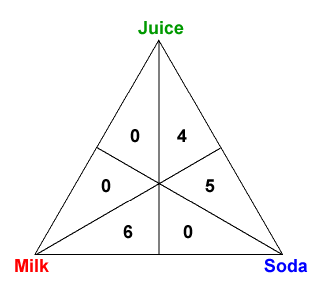
We put a zero in a region whenever the corresponding preference is held by zero voters. In this example, only 3 of the 6 possible preference orders were actually expressed by the students.
Determining the Winner
The most common method for determining the winner of an election is the one we have already discussed: the plurality method. Voters simply cast a vote for their top preference. The candidate, if any, who receives more votes than any other is the winner. In the diagram below, the plurality totals can be determined by adding up the numbers in the regions corresponding to each candidate. The red regions correspond to A, the blue regions to B, and the green regions to C.
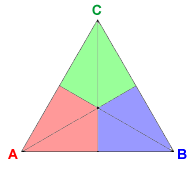
In the interactive mathlet below, you can explore the plurality method by adding and subtracting voters from each of the six regions. In all of the interactive diagrams, left-clicking adds voters and right-clicking subtracts voters.
To see one of the disadvantages of the plurality method, consider the "milk, soda, juice" example above. Milk is the plurality winner because it receives 6 votes, more than any other candidate. But while milk is top-ranked by more children than any other candidate, it is bottom-ranked by all other children. If 9 out of the 15 voters (a clear majority) ranked milk last, should it really be the winner? Perhaps we need a new way to determine the winner in situations like this.
James E. Hamblin, "Three Party Elections: Interactive Examples - Introduction," Convergence (July 2006)




