- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
CalcPlot3D, an Exploration Environment for Multivariable Calculus - Taylor Polynomials of a Function of Two Variables (1st and 2nd degree)
The way the Taylor polynomials of a function of one variable progressively converge to the graph of the function like y = cos x is really quite impressive and is inherently interesting. We can extend this topic into three dimensions using CalcPlot3D.
As an exercise, I require my students to generate the linear and quadratic Taylor polynomials of a function of two variables using the partial derivatives of the function evaluated at a particular point.
\( \begin{eqnarray} f(x,y) &\approx L(x,y) = f(a,b) &+ f_x(a,b)(x-a) + f_y(a,b)(y-b) \qquad (1^{st}\text{-deg. Taylor poly or tangent plane})\\ f(x,y) &\approx Q(x,y) = f(a,b) &+ f_x(a,b)(x-a) + f_y(a,b)(y-b) \\ &+\frac{f_{xx}(a,b)}{2}(x-a)^2 &+ f_{xy}(a,b)(x-a)(y-b) + \frac{f_{yy}(a,b)}{2}(y-b)^2 \qquad (2^{nd}\text{-deg. Taylor poly})\end{eqnarray}\)
| Exercise: | Determine the 1st and 2nd degree Taylor polynomials in two variables for the given function. Simplify both polynomials. Show all work including all partial derivatives and using the formula clearly with functional notation in the first step. Please also provide a printout of the given surface along with each of the Taylor polynomials. (That’s 2 printouts all together.) Include the point on the surface where the polynomial is tangent to the surface. Use the Format Surfaces option on the View Settings menu so that the Taylor polynomial is reverse color and transparent so it’s possible to tell the two surfaces apart. If necessary, zoom out and the rotate to a view that shows the surfaces clearly. Then use the Print Graph option on the File menu of the applet to print the graph. \(f(x,y) = \sin(2x) + \cos y\) for x,y near (0,0) |
| Answers: | 1st-degree Taylor Polynomial of f: | 2nd-degree Taylor Polynomial of f: | |
| \(L(x,y)=1+2x\) | \(Q(x,y)=1+2x-\frac{1}{2}y^2\) | ||
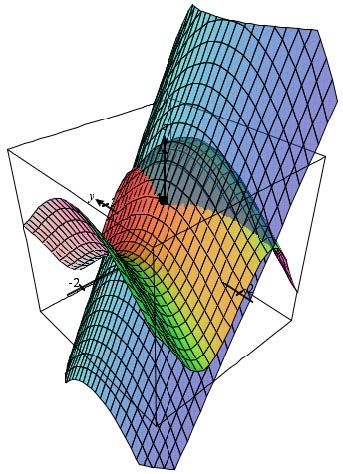 |
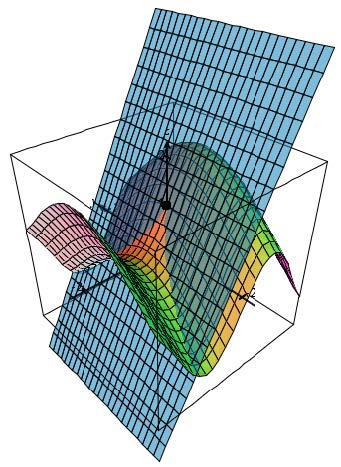 |
There is also a feature of the applet that will allow you to demonstrate higher-degree Taylor polynomials for a function of two variables.
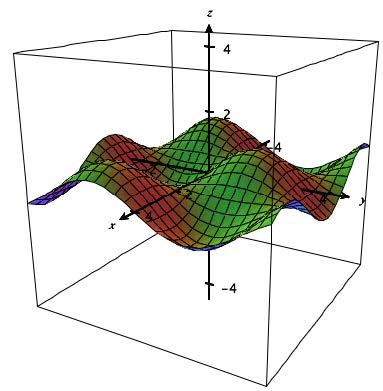 Example:
Example:
- Graph the function, \(f(x,y)=\cos(x)\sin(y)\). Then zoom out to -4 to 4 in the x and y-directions.
- Now select the View Taylor Polynomials option from the Tools menu at the top of the applet. It will take a few seconds as the computer calculates the partial derivatives and creates the Taylor polynomials. This example is successfully calculated all the way up to the 15th degree polynomial. Once it is ready, the original function is graphed as a wireframe and the 1st degree Taylor polynomial (the tangent plane) is shown. A scrollbar appears along the bottom edge of the 3D plot. Use this scrollbar to scroll through the various Taylor polynomials of this function. Note that only odd degrees add new terms for this particular function. As you increase the degree of the Taylor polynomial notice how the polynomial of two variables fits the original surface better and better around the origin until it is a fairly good approximation of the whole visible surface at the 15th degree.
- To better view the Taylor polynomial itself (shown in the text window just above the 3D plot), you can click and drag on the equation and view all terms, dragging the equation left and right. You can also use the Tools menu option
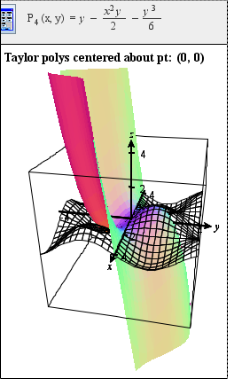 Use Factorials in Taylor Polynomials to switch this property on or off. Using factorials makes the form of the terms of the higher order Taylor polynomials easier to see, and the terms also generally take up less horizontal space each.
Use Factorials in Taylor Polynomials to switch this property on or off. Using factorials makes the form of the terms of the higher order Taylor polynomials easier to see, and the terms also generally take up less horizontal space each. - You can also vary the center point for the Taylor expansion using the Tools menu option just below View Taylor Polynomials. The default center point is the origin.
- Other nice functions to try centered about the origin include:
- \(f(x,y)=\cos(x)-\sin(y)\)
- \(f(x,y)=\sin(2x)-\cos(y)\)
- \(f(x,y)=\sin(x^2+y^2)\)
- \( f(x,y)=xe^y+1\)
- \(f(x,y)=e^{x^2+2x-y}\)
- \(f(x,y)=\arctan(xy)\)
- \(f(x,y)=\arctan(x+y)\)
Click here to open the CalcPlot3D applet in a new window.
Click here to open a pdf file which contains the instructions for the activity.
Paul Seeburger (Monroe Community College), "CalcPlot3D, an Exploration Environment for Multivariable Calculus - Taylor Polynomials of a Function of Two Variables (1st and 2nd degree)," Convergence (November 2011), DOI:10.4169/loci003781




