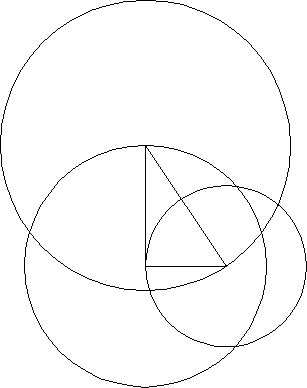- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Rethinking Pythagoras - 1. Introduction
How can we use calculus to enhance geometric understanding across multiple geometries? Here we discuss the Pythagorean Theorem and its "evil twins" in alternate geometries, ending, in the appendix, with discovery activities appropriate either for college geometry students or for accelerated calculus students wanting to use their knowledge to explore alternate geometries.
Many of the proofs of the Pythagorean Theorem begin with Figure 1a, showing a right triangle with squares constructed on each side. These proofs usually proceed by matching pieces from the smaller squares to sub-regions of the larger square. However, since squares do not exist in non-Euclidean geometries, we use circles to relate lengths of sides to areas, as in Figure 1b. In this case, if we call the lengths of sides of the triangle \(a\), \(b\), and \(c\) in ascending order of length, then it is easy to see that the circles have area \(\pi a^2\), \(\pi b^2\), and \(\pi c^2\), at least in Euclidean geometry. We note that the switch from squares to circles comes at a cost: figure 1b is both harder to interpret than 1a, and does not constitute a rigorous proof in the Euclidean case as does 1a. However, the universality of circles will make up for the messiness of the picture, and will allow us to conduct numerical explorations that lead us to conjectures in Euclidean, spherical, and hyperbolic geometries. These conjectures can be followed up with rigorous proof, and much of this article describes the "rigorization" of some of those conjectures.
In Section 2, we discuss the Pythagorean Theorem in the Euclidean plane. We move to its twin in spherical geometry in Section 3, rigorously treating circumference and area of circles on the unit sphere, then use dynamic software, together with our formula for area, to conjecture the Spherical Pythagorean Theorem. We repeat the process in the Poincaré Disc Model of hyperbolic geometry in Section 4a, and in the hyperboloid model (also known as the Minkowski-Weierstrass model) in Section 4b (both of which may be considered advanced). In all cases, we make use of the tools of calculus and offer evidence in support of our conjectures (in the way of other known calculus formulas that are implied by our answers), though we do not prove all of the conjectures. We summarize in Section 5.
In the Appendix, we give discovery activities that could be used in the classroom or as an assignment for students; in fact the author has used them at the end of a non-Euclidean Geometry course. Although they are targeted to post-calculus geometry students, the activities are gradual, and could be made accessible to students at lower levels by cutting some of the last activities from each non-Euclidean geometry, and/or cutting one or more of the non-Euclidean geometries from the activity. Indeed, the weaker students in the author's classes usually do not complete the hyperbolic elements of the discovery activity. The activities also seem appropriate as extra-credit problems for calculus students wanting to peek at more advanced material.
We use Geometry Playground [1], as the basis for our discovery activities. Although there are other packages that allow discovery in non-Euclidean geometries (Cinderella [2], Spherical Easel [3], NonEuclid [4], Geometry Explorer [5]), Geometry Playground combines all of the "standard" geometries (and a few unusual ones) in one package, and is available freely to anyone with an internet connection, allowing students to use it in a take-home activity.
We would like to thank the referees for many useful suggestions.
Daniel J. Heath (Pacific Lutheran University), "Rethinking Pythagoras - 1. Introduction," Convergence (May 2011), DOI:10.4169/loci003568