- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Rethinking Pythagoras - 4b. Stretching the Truth (Hyperboloid Model)
We define distances and circles in hyperbolic space analogously to how we did on the sphere, and assume that the reader is familiar with the Hyperboloid Model of hyperbolic geometry, in particular, that we envision it as the points on the upper half of the hyperboloid of two sheets \(-x^2-y^2+z^2=1\) , with (distance-inducing) differential \(ds=({dx}^2+{dy}^2-{dz}^2)^{-1/2}\) , and the fact that the upper half of the hyperbola \(y^2-x^2=1\) can be parametrized by hyperbolic trigonometric functions \(( \sinh t, \cosh t)\) in much the same way that the unit circle \(x^2+y^2=1\) can be parametrized by standard trigonometric functions \((\cos t, \sin t)\). For those who need a refresher, Wikipedia has a reference page for the Hyperboloid Model [16], and the Geometry Center has an archive containing descriptions and images concerning the Hyperboloid (Minkowski) Model [17].
4b.1 Using Differential Calculus
Let \(A\) and \(C\) represent the area and circumference, respectively, of a circle in the hyperbolic plane. Repeating an idea from Subsections 2.1 and 3.1, we note that \(dA/dr=C\). However, it takes a bit more thinking to find a formula for circumference of a hyperbolic circle.
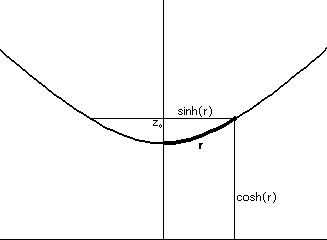
For convenience, we consider the circle with center \( (0,0,1) \). The circle then must lie inside the Euclidean plane \(z=z_0\) for some appropriate \(z_0\), so the projection of the circle onto the \(xz\)-plane looks like the horizontal segment in Figure 6 (see also Figure 7 for the three dimensional picture). This segment also represents a diameter for the Euclidean circle coinciding with the hyperbolic circle.
The radius of the (hyperbolic) circle in question is the arclength, along the hyperbola in the \(xz\)-plane, from \( (0,1) \) to \( (\sinh r,\cosh r) \), where we use the hyperbolic differential to measure length. In this case, since \(y=0\), the differential is \(ds=({dx}^2+{dz}^2)^{1/2}\), so we obtain:
hyperbolic radius \(=\int_0^r (\cosh^2(t)-{\sinh^2(t)})^{1/2} dt\)
It is easy to check that \( \cosh^2 t-\sinh^2 t=1\), so the integral in question evaluates to just \(r\). Then the radius of the hyperbolic circle is \(r\), and the same circle, considered as a Euclidean circle in the plane \(z=z_0\) (\(=\cosh r)\) has radius \(\sinh r\). Hence the circumference of either circle (hyperbolic or Euclidean) is \(C=2 \pi \sinh r\) (since in the plane \(z=z_0\), \(dz=0\), and the Euclidean and hyperbolic distances are equal). Note the resemblance to the spherical case, both in process and final answer.
Now since \(dA/dr=C\) and \(C=2 \pi \sinh r\), we obtain \(dA/dr=2 \pi \sinh r\). Antidifferentiation gives us \(A=2 \pi \cosh r+K\). Inspection of the known value of \(A\) (i.e., when \(r=0\)) gives us \(K=-2 \pi\), so that \(A=2 \pi \cosh r-2 \pi\), a remarkable resemblance to the spherical case!
It is elementary to verify that \(\frac{d}{dx} \sinh x=\cosh x\) and \(\frac{d}{dx} \cosh x=\sinh x\), so that calculating MacLaurin series for each is a straightforward matter. Then we can see that:
\(A=2 \pi \cosh r-2 \pi=2 \pi (1+\frac{1}{2!}r^2+\frac{1}{4!}r^4+\cdots )-2 \pi \approx \pi r^2\)
\(C=2 \pi \sinh r=2 \pi (\frac1{1!}r^1+\frac1{3!}r^3+\frac1{5!}r^5+\cdots )-2 \pi \approx 2\pi r\)
the latter approximations true for small \(r\). Again it is clear that both expressions are asymptotic to their Euclidean counterparts when distances are small. In addition, they imply hyperbolic trigonometric analogs for the familiar limit formulas from calculus:
\(\lim_{r \rightarrow 0}(\frac{\cosh r-1}{r^2} )=\frac{1}{2}\)
implied by the former, and
\(\lim_{r \rightarrow 0}(\frac{\sinh r}{r} )=1\)
implied by the latter. It would be difficult to determine whether your universe were Euclidean, spherical, or hyperbolic if you were trapped in only one small corner of it, since in any of the three geometries, measurements on a small scale are either Euclidean or almost Euclidean. Indeed, physicists have not yet agreed on the overall shape of our universe [18], [19], [20].
4b.2 Using Integral Calculus
We can calculate area of a hyperbolic circle by using integral calculus as well. We assume that our circle is centered at the point \((0,0,1)\), and that the circle lies in the plane \(z=z_0\), parallel to the \(xy\)-plane, as in Figure 7. Then the interior of the circle is a surface of rotation, its area given by the integral:
\(A=2 \pi \int_1^{z_0} x ([\frac{dx}{dz} ]-1)^{1/2}\)
Substituting \(x=(z^2-1)^{1/2}\) into this equation gives us a particularly simple integral, evaluating to:
(5)\(A=2 \pi(z_0-1)\)
Since we are interested in the relationship between area and radius, we now calculate the radius of the circle in terms of \(z_0\). The radius can be seen as the arclength of the curve \(x=(z^2-1)^{1/2}\) from \(z=1\) to \(z_0\), using the hyperbolic differential \(ds=(dx^2-dz^2)^{1/2}\) (since \(y=0\)) to measure distance. Then we obtain the integral:
\(r=\int_1^{z_0}([\frac{dx}{dz} ]-1)^{1/2} dz\)
Substitution gives us:
\(r=\int_1^{z_0} \frac{1}{(z^2-1)^{1/2}} dz\)
From here, we make the hyperbolic trigonometric substitution \(z=\cosh t\), \(dz=\sinh t, dt\) and simplify, obtaining:
\(r=\int_0^{\cosh^{-1}(z_0)} 1dt\)
Hence we have \(r=\cosh^{-1}(z_0)\), or in reverse, \(z_0=\cosh(r)\). Note that substitution of this value into Equation (5) gives us:
(6)\(A=2 \pi \cosh r-2 \pi\)
just as in Subsection 4b.1. From here we can differentiate to verify our formula for circumference.
4b.3 The Pythagorean Theorem
After seeing the similarities between spherical and hyperbolic area, we begin with a headstart; our initial conjecture at a Hyperbolic Pythagorean Theorem is \(\cosh a \cdot \cosh b=\cosh c\). In Geometry Playground [1], we choose hyperbolic geometry and construct a right triangle and its edge-circles as in Figure 1b, or simply open Geometry Playground with a pre-constructed hyperbolic right triangle in the Minkowski-Weierstrass Model, and then construct the edge-circles on that right triangle as in Figure 1b.
Measuring the area \(A\) of each circle, and calculating \(\cosh r=(A+2 \pi)/(2 \pi)\) from Equation (6), it shouldn't take long for the relationship \(\cosh a \cdot \cosh b=\cosh c\) to stand out, as expected. In fact, though we leave it without proof, this is the "Hyperbolic Pythagorean Theorem."
We again note that as \(a\), \(b\), and \(c\) decrease, the Hyperbolic Pythagorean Theorem approaches the Euclidean one. Substituting MacLauren series \(\cosh r=1+r^2/{2!}+r^4/{4!}+\cdots\) for \(\cosh a\), \(\cosh b\), and \(\cosh c\), we obtain:
\((1+\frac{1}{2!}a^2+\frac{1}{4!}a^4+\cdots )(1+\frac{1}{2!}b^2+\frac{1}{4!}b^4+\cdots)=1+\frac{1}{2!}c^2+\frac{1}{4!}c^4+\cdots\)
Distributing the left, we arrive at
\(1+\frac{1}{2!}a^2+\frac{1}{2!}b^2+\cdots=1+\frac{1}{2!}c^2+\cdots\)
with all remaining terms of degree 4 or higher. Since we are assuming \(a\), \(b\), and \(c\) are all small, we ignore the higher order terms. Canceling the constant terms and multiplying by \(2\), we obtain the Euclidean Pythagorean Theorem.
Daniel J. Heath (Pacific Lutheran University), "Rethinking Pythagoras - 4b. Stretching the Truth (Hyperboloid Model)," Convergence (May 2011), DOI:10.4169/loci003568