- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Interactive Supplements to Rick's Tricky Six Puzzle
The following applets on "Rick Wilson's Tricky Six puzzle" supplement the paper by Alex Fink and Richard Guy in the April 2009 issue of Mathematics Magazine. See the abstract of the article below. |
|
Click here or on the cover picture above to read the article as a pdf file. Click on any screen shot to open the corresponding applet in a new window. |
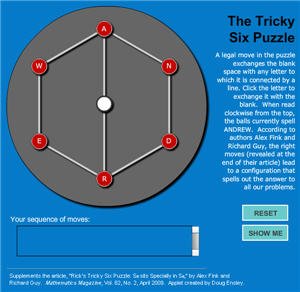
This applet illustrates the puzzle described in the last paragraph of the article. It also ties in with the cover image for this issue of Mathematics Magazine. |
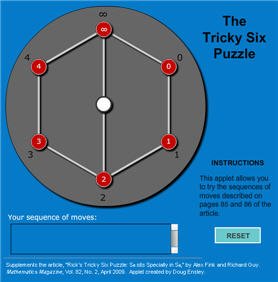
This applet allows you to practice the moves on pages 85-86 of the article. It's a good idea to practice before tackling the puzzle! |
This applet allows you to try the puzzle using the description on page 85 of the article. This is harder than you think! |
Rick’s Tricky Six Puzzle: S5 Sits Specially in S6
by Alex Fink and Richard Guy
Abstract. Rick Wilson identified a sliding block puzzle, the Tricky Six puzzle, in which a uniquely small fraction of the possible scrambled arrangements of the six moving pieces can be restored to the solved state. The permutations one can perform form the abstract group S5, the symmetric group on five letters, but surprisingly they aren't any of the "obvious" copies of S5 in S6 that fix a single point and allow the other five to be permuted arbitrarily. This special S5 comes from the outer automorphism of S6, a remarkable group-theoretic map whose presence is felt in several combinatorial objects. We track down this outer automorphism in the Tricky Six puzzle as well as the projective plane of order 4, the Hoffman-Singleton graph, the Steiner system S(5,6,12), and a couple of error-correcting codes.
Doug Ensley (Shippensburg Univ.), "Interactive Supplements to Rick's Tricky Six Puzzle," Convergence (February 2010), DOI:10.4169/loci003295