- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Japanese Theorem for Nonconvex Polygons - First Generalizations
First Generalizations
Just after the turn of the twentieth century the Japanese mathematician Yoshio Mikami heard of a theorem from a friend, who had heard it from someone from China. No proof accompanied the theorem. In 1905 Mikami stated and proved the theorem ([Mi]):
If in a polygon inscribed in a circle all possible diagonals that can be drawn from a vertex are drawn and the successive triangles thus formed are inscribed with circles, then their radii will be together equal for any of the vertices.
For example, the polygon in Figure 2 is triangulated with diagonals meeting at two different vertices, but the sums of the radii are equal.
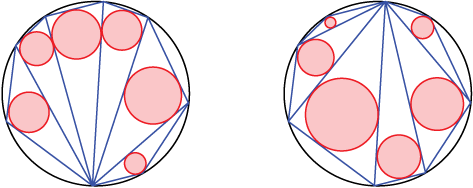 Figure 2
Figure 2
This remarkable theorem immediately got the attention of other Japanese mathematicians and new proofs appeared in print the following year—one in [Gr] and five compiled in [Hay]. In this latter paper, the author points out that this "soi-disant théorème Chinois" (so-called Chinese theorem) is simply a generalization of Maruyama's hundred-year-old sangaku problem and could be established from it using induction. Moreover, Fujita's books were commonly used in schools, so he contends that the theorem's Chinese origin is "douleuse" (doubtful).
This theorem received its widest exposure when it appeared in Roger Johnson's 1929 classic text Modern Geometry ([p. 193, Jo1]), which was reprinted by Dover in 1960 as Advanced Euclidean Geometry ([Jo2]).
In 1985 Ross Honsberger observed that there are many other ways to triangulate an \(n\)-gon with nonintersecting diagonals (the number of ways is precisely the \( (n-2)\)nd Catalan number) and that invariance holds in these situations as well ([p. 24, Ho]):
A great deal more might have been claimed [by Johnson], for this same sum results for every [author's emphasis] way of triangulating the polygon!
 Figure 3
Figure 3
We call this the Japanese theorem for polygons.
David Richeson, "The Japanese Theorem for Nonconvex Polygons - First Generalizations," Convergence (December 2013)




