Mathematics Magazine - April 2017

Mathematics is often surprising and has the ability to elucidate what seem to be unfathomable facts. Prince Rupert won a wager for showing that a cube could pass through another cube of the same size. An article in this issue shows that the dodecahedron and the icosahedron share Rupert’s property. Other articles consider writing rational numbers as decimals from right to left, the bounce-back ability of Weebles and other roly poly toys, how look-up tables can be constructed to solve the Lights Out puzzle, and using polyominoes to count multiplex defects for digital cameras.

This issue also has the problems and solutions to the 77th Annual William Lowell Putnam Exam. Other articles, proofs without words, Problems, and Reviews complete the issue.

—Michael A. Jones, Editor

JOURNAL SUBSCRIBERS AND MAA MEMBERS:

To read the full articles, please log in to the member portal by clicking on 'Login' in the upper right corner. Once logged in, click on 'My Profile' in the upper right corner.

Vol. 90, No. 2, pp. 85 – 164

Articles

Platonic Passages

p. 87.

Richard P. Jerrard, John E. Wetzel, and Liping Yuan

It is well known that a hole can be cut in a cube large enough to permit a second cube of equal size to pass through, a result attributed to Prince Rupert of the Rhine by J. Wallis more than three centuries ago. C. Scriba showed nearly 50 years ago that the tetrahedron and the octahedron have this same property. Somewhat surprisingly, the remaining two platonic solids, the dodecahedron and the icosahedron, also have this property: each can be passed through a suitable tunnel in another of the same size and kind. We supply the details.

To purchase from JSTOR: 10.4169/math.mag.90.2.87

Weebles Only Wobble But Eggs Fall Down

p. 99.

Subhranil De

Why does a roly-poly toy tend to stand upright on its less pointed end while an egg does not? The answer lies in a simple principle that governs the nature of the mechanical equilibrium of a solid of revolution. A roly-poly toy is at a stable equilibrium on its vertex while an egg is at an unstable equilibrium. The roly-poly toy’s center of mass is vertically below the center of curvature of its vertex, while for the egg it is the other way around. Although this simple but powerful principle is known, in this article we present a contrasting analysis that not only verifies this principle, but also provides the answer to another interesting question: Is there another simple principle that governs the nature of the equilibrium in the critical situation where the center of curvature of the vertex happens to coincide with the center of mass?

To purchase from JSTOR: 10.4169/math.mag.90.2.99

An Alternate Method to Compute the Decimal Expansion of Rational Numbers

p. 108.

Amitabha Tripathi

Rational numbers, except those with denominators of the form 2^a5^b, have a recurring decimal expansion. It is usual to write these digits from left to right. We give a procedure to write the decimal digits from the opposite end—right to left.

To purchase from JSTOR: 10.4169/math.mag.90.2.108

Capelli-Rédei Theorem, Solvable Quintics, and Finite Fields

p. 114.

Matt D. Lunsford

A situation analogous to the classic casus irreducibilis exists in the context of irreducible cubic polynomials over finite fields if it is required that solvability by radicals means solvability by irreducible radicals. In this paper we extend this analogy to irreducible quintics over finite fields by use of the Capelli–Rédei theorem.

To purchase from JSTOR: 10.4169/math.mag.90.2.114

Proof Without Words: Partial Column Sums in Pascal's Triangle

p. 117.

Ángel Plaza

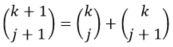
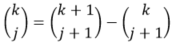
Based on the binomial property , written as , the sum of consecutive column entries of Pascal’s triangle is written as a difference of two binomial coefficients in the next column, which generalizes the so-called hockey stick identities.

To purchase from JSTOR: 10.4169/math.mag.90.2.117

The Asymptotic Behavior of the Binomial Coefficients

p. 119.

Paul Levrie

In this note we give a rigorous proof by elementary means of the asymptotic behavior of the binomial coefficients. As an application we look at the convergence of the binomial series at the endpoints of the convergence interval.

To purchase from JSTOR: 10.4169/math.mag.90.2.119

Proof Without Words: A Recursion for Triangular Numbers and More

p. 124.

Tom Edgar

We visually demonstrate a recurrence satisfied by the triangular numbers and hence all quadratic sequences including all types of polygonal numbers.

To purchase from JSTOR: 10.4169/math.mag.90.2.124

Chasing the Lights in Lights Out

p. 126.

C. David Leach

Lights Out is a game played on a grid of light-up buttons. At the start of the game, the lights are lit in a seemingly random configuration. A button changes states whenever it or one of its neighbors is pressed. The goal is to turn all of the lights out. Light chasing is a simple strategy for winning Lights Out by using a lookup table. In this article we examine how to construct these lookup tables for several variations of the game.

To purchase from JSTOR: 10.4169/math.mag.90.2.126

Proof Without Words: Diophantus of Alexandria's Sum of Squares Identity

p. 134.

Roger B. Nelsen

We wordlessly prove (a² + b²)(c² + d²) = (ac + db)² + (ad ∓ bc)² using the Pythagorean theorem.

To purchase from JSTOR: 10.4169/math.mag.90.2.134

On Polyominoes and Digital Cameras

p. 135.

Daniel J. Heath and R. Robert Rydberg, III

We give an example of how mathematics is used in engineering by discussing whether a high resolution CMOS imager, used in digital cameras, can be manufactured according to a client’s specifications. We relate defects in a rectangular array of pixels to polyominos in order to count how many multipixel, or adjacent, defects are expected for a given number of single-pixel, or isolated, defects in a pixel array. This is done to quantify the expected number of multipixel defects in a given pixel array.

To purchase from JSTOR: 10.4169/math.mag.90.2.135

A Morley-Like Congruence Arising From Morley's Congruence

p. 142.

Romeo Meštrović

In this note, we prove a congruence by applying the famous Morley congruence to a simple binomial identity.

To purchase from JSTOR: 10.4169/math.mag.90.2.142

Problems and Solutions

p. 144.

Proposals, 2016-2020

Quickies, 1069-1070

Solutions, 1986-1990

Answers, 1069-1070

To purchase from JSTOR: 10.4169/math.mag.90.2.144

When a Sum of Powers Equals a Power

p. 150.

Adrian Chun Pong Chu

To purchase from JSTOR: 10.4169/math.mag.90.2.150

Reviews

p. 151.

Big data, the calculus of happiness, mathematics achievements of 2016, the utility of recreational mathematics

To purchase from JSTOR: 10.4169/math.mag.90.2.151

News and Letters

p. 153.

77th Annual William Lowell Putnam Mathematical Competition

To purchase from JSTOR: 10.4169/math.mag.90.2.153