- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematics Magazine - October 2008
ARTICLES
Consecutive Integers with Equally Many Principle Divisors
Roger B. Eggleton and James A. MacDougall
Every integer larger than 1 is uniquely a product of powers of primes, and we will let Pn denote the set of integers with exactly n distinct prime divisors. For example, P1 is the set of prime powers, and P3 = {30, 42, 60, 66, 70, 78, ... }. In this article we study runs of consecutive integers within any of the sets Pn. The sequence {2, 3, 4, 5} is a run of length 4 in P1, and easily seen to be the longest possible. We easily found a run of length 8 in P2 – the integers in {141, 142, ..., 148} all have exactly 2 distinct prime divisors. and our main result in the paper is the proof that the maximum possible length of a run in P2 is 10. We also derive an upper bound for the length of a run in Pn for any n. Additionally we have tabulated much interesting data about these consecutive runs for n > 2, including the first run of length 2 as far as n = 7. The longest run we discovered is in P3 and has 16 numbers beginning at 127890362. We conjecture that there is a run of length at least 2 for every n and give a procedure for constructing some such examples.
The Shot Made Round (Across) The Table (Maybe)
John H. Riley, Jr
Suppose you are shooting a billiard ball on elliptical table (with no pockets). In what ways is it possible to make your shot return to its starting point? For example, is it possible to specify the number of times the ball must hit the edge before returning to its starting point? We show that the answers to these and other questions depend first on whether the path of the ball must go around or between the foci and second on the shape (eccentricity) of the ellipse. All of this serves to illustrate the subtlety of dynamical systems.
Probabilistic Reasoning is not Logical
Ruma Falk
Most students are pretty well versed in the ground rules of logical deduction. The question is whether probabilistic inferences – which are ubiquitous in daily and scientific contexts – behave similarly. Occurrence of an event might probabilistically support another given uncertain event, namely, enhance its chances, or probabilistically confirm the event in question, that is, render it highly probable. Six basic rules of logical and probabilistic inferences of the two types are compared with each other. It turns out that probabilistic inferences are sometimes subject to the same rules as logical involvement and some other times they diverge from them. Though applying the logical rules to inferences under uncertainty may often be heuristically expedient, it is wrong in principle and it may incur faulty conclusions in important situations. Increased sensitivity to such possibilities should caution students, educators, and researchers against perfunctorily applying the habitual syllogistic rules to reasoning under uncertainty.
Wazir Circuits on an Obstructed Chessboard
Irl Bivens, Ben Klein, and Arthur Holshouser
SUMMARY: A ‘wazir’ is a now obsolete chess piece that moves exactly one square at a time vertically or horizontally. (It is sometimes referred to as a ‘single-step rook’.) In this paper we discuss an interesting parity result for wazir circuits on chess boards of arbitrary size. We allow our chess boards to be ‘obstructed’ in the sense that movement into certain squares may be forbidden. Any unobstructed square will be called ‘open’. A ‘wazir circuit’ is a sequence of moves in which the wazir begins in an open square, ends in the same square, and visits every other open square on the board exactly once. The principal result of this paper determines the parity of the number of moves the wazir makes in a specified direction (e.g. to the right) during a circuit.
NOTE
What if Archimedes Had Met Taylor?
Jason Slowbe
Archimedes developed an algorithm using inscribed and circumscribed polygons to create intervals known to converge to pi, but this algorithm does not produce a single numeric approximation of pi. Using Taylor Series and some calculus-based reasoning, we improve this algorithm to more efficiently produce numerical approximations of pi. Inspired by Archimedes, we analyze error in the area and perimeter models to make additional improvements that approximate pi even more efficiently.
Universality in Mathematical Modeling: A Comment on "Surprising Dynamics From a Simple Model"
Hideyuki Suzuki
This note is a comment on the article by Walsh in the December 2006 issue of Mathematics Magazine, which introduces two simple models that exhibit rich nonlinear dynamics. In this note, we introduce a few simple models in the fields of neuroscience and high voltage engineering. Surprisingly, the mathematical expressions for these models are identical or similar to those in the article by Walsh, though they were proposed independently. This surprising coincidence can be considered as a good example illustrating the universality of mathematical modeling.
An Elementary Proof of the Error Estimates in Simpson’s Rule
D. D. Hai and R. C. Smith
Calculus books usually give error estimates for the Trapezoidal Rule and Simpson’s Rule. The estimates, especially the error estimate for Simpson’s Rule, are somewhat mysterious, and proofs are generally considered beyond the scope of the text. We give a simple proof of the standard estimate for Simpson’s Rule based on integration by parts and give some other estimates not found in calculus books.
The Class of Heron Triangles
Raymond A. Beauregard
A Heron triangle is one with rational sides and rational area. We show that every Heron triangle is similar to one with sides 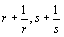 and
and 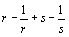 for rational numbers r and s greater than one.
for rational numbers r and s greater than one.
PROOF WITHOUT WORDS
Tangent of the Sum
Sidney H. Kung
The tangent of the sum formula is proved by using an inscribed quadrilateral whose longest side is the diameter of the circle, and the diagonals are perpendicular to the pair of oposite sides, respectively.
Fibonacci Tiles
Richard L. Ollerton
Rectangles with Fibonacci dimensions are partitioned to demonstrate several Fibonacci identities.




