- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Research Sampler 9: Key Aspects of Knowing and Learning the Concept of Function
by Marilyn Carlson and Michael Oehrtman
Why is the function concept so important?
Why is the function concept so difficult for students to understand?
Dynamic conceptualizations needed for precalculus and calculus
The process view of functions - A more formal examination
Fostering a process view of functions
Building on the process view of function: Applying covariational reasoning
Engaging covariational reasoning through analysis of function situations
Concluding remarks
References
The concept of function is central to undergraduate mathematics, foundational to modern mathematics, and essential in related areas of the sciences. A strong understanding of the function concept is also essential for any student hoping to understand calculus - a critical course for the development of future scientists, engineers, and mathematicians.
Since 1883, there have been repeated calls for school curricula to place greater emphasis on functions (College Entrance Examination Board, 1959; Hamley, 1934; Hedrick, 1922; Klein, 1883; National Council of Teachers of Mathematics, 1934, 1989, 2000). Despite these and other calls, students continue to emerge from high school and freshman college courses with a weak understanding of this important concept (Carlson, 1998; Carlson, Jacobs, Coe, Larsen & Hsu, 2002; Cooney & Wilson, 1996; Monk, 1992; Monk & Nemirovsky, 1994; Thompson, 1994a).
This article provides an overview of what is involved in knowing and learning the function concept. We have included discussions of the reasoning abilities involved in understanding and using functions, including the dynamic conceptualizations needed for understanding major concepts of calculus. Our discussion also provides information about the common conceptual obstacles that have been observed in students. We make frequent use of examples to illustrate the 'ways of thinking' and major understandings that research suggests are essential for students' effective use of functions during problem solving; and that are needed for students' continued mathematics learning.
Why is the function concept so important?
Studies have revealed that learning the function concept is complex, with many high performing undergraduates (e.g., students receiving course grades of A in calculus) possessing weak function understandings (Breidenbach, Dubinsky, Hawks, & Nichols, 1992; Carlson, 1998; Thompson, 1994a). We are beginning to understand that the conceptions and reasoning patterns needed for a strong and flexible understanding of functions are more complex than what is typically assumed by designers of curriculum and instruction (Breidenbach et al., 1992; Carlson, 1998; Thompson, 1994a). Students who think about functions only in terms of symbolic manipulations and procedural techniques are unable to comprehend a more general mapping of a set of input values to a set of output values; they also lack the conceptual structures for modeling function relationships in which the function value (output variable) changes continuously in tandem with continuous changes in the input variable (Carlson, 1998; Monk & Nemirovsky, 1994; Thompson, 1994a). These reasoning abilities have been shown to be essential for representing and interpreting the changing nature of a wide array of function situations (Carlson, Jacobs, Coe, Larsen, & Hsu, 2002; Thompson, 1994a); they are also foundational for understanding major concepts in advanced mathematics (Carlson, Smith, & Persson, 2003; Cottrill, Dubinsky, Nichols, Schwingendorf, Thomas, & Vidakovic, 1996; Kaput, 1992; Rasmussen, 2000; Thompson, 1994a; Zandieh, 2000).
It is noteworthy that many of the reform calculus texts of the early 90's, e.g., Ostabee-Zorn (1997), Harvard Calculus (Hughes-Hallett & Gleason, 1994), and C4L ( Dubinsky, Schwingendorf, & Mathews, 1994), included a stronger conceptual orientation to learning functions. Such past curriculum development projects and the educational research literature are pointing the way for future curricular interventions to assist students in developing a robust function conception - a conception that includes a view of function as an entity that accepts input and produces output and enables reasoning about dynamic mathematical content and scientific contexts. Research suggests that the predominant approach to calculus instruction is not achieving the foundational understandings and problem solving behaviors that are needed for students' continued mathematical development and course taking. It is our view that the mathematics community is ready for a careful rethinking of the precalculus and calculus curriculum - one that is driven by past work of mathematicians, as well as the broad body of research on knowing and learning function and major concepts of calculus. It is also our view that if algebraic and procedural methods were more connected to conceptual learning, students would be better equipped to apply their algebraic techniques appropriately in solving novel problems and tasks.
Why is the function concept so difficult for students to understand?
As students move through their school and undergraduate mathematics curricula, they are frequently asked to manipulate algebraic equations and compute answers to specific types of questions. This strong procedural emphasis has not been effective for building foundational function conceptions - ones that allow for meaningful interpretation and use of function in various representational and novel settings. Even understanding functions in terms of input and output can be a major challenge for most students. For example,
It is also common for developing students to have difficulty distinguishing between an algebraically defined function and an equation (Carlson, 1998). This is not surprising if one considers the various uses of the equal sign and the fact that many instructors refer to a formula as an equation. For the student, this ambiguous use of the word equation appears to cause difficulty for them in distinguishing between the use of the equal sign as a means of defining a relationship between two varying quantities, and a statement of equality of two expressions. Our recent work has shown that students benefit from explicit effort to help them distinguish between functions and equations. We have developed instructional interventions that promote students' thinking about an equation as a means of equating the output values of two functions, and the act of solving an equation as finding the input value(s) where the output values of these functions are equal.
Many students also tend to believe that all functions should be definable by a single algebraic formula. This focus often hinders flexible thinking about function situations and can lead to erroneous conclusions such as thinking that all functions must always behave "nicely" in some sense (Breidenbach et al., 1992). For example, many students tend to argue that a piecewise defined function like
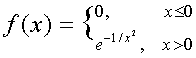 |
is actually two separate functions or that a function such as Dirichlet's example,
|
|
is not even a function at all because it "behaves badly." Similarly, many students have difficulty conceiving of different formulas representing the same function, as in the examples
|
|
and |
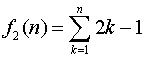 |
which define the same function on the natural numbers, albeit through very different algebraic operations. Many students also tend to assume that functions are linear or quadratic in cases where this assumption is unwarranted, expecting for example, that any "u-shaped" graph is a parabola (Schwarz & Hershkowitz, 1999). These confusions are perhaps not so surprising since functions are typically introduced in the school curriculum through specific function types, often linear or quadratic. Under such circumstances, a working definition in which functions are equated with formulas may seem perfectly reasonable to students, and even mirrors the historical understanding of mathematicians like Euler, Bernoulli, Lagrange, and d'Alembert (Kleiner, 1989; Sierpinska, 1992). It is not, however, the view that the Euler himself, and subsequently the mathematics community in general, ultimately found to be most useful. We recommend that early function curriculum and instruction include more opportunities for students to experience diverse function types emphasizing multiple representations of the same functions. This would promote a more flexible and robust view of functions - one that does not lead to inadvertently equating functions and formulas.
Another common difficulty for students is distinguishing between visual attributes of a physical situation and similar attributes of the graph of a function that models the situation. Throughout the secondary school curriculum, we teach students to attend to increasingly subtle features of graphical representations of functions, ranging from extrema and monotonicity to concavity, inflection points, and curvature. When dealing with functions modeling concrete situations, there are often similar topographical structures within the real-world setting itself (e.g., the curves of a racetrack, the elevation of a road traveling across hilly terrain, or the shape of a container being filled with liquid). The considerable salience of these physical features often creates confusion, even for students with a strong understanding of function. Several types of errors can be traced to conflating the shape of a graph with visual attributes of the situation (Carlson, 1998; Monk, 1992; Monk & Nemirovsky, 1994). Consider the following problem:
| The following diagram is the side-view of an individual cycling up and over a hill. Draw a graph of speed vs. position along the path. |
 |
| Figure 1. Students often confuse physical features of the context with the graph of a function. |
In response to this problem, many students tend to directly copy features of the diagram into their graph ( Monk, 1992). Correct interpretation of the situation is a conceptually nontrivial task. A student must ignore the fact that the picture looks like a graph, think of how riding uphill (for example) affects the speed of the cyclist, then while ignoring the shape of the hill in the picture determine how to represent the result graphically.
When interpreting graphs such as the ones in Figure 2, students often confuse velocity for position (Monk, 1992) since the curves are laid out spatially, and position refers to a spatial property. This confusion leads to erroneous claims such as: the two cars collide at
 |
| Figure 2. Students often confuse position and velocity. |
In both these examples, students are thinking of the graph of a function as a picture of a physical situation rather than as a mapping from a set of input values to a set of output values. Developing an understanding of function in such real-world situations that model dynamic change is an important bridge for success in advanced mathematics.
Students' procedural orientations to functions have also been observed in their inability to accurately express function relationships using function notation. When asked to express s as a function of t, many high performing precalculus students did not know that their objective was to write a formula in the form of "
Dynamic conceptualizations needed for precalculus and calculus
In our work to develop and validate the Precalculus Concept Assessment Instrument1 (Carlson, Oehrtman, & Engelke, submitted), we found that students' ability to respond correctly to a diverse set of function-focused tasks is tightly linked to two types of dynamic reasoning abilities. First, as mentioned above, students must develop an understanding of functions as general processes that accept input and produce output. Second, they must be able to attend to the changing value of output and rate of change as the independent variable is varied through an interval in the domain.
Understanding limits and continuity requires one to make judgments about the value of a function on intervals of infinitely many different (small) sizes. Conceptualizations based on "holes," "poles," and "jumps" as gestalt topographical features (corresponding to removable discontinuity, vertical asymptotes, and jump or one-sided discontinuity, respectively) can lead to misconceptions in more complex limiting situations, such as the definitions of the derivative and definite integral. For example, students often develop some intuitive understanding of the Fundamental Theorem of Calculus with which they can explain that the derivative of the volume of a sphere,
|
|
is its surface area; however, most of these students cannot explain why the same is not true for the volume of a cube,
To understand the relationship between average and instantaneous rates and the graphical analog between secant and tangent lines, a student must first conceive of an image as in Figure 3a, below (Monk, 1987). By employing covariational reasoning (e.g., coordinating an image of two varying quantities and attending to how they change in relation to each other), the student is able to transform the image and reason about values of various parameters as the configuration changes. Being able to answer questions that require such variation as "When point Q moves toward P, does the slope of S increase or decrease?" is significantly more difficult than being able to answer questions about the value of a function at a single point.
 |
| Figure 3. Foundational images for the definitions of a) the derivative and b) the definite integral |
Analyzing the changing nature of an instantaneous rate also requires the ability to conceive of functional situations dynamically. Consider the following question based on a classic related rates problem in calculus:
| From a vertical position against a wall, the bottom of a ladder is pulled away at a constant rate. Describe the speed of the top of the ladder as it slides down the wall. |
Reasoning about this situation conceptually is difficult for calculus students even when they are given a physical model and scaffolding questions (Monk, 1992) and is similarly challenging for beginning graduate students in mathematics (Carlson, 1999). The standard calculus curriculum presents accumulation in terms of methods of determining static quantities such as the area of an irregular region of the plane or the total distance traveled given a changing velocity (but as a completed motion). Equally important, however, is a dynamic view in which an accumulated total is changing through continual accruals (Kaput, 1994; Thompson, 1994). For example, in a typical "area so far" function as in Figure 3b, this involves being able to mentally imagine the point p moving to the right by adding slices of area at a rate proportional to the height of the graph. This requires students to engage in covariational reasoning (Carlson, Smith, & Persson, 2003) and is significantly more difficult for students than evaluating and even comparing areas at given points (Monk, 1987).
In interviews with over 40 precalculus level students, we found that students who consistently verbalized a view of function as an entity that accepts input and produces output were able to reason effectively through a variety of function-related tasks. For example, these students, when asked to find the composition of f with g, ![]() g
g![]() g
g
According to several studies, calculus students are slow to develop an ability to interpret varying rates of change over intervals of a function's domain. (Carlson, 1998; Kaput, 1992; Monk, 1992; Monk & Nemirovsky, 1994; Nemirovsky, 1996; Tall, 1992; Thompson, 1994a). According to Thompson (1994a), once students are adept at imagining expressions being evaluated continually as they "run rapidly" over a continuum, the groundwork has been laid for them to reflect on a set of possible inputs in relation to the set of corresponding outputs (p. 27). Such a covariation view of function has also been found to be essential for understanding central concepts of calculus (Cottrill et al., 1996; Kaput, 1992; Thompson, 1994b; Zandieh, 2000) and for reasoning about average and instantaneous rates of change, concavity, inflection points, and their real-world interpretations (Carlson, 1998; Monk, 1992).
The following section provides additional elaboration of these essential process and covariational understandings of functions.
The process view of functions - A more formal examination
According to Dubinsky & Harel (1992),
| An action conception of function would involve the ability to plug numbers into an algebraic expression and calculate. It is a static conception in that the subject will tend to think about it one step at a time (e.g., one evaluation of an expression). A student whose function conception is limited to actions might be able to form the composition of two functions, defined by algebraic expressions, by replacing each occurrence of the variable in one expression by the other expression and then simplifying; however, the students would probably be unable to compose two functions that are defined by tables or graphs. |
Students whose understanding is limited to an action view of function experience several difficulties. For example, an inability to interpret functions more broadly than by the computations involved in a specific formula results in misconceptions such as believing that a piecewise function is actually several distinct functions, or that different algorithms must produce different functions. More importantly, reasoning dynamically is difficult because it requires one to be able to disregard specific computations and to be able to imagine running through several input-output pairs simultaneously. This ability is not possible with an action view in which each individual computation must be explicitly performed or imagined. Furthermore, from an action view, input and output are not conceived except as a result of values considered one at a time, so the student cannot reason about a function acting on entire intervals. Thus, not only is the complex reasoning required for calculus out of reach for these students, but even simple tasks like conceiving of domain and range as entire sets of inputs and outputs is difficult.
Without a generalized view of inputs and outputs, students cannot think of a function as a process that may be reversed (to obtain the inverse of a function) but are limited to understanding only the related procedural tasks such as switching x and y and solving for y or reflecting the graph of f across the line
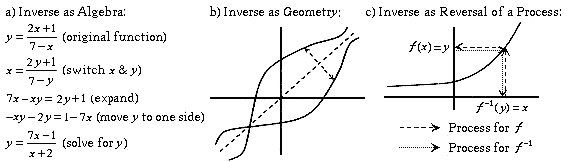 |
| Figure 4. Various conceptions of the inverse of a function. a) as an algebra problem, b) as a geometry problem, and c) as the reversal of a process. The first two of these are common among students but, in isolation, do not facilitate flexible and powerful reasoning about functional situations. |
Students who possess only the procedural orientations of Figures 4a and b, absent of the understanding of why the procedures work, will likely be unable to recognize even simple situations in which these procedures should be applied. Curriculum and instruction have not been broadly effective in building these connections in students' understanding. A recent study of over 2000 precalculus students at the end of the semester (Carlson, Oehrtman, & Engelke, submitted) showed that only
In contrast to the conceptual limitations of an action view, Dubinsky and Harel (1992) state that,
|
A process conception of function involves a dynamic transformation of quantities according to some repeatable means that, given the same original quantity, will always produce the same transformed quantity. The subject is able to think about the transformation as a complete activity beginning with objects of some kind, doing something to these objects, and obtaining new objects as a result of what was done. When the subject has a process conception, he or she will be able, for example, to combine it with other processes, or even reverse it. Notions such as |
With such a process view, students are freed from having to imagine each individual operation for an algebraically defined function. For example, given the function on the real numbers defined by
Table 1. Action and process views of functions
| Action View | Process View |
|---|---|
| A function is tied to a specific rule, formula, or computation and requires the completion of specific computations and/or steps. | A function is a generalized input-output process that defines a mapping of a set of input values to a set of output values. |
| A student must perform or imagine each action. | A student can imagine the entire process without having to perform each action. |
| The "answer" depends on the formula. | The process is independent of the formula. |
| A student can only imagine a single value at a time as input or output (e.g., x stands for a specific number). | A student can imagine all input at once or "run through" a continuum of inputs. A function is a transformation of entire spaces. |
| Composition is substituting a formula or expression for x. | Composition is a coordination of two input-output processes; input is processed by one function and its output is processed by a second function. |
|
Inverse is about algebra (switch y and x then solve) or geometry (reflect across |
Inverse is the reversal of a process that defines a mapping from a set of output values to a set of input values. |
| Domain and range are conceived at most as an algebra problem (e.g., the denominator cannot be zero, and the radicand cannot be negative). | Domain and range are produced by operating and reflecting on the set of all possible inputs and outputs. |
| Functions are conceived as static. | Functions are conceived as dynamic. |
| A function's graph is a geometric figure | A function's graph defines a specific mapping of a set of input values to a set of output values. |
Understanding even the basic idea of equality of two functions requires a generalization of the input-output process, the ability to imagine the pairing of inputs to unique outputs without having to perform or even consider the means by which this is done. Students may then come to understand that any means of defining the same relation is the same function. That is, a function is not tied to specific computations or rules that define how to determine the output from a given input. For example, the rules
 |
vs. |
 |
both provide the same results on the natural numbers and thus define the same function.
Students with a process view are also better able to understand aspects of functions such as composition and inverses. They are consistently able to correctly answer conceptual and computational questions about composition in a variety of representations by coordinating output of one process as the input for a second process. Similarly, students conceiving of inverses as reversing a process so that the old outputs become the new inputs and vice-versa (Figure 4c), or by asking "What does one have to do to get back to the original values?" were able to correctly answer a wide variety of questions about inverse functions (Carlson et al., submitted).
A process view of function is crucial to understanding the main conceptual strands of calculus (Breidenbach et al., 1992; Monk, 1987; Thompson, 1994a ). For example, the ability to coordinate function inputs and outputs dynamically is an essential reasoning ability for limits, derivatives, and definite integrals. In order to understand the definition of a limit, a student must coordinate an entire interval of output values, imagine reversing the function process, and determine the corresponding region of input values. The action of a function on these values must be considered simultaneously since another process (one of reducing the size of the neighborhood in the range) must be applied while coordinating the results. Unfortunately, most pre-calculus students do not develop beyond an action view, and even strong calculus students have a poorly developed process view that often leads only to computational proficiency (Carlson, 1998). With intentional instruction, however, students can develop a more robust process view of function (Carlson et al., submitted; Dubinsky, 1991; Sfard, 1991).
Certainly not every aspect of an action view of functions is detrimental to students' understanding, just as the acquisition of a process view does not ensure success with all functional reasoning. However, a process view of functions is crucial to developing rich conceptual understandings of the content in an introductory calculus course. The promotion of the more general 'ways of thinking' that we have advocated should result in producing curricula that are more effective for promoting conceptual structures for students' continued mathematical development.
Fostering a process view of functions
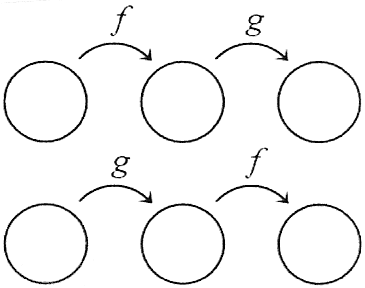 |
|
Figure 5. Which diagram represents |
Working out both the correct diagram and the correct formula for the inverse encourages students to think in terms of a general input-output process. As another example, students typically learn to carry out rote procedures when asked to solve equations such as
Ask about the action of functions on entire intervals in addition to single points. Focusing on the image of a function applied to an infinite set also encourages students to think in terms of a general process. Students should be asked to coordinate such judgments with basic compositions and inverses, asking, for example, for the length of an interval after being transformed by two linear functions. Similarly, ask students to find preimages of intervals as in the definition of limit or continuity and to reverse the process of a function even if it is not invertible (e.g., find the preimages of 1 under
Ask students to make and compare judgments about functions across multiple representations. Such questions should include multiple algebraic representations to reinforce the independence from a formula as well as the standard representations of graphs, tables, and verbal descriptions. Students should make such determinations; then compare the results for consistency, justifying or discovering why they are the same. For example, asking how the various techniques of inverting a function are related reinforces seeing a reflection across the line
Building on the process view of function: Applying covariational reasoning
The Covariation Framework
Table 2. Mental Actions of the Covariation Framework
| Mental Action | Description of Mental Action | Behaviors |
|---|---|---|
|
Mental Action 1 |
Coordinating the dependence of one variable on another variable |
|
|
Mental Action 2 |
Coordinating the direction of change of one variable with changes in the other variable |
|
|
Mental Action 3 |
Coordinating the amount of change of one variable with changes in the other variable |
|
|
Mental Action 4 |
Coordinating the average rate-of-change of the function with uniform increments of change in the input variable |
|
|
Mental Action 5 |
Coordinating the instantaneous rate-of-change of the function with continuous changes in the independent variable for the entire domain of the function |
|
In our work to study and promote students' emerging covariational reasoning abilities, we have found that the ability to move flexibly between mental actions 3, 4 and 5 is not trivial for students. We have also observed that many precalculus level students only employ Mental Action 1 and Mental Action 2 when asked to construct the graph of a dynamic function situation.
When prompting students to construct the graph of the height as a function of the amount of water in a bottle (Figure 6), we found that many precalculus students appropriately labeled the axes (MA1) and then constructed an increasing straight line (MA2). When prompted to explain their reasoning, they frequently indicated that "as more water is put into the bottle, the height of the water rises (MA2)." These students were clearly not attending to the amount of change of the height of the water level or the rate at which the water was rising.
| Imagine this bottle filling with water. Sketch a graph of the height as a function of the amount of water that's in the bottle. |
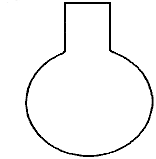 |
| Figure 6. The Bottle Problem. | |
We have observed that calculus students frequently provided a strictly concave up graph in response to this question (Carlson, 1998 ; Carlson et al., 2002). When probed to explain their reasoning, a common type of justification was, "as the water is poured in it gets higher and higher on the bottle (MA2)." In contrast, other students who were starting to be able to construct an appropriate graph began coordinating the magnitude of changes in the height with changes in the volume (MA3). This is exemplified in the strategy of imagining pouring in one cup of water at a time and coordinating the resulting change in height based on how "spread out" that layer of water is.
Other students have demonstrated the ability to speak about the average rate of change locally for a specific interval of a function's domain (MA4) but were unable to explain how the rate changes over the domain of the function. Even when calculus students produced a graph that was correct, they commonly had difficulty explaining what was conveyed by the inflection point and why the graph was "smooth" (i.e., C1 rather than piecewise linear). Students frequently exhibited behaviors that gave the appearance of engaging in Mental Action 5 (e.g., construction of a smooth curve with the correct shape), however when prompted to explain their reasoning, they explained that they had relied on memorized facts to guide their constructions. They were relying on facts such as faster means steeper and slower means less steep, but they were unable to explain why this was true.
Engaging covariational reasoning through analysis of function situations
We offer the following suggestions for strengthening students' covariational reasoning abilities:
Concluding remarks
References
- Breidenbach, D., Dubinsky, E., Hawks, J., & Nichols, D. (1992). Development of the process conception of function. Educational Studies in Mathematics, 23, 247-285.
- Carlson, M., Jacobs, S., Coe, E., Larsen, S., & Hsu, E. (2002). Applying covariational reasoning while modeling dynamic events: A framework and a study. Journal for Research in Mathematics Education, 33(5), 352-378.
- Carlson, M., Oehrtman, M., & Engelke, N. (submitted). The development of an instrument to assess precalculus students' conceptual understandings: The Precalculus Concept Assessment Instrument.
- Carlson, M. P. (1998). A cross-sectional investigation of the development of the function concept. In A. H. Schoenfeld, J. Kaput, & E. Dubinsky (Eds.), Research in Collegiate Mathematics Education. III. CBMS Issues in Mathematics Education (pp. 114-162). Providence, RI: American Mathematical Society.
- Carlson, M. P. (1999). The mathematical behavior of six successful mathematics graduate students: Influences leading to mathematical success. Educational Studies in Mathematics, 40, 237-258.
- Carlson, M. P., Smith, N., & Persson, J. (2003). Developing and connecting calculus students' notions of rate of change and accumulation: The fundamental theorem of calculus. In N. A. Pateman, B. J. Dougherty, & J. T. Zilliox (Eds.), Proceedings of the 2003 Joint Meeting of PME and PMENA, Vol. 2 (pp. 165-172). Honolulu, HI: CRDG, College of Education, University of Hawai'i.
- College Entrance Examination Board. (1959). Program for college preparatory mathematics. New York: Commission on Mathematics.
- Cooney, T., & Wilson, M. (1996). Teachers' thinking about functions: Historical and research perspectives. In T. A. Romberg & E. Fennema (Eds.), Integrating research on the graphical representation of functions (pp. 131-158). Hillside, NJ: Lawrence Erlbaum.
- Cottrill, J., Dubinsky, E., Nichols, D., Schwingendorf, K., Thomas, K., & Vidakovic, D. (1996). Understanding the limit concept: Beginning with a coordinated process schema. Journal of Mathematical Behavior, 15(2), 167-192.
- Dubinsky, E. (1991). Reflective abstraction in advanced mathematical thinking. In D. Tall (Ed.), Advanced mathematical thinking (pp. 95-126). Boston: Kluwer Academic Publishers.
- Dubinsky, E., & Harel, G. (1992). The nature of the process conception of function. In G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy. MAA Notes, 25, 85-106.
- Dubinsky, E., Schwingendorf, K., & Mathews, D. M. (1994). Calculus, concepts, and computers. New York: McGraw-Hill Publishing.
- Hamley, H. R. (1934). The history of the function concept. In W. D. Reeve (Yearbook Ed.) & H. R. Hamley (Vol. Author), The ninth yearbook of the National Council of Teachers of Mathematics: Relational and functional thinking in mathematics (pp. 48-84). New York: Bureau of Publications, Teachers College, Columbia University.
- Hedrick, E. R. (1922). Functionality in the mathematical instruction in schools and colleges. The Mathematics Teacher, 15, 191-207.
- Hughes-Hallett, D., & Gleason, A. M. (1994). Calculus. New York: Wiley.
- Kaput, J. (1992). Patterns in students' formalization of quantitative patterns. In G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy. MAA Notes, 25. Washington D.C.: Mathematical Association of America.
- Kaput, J. (1994). Democratizing access to calculus: New routes to old roots. In A. H. Schoenfeld (Ed.), Mathematics and Cognitive Science (pp. 77-156). Washington, DC: Mathematical Association of America.
- Klein, F. (1883). Ueber den allgemeinen Functionbegriff und dessen Darstellung durch eine willknerliche Curve. Mathematischen Annalen, XXII, 249.
- Kleiner, I. (1989). Evolution of the function concept: A brief survey. The College Mathematics Journal, 20(4), 282-300.
- Monk, S. (1987). Students' understanding of functions in calculus courses. (Unpublished manuscript, University of Washington, Seattle, WA).
- Monk, S. (1992). Students' understanding of a function given by a physical model. In G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy (pp. 175-194), MAA Notes, 25. Washington, DC: Mathematical Association of America.
- Monk, S., & Nemirovsky, R. (1994). The case of Dan: Student construction of a functional situation through visual attributes. In E. Dubinsky, A. H. Schoenfeld, & J. Kaput (Eds.), Research in Collegiate Mathematics Education. I. CBMS Issues in Mathematics Education (pp. 139-168). Providence, RI: American Mathematical Society.
- National Council of Teachers of Mathematics. (1934). Relational and Function Thinking in Mathematics, 9. Reston, VA: National Council of Teachers of Mathematics.
- National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
- National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
- Nemirovsky, R. (1996). A functional approach to algebra: Two issues that emerge. In N. Bednarz, C. Kieran, & L. Lee (Eds.), Approaches to algebra: Perspectives for research and teaching (pp. 295-313). Boston: Kluwer Academic Publishers.
- Oehrtman, M. (2002). Collapsing dimensions, physical limitation, and other student metaphors for limit concepts: An instrumentalist investigation into calculus students' spontaneous reasoning (Doctoral dissertation, University of Texas, Austin, TX).
- Ostebee, A., & Zorn, P. (1997). Calculus from graphical, numerical, and symbolic points of view. New York: Houghton-Mifflin.
- Rasmussen, C. L. (2000). New directions in differential equations: A framework for interpreting students' understandings and difficulties. Journal of Mathematical Behavior, 20, 55-87.
- Schwarz, B. B., & Hershkowitz, R. (1999). Prototypes: Brakes or levers in learning the function concept? The role of computer tools. Journal for Research in Mathematics Education, 30(4), 362-389.
- Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on process and objects as different sides of the same coin. Educational Studies in Mathematics, 22, 1-36.
- Sierpinska, A. (1992). On understanding the notion of the concept of function. In G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy (pp. 25-58). MAA Notes, 25. Washington, D.C.: Mathematical Association of America.
- Tall, D. (1992). The transition to advanced mathematical thinking: Functions, limits, infinity and proof. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 495-511). New York: Macmillan.
- Thompson, P. W.(1994a). Images of rate and operational understanding of the fundamental theorem of calculus. Educational Studies in Mathematics, 26, 229-274.
- Thompson, P. W.(1994b). Students, functions, and the undergraduate curriculum. In E. Dubinsky, A. H. Schoenfeld, & J. Kaput (Eds.), Research in Collegiate Mathematics Education. I. CBMS Issues in Mathematics Education (pp. 21-44). Providence, RI: American Mathematical Society.
- Vinner, S. (1997). The pseudo-conceptual and the pseudo-analytical thought processes in mathematics learning. Educational Studies in Mathematics, 34, 97-129.
- Zandieh, M. J. (2000). A theoretical framework for analyzing student understanding of the concept of derivative. In E. Dubinsky, A. H. Schoenfeld, & J. Kaput (Eds.), Research in Collegiate Mathematics Education. IV. CBMS Issues in Mathematics Education (pp. 103-127). Providence, RI: American Mathematical Society.
Marilyn P. Carlson, Director, CRESMET
Center for Research on Education in Science,
Mathematics, Engineering and Technology
Arizona State University
Tempe, AZ 85287-1804
Email: marilyn.carlson@asu.edu
and
Michael Oehrtman
Department of Mathematics and Statistics
Arizona State University
Tempe, AZ 85287-1804
Email: oehrtman@math.asu.edu




