- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Research Sampler 7: Learning and Teaching Ordinary Differential Equations
by Chris Rasmussen and Karen Whitehead
Making Connections between Representations
What Lies Beneath Correct Answers?
Numerical Approximations and Graphical Predictions
Proofs of Graphical Predictions
The Cultural Status of Graphical Representations
Student Understanding of Systems and Second Order Differential Equations
Technology
The Differential Equations Classroom
To Sum Up
References
Advances in technology, together with an increased interest in dynamical systems, are influencing the nature of many first courses in ordinary differential equations (ODEs). In addition, there is an increased emphasis on nonlinear differential equations, systems of differential equations, and mathematical modeling, as well as on qualitative and numerical approaches that shed light on the behavior of solutions. Analytic techniques are still important, but they no longer tend to be the sole focus. As these new directions come into classrooms, research is beginning to illuminate aspects of learning and teaching ODEs that can inform ongoing curricular innovations.
Making Connections between Representations
The interplay between algebraic, graphic, and numeric representations and the contextual situations that particular equations are intended to model is a common theme in reform efforts. Examples of problems of these types can be found in a Special Issue of the College Mathematics Journal [see West, 1994] and the Mathematical Association of America Notes #50 [see Kallaher, 1999]. Common amongst these is a need for students to move flexibly between algebraic, graphical, and numerical representations, to make interpretations from the various representations of situations being modeled, and to make warranted predictions about the long-term behavior of solutions. Are students successful on these types of problems â?? why or why not? Research is beginning to document students' accomplishments and difficulties, as well as providing theories about their possible cognitive and instructional origins.
In a French study aimed at exploring the teaching of qualitative solutions, Michèle Artigue conducted a three-year project with first-year students at the University of Lille I. Approximately 100 students per year received nearly 35 hours of instruction on first-order differential equations. Students attended common lecture sessions with smaller exercise sessions using computers. As evidenced by their lab reports and examinations, early on students were able to successfully complete tasks where information was given simultaneously in two settings and the problem to be solved required interpretation between the two settings. For example, one interpretation task asked students to find and justify the correct match between seven different differential equations and corresponding graphs of solution curves. With little or no intervention from the instructor, these students were successful because they were able to employ a variety of familiar criteria for determining and checking their answers. These criteria included connections between the sign of f (where dy/dx = f(x, y)) and properties of monotonicity for solution curves, zeros of f and horizontal slope, infinite limit of f and vertical slope, the value of f at a particular point and the slope of a solution curve at that point, and recognizing particular solutions associated with straight lines in the graphic setting and checking them in the algebraic setting. We would hope all students are familiar with these criteria from calculus, and thus, that such criteria can serve as a basis for further study of differential equations. [see Artigue (1992)]
What Lies Beneath Correct Answers?
One of the tasks required students to determine, with reasons, the appropriate match between eight differential equations and four slope fields (four of the differential equations did not have a matching slope field). Although all students were generally successful on this task (using many of the same criteria outlined by Artigue), Rasmussen found that behind students' correct answers there often lay an incorrect conception of equilibrium solution. In particular, three of the six students, at various points in their solution processes, conceptualized equilibrium solutions as existing whenever the differential equation is zero. While this is true for autonomous differential equations, it is not true in general. For example, when dealing with the equations dy/dt = y![]() t and dy/dt = t + 1, students tended to reason that y = t and t =
t and dy/dt = t + 1, students tended to reason that y = t and t = ![]() 1 were equilibrium solutions, respectively, and they used this to guide their work on the matching task. If we view such errors as making sense to the student, how might we account for this overgeneralization? One explanation involves the difficulty of conceptualizing a solution as a function that satisfies the differential equation. In previous math courses, students were accustomed to thinking of a solution as a number or numbers, but in differential equations, solutions are functions. Thus the letter y in a differential equation is meant to represent an unknown function, as well as being a variable in the differential equation itself. Moreover, students often associate the derivative with the slope of the tangent line at a point, which, when combined with our everyday use of the term equilibrium as balance point, tends to result in students considering equilibrium solutions as points where the derivative is zero, rather than as constant functions that satisfy the differential equation. [see Rasmussen (2001)]
1 were equilibrium solutions, respectively, and they used this to guide their work on the matching task. If we view such errors as making sense to the student, how might we account for this overgeneralization? One explanation involves the difficulty of conceptualizing a solution as a function that satisfies the differential equation. In previous math courses, students were accustomed to thinking of a solution as a number or numbers, but in differential equations, solutions are functions. Thus the letter y in a differential equation is meant to represent an unknown function, as well as being a variable in the differential equation itself. Moreover, students often associate the derivative with the slope of the tangent line at a point, which, when combined with our everyday use of the term equilibrium as balance point, tends to result in students considering equilibrium solutions as points where the derivative is zero, rather than as constant functions that satisfy the differential equation. [see Rasmussen (2001)]
Michelle Zandieh and Michael McDonald also studied students' underlying understanding of solutions and equilibrium solutions. They interviewed a total of 23 students from two separate reform-oriented differential equations classes, one at a large state university in the southwest and one at a small liberal arts college on the west coast. In addition to asking students open-ended questions such as, "What is a differential equation?" and "What is a solution to a differential equation?", they posed several tasks for students to solve. One of the tasks was the same matching task used by Rasmussen and another asked students to draw representative solutions on a given slope field for dy/dt = y + 1. Much like previous research findings, 7 of the 23 students overgeneralized the notion of equilibrium solution to include all values for which dy/dt is zero. When asked to draw representative solution functions, 3 of the 23 students failed to sketch the equilibrium solution y(t) = ![]() 1. Mathematically, we would expect students' notion of equilibrium solution to be a subset of their notion of solution, but for these students this did not appear to be the case. Consistent with Rasmussen's findings, these results underscore an important conceptual difficulty that may lie beneath many correct answers. [see Zandieh & McDonald (1999)]
1. Mathematically, we would expect students' notion of equilibrium solution to be a subset of their notion of solution, but for these students this did not appear to be the case. Consistent with Rasmussen's findings, these results underscore an important conceptual difficulty that may lie beneath many correct answers. [see Zandieh & McDonald (1999)]
In another task Rasmussen provided students with the autonomous differential equation dN/dt = ![]() 4N(1
4N(1![]() N/3) (1
N/3) (1![]() N/6) and the corresponding graph of dN/dt vs. N. He asked the following three questions: (a) What are the equilibrium solutions? (b) Which of the equilibrium solutions are stable and which are unstable? (c) What is the limiting population for N(0) = 2, N(0) = 3, N(0) = 4, and N(0) = 7? All six interview subjects figured out the correct answers to parts (a) and (b) but four of the six students were unable to address part (c). This was particularly surprising because the typical student approach to this problem was to figure out the first two parts by creating a sketch like that in Figure 1.
N/6) and the corresponding graph of dN/dt vs. N. He asked the following three questions: (a) What are the equilibrium solutions? (b) Which of the equilibrium solutions are stable and which are unstable? (c) What is the limiting population for N(0) = 2, N(0) = 3, N(0) = 4, and N(0) = 7? All six interview subjects figured out the correct answers to parts (a) and (b) but four of the six students were unable to address part (c). This was particularly surprising because the typical student approach to this problem was to figure out the first two parts by creating a sketch like that in Figure 1.
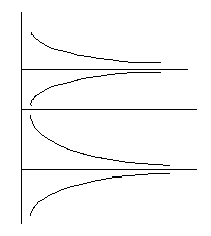
Why would students be able to do parts (a) and (b), but fail to "see" the connection between their sketches and the long-term behavior for various initial populations? This question is especially intriguing because these students had just created for themselves what is from our perspective a sketch like that in Figure 1 of various solution functions. During the interviews, the answer to this question became quite clear. Students did not view the sketch they had just created as a plot of the functions that solve the differential equation. In the words of one student, his sketch was "just a test for stability." These students had learned a graphical approach for determining stability where the graphs they created did not carry the intended conceptual meaning. [see Rasmussen (2001)]
Research findings focusing on student understanding in courses taking new directions in ODEs indicate that graphical and qualitative approaches do not automatically translate into conceptual understanding. In a traditional course, a typical complaint is that students often learn a series of analytic techniques without understanding important connections and conceptual meanings. Care must be taken or else students are likely to supplement mindless symbolic manipulation with mindless graphical manipulation. Of course, how a student thinks and reasons is as much a reflection of his or her individual cognitive development as it is a reflection of the mathematics classroom. For example, if students are not routinely expected to explain and mathematically defend their conclusions, it is more likely that they will learn to proceduralize various graphical and qualitative approaches in ways that are disconnected from other aspects of the problem.
Numerical Approximations and Graphical Predictions
Half of the six students incorrectly reasoned that solutions starting off in the upper left-hand region would tend to zero as x approaches infinity. Despite evidence to the contrary, these students demonstrated strong intuitive notions that asymptotic behavior would prevail. For example, one student figured out that all the slopes in the first quadrant just above the x-axis would have a positive slope, but rejected this as irrelevant to the long-term behavior of solutions that initially approached the positive x-axis. These students are in good company. As James Gleick described in his book, Chaos: The Making of a New Science, the famous mathematician Stephen Smale once proposed that practically all dynamical systems tend to settle into behavior that is not too strange. For students in a first course in ODEs, solutions that hint at asymptotic behavior, but then change course, appear too strange to be believable. [see Rasmussen (2001)]
Proofs of Graphical Predictions
Since graphical predictions are playing an increasingly prominent role in reform-oriented approaches to ODEs (see for example, Blanchard, Devaney, and Hall, 2002; Borrelli and Coleman, 1998; Diacu, 2000; Kostelich and Armbruster, 1997), it makes sense to explore the extent to which students are able to create geometric proofs. Artigue's work specifically examined this issue; she reported on students' work on three types of tasks â?? prove that a solution intersects a given curve; prove that it cannot intersect a given curve; and prove that it has an asymptote or rule out the possibility of such an infinite branch. She found that students had great difficulties generating these proofs. She attributes this to two causes. First, students had not been exposed to the delicate tools that they needed to use in qualitative proofs in the graphical setting. For example, the helpful ideas of fence, funnel, and area had not been introduced to students because, as Artigue suggests, mathematics professors have been slow to accept the graphical setting as a place for proof. Second, many students have strong monotonic conceptions that interfere with their proof efforts. For example, students had an intuitive belief in the following false statement: If f(x) has a finite limit when x tends towards infinity, its derivative f '(x) tends toward zero. Yet another reason for students' difficulty was that moving from predictions about how a solution might look to actually proving these statements requires the use of elementary analysis. [see Artigue (1992)]
A different approach to proofs involves emphasizing argumentation as a routine part of everyday classroom discussions. In a multi-year project at a mid-sized university in the Midwest, researchers2 are studying student learning in a first course in ODEs as it occurs in classrooms over the course of an entire semester. An interesting example from this research related to proof involves the arguments students developed to justify that two solutions to a logistic growth differential equation with different initial conditions would never touch. Although these students had not yet studied the uniqueness theorem, they argued that since graphs of solutions to autonomous different equations were shifts of each other along the t-axis, there would never be a point in time when the solutions intersected each other. For another example of arguments involving short chains of deductive reasoning, consider the following question that students in this project asked and answered: Is it possible for a graph of a solution to an autonomous differential equation to oscillate? The typical argument these students developed to reject this possibility was to argue that since the slopes in a slope field for an autonomous differential equation would have to be the same "all the way across" the slope field, a graph of a solution would not oscillate because if it did, there would be a value for y where the slope would be both positive and negative. For students like those in this class who have little to no experience in developing mathematical arguments to support or refute claims, significant progress in their ability to create and defend short deductive chains of reasoning was observed. This progress was due in large part to the explicit attention paid to classroom norms pertaining to explanation and justification. These social aspects of the mathematics classroom are reviewed in the final section. [see Stephan & Rasmussen (2002)]
The Cultural Status of Graphical Representations
Students typically enter a first course in differential equations with a significant amount of previous experience in mathematics courses where answers more often than not involved numbers and equations â?? objects that live in the analytic, or symbolic, setting. This may well serve as a stumbling block to using the graphical setting as a way to understand solutions of differential equations and to qualitatively understand families of solutions. As a result, students may implicitly believe that graphical solutions are less than desirable. Samer Habre pursued this line of inquiry in a study that investigated students' use of visual representations of solutions to ODEs. Students from a third semester four credit calculus class at a large northeastern university where the first half of the course covered multivariable calculus and the second half was devoted to differential equations were his subjects. Data included classroom and lab observations, students' exams and assignments, and a 45-minute interview with nine of the students in the class. One of the questions in the interview was, "What comes to your mind when you are asked to solve an ODE?" The initial response from all nine subjects indicated that the students thought of an analytic solution. Their dominant notion of what constitutes a solution remained in the analytic realm even though a significant amount of class involved learning qualitative methods that relied heavily on technology to look at vector fields and other graphical representations. Habre's research lends further support to the claim that students' concepts about solutions as analytic are resistant to change and that moving to the graphical setting to understand ODEs is extremely difficult. Students' reluctance to value graphical solutions equally with analytic solutions is likely a result of the mathematical culture that they have experienced in many of their previous mathematics classrooms. [see Artigue (1992); Habre (2000)]
Student Understanding of Systems and Second Order Differential Equations
In addition to research on the learning and teaching of first order ODEs, researchers are beginning to examine students' understandings of systems and second order differential equations. In one study, Maria Trigeuros investigated student learning of systems of differential equations in two ODE classes at a small private university in Mexico. Three individual task-based interviews were conducted with nine students in each class. Her analysis of the interviews reveals that some students had problems interpreting the meaning of equilibrium solution (which was an issue for students in single ODEs as well), interpreting the meaning of a point in phase space, and seeing the dependence of time in the phase space. Students in her study also showed a tendency to focus on just part of the information provided by phase portraits. Only a few students analyzed long-term behavior of solutions in relation to equilibrium solutions. [see Trigueros (2000)]
In Rasmussen's study, students discussed a previously completed Mathematica assignment where they had generated and interpreted graphs of the angular position (in radians) versus time for the linear and non-linear differential equations similar to those shown in Figure 3. Each plot in Figure 3 shows a different set of initial conditions for the solutions to the undamped linear model, ![]() '' +
'' + ![]() = 0 and to the undamped nonlinear model,
= 0 and to the undamped nonlinear model, ![]() '' + sin
'' + sin ![]() = 0. Graphs of solutions to the nonlinear model are indicated with NL.
= 0. Graphs of solutions to the nonlinear model are indicated with NL.
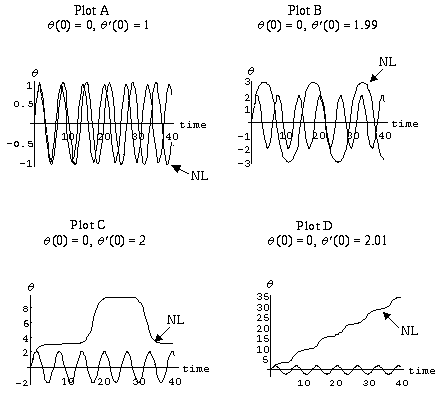
As might be expected, students experienced the most difficulty interpreting the graphs in Plots C and D. Students tended to interpret the graph as a literal picture of the situation. For example, one student said that the graph of the solution to the nonlinear model in Plot C indicates that "it starts increasing and remains at a constant distance from, whatever, and then it would start increasing again spontaneously, plateau again and then start increasing." He also acknowledged that he had never seen a pendulum do something like that, but was unable to interpret the plot otherwise. In Plot D, this same student explained that the graph of the solution to the nonlinear model shows the pendulum "increasing and increasing and this thing wouldn't be able to hold it and it would just fly off." [see Rasmussen (2001)]
The studies by Trigueros and Rasmussen suggest that developers of both curriculum and instruction need to be cautious about what is assumed will be obvious to students when dealing with rich and complex graphical representations. Perhaps further and deeper classroom conversations surrounding the interpretation of such representations might help minimize the types of student difficulties highlighted in these studies.
Technology
One study conducted by Thomas Klein concerned how the use of a computer algebra system as a demonstration tool affects achievement in solving differential equations. Klein investigated four sections of ODE classes consisting of 110 students at a large private university in the southeast. In two classes, the instructor used a computer algebra system (CAS) as an in-class teacher-led demonstration tool and students were given access to the same system out of class. In the other two classes, no CAS was used. A common posttest was given to all the classes, along with questionnaires and interviews with students in the CAS classes. In comparing the classes, Klein found no significant difference in students' ability to analytically solve ODEs. This result is perhaps not surprising since the power a CAS offers does not relate well to the development of paper and pencil skills necessary to analytically solve ODEs. However, students in the CAS classes did show more positive attitudes about the use of computers in mathematics. [see Klein (1993)]
In the study conducted by Rasmussen at the large mid-Atlantic university, students worked on CAS labs outside of class time and only rarely did class discussion focus on interpretations or analysis of their labwork. As documented by interviews and surveys, students viewed these CAS labs as unrelated to what they saw as the main ideas of the course and they did not think that the work they put into the labs furthered their understandings of important ideas or methods, which was contrary to the instructor's goals of the course. However, when technology is integrated into the course, there is some evidence that this does help promote better understandings of various graphical representations. For example, in Habre's study students used computer modules designed for specific course goals of the course and intended to introduce students to specific concepts. Although this was not the focus of his research, some of Habre's interview data suggests that these modules might have been helpful to students in their development of mathematics in the graphical setting. For example, when given a vector field for the system of ODEs x'(t) = ![]() x + 4y, y'(t) =
x + 4y, y'(t) = ![]() 3x
3x![]() y, all the students he interviewed were able to draw an appropriate trajectory in the xy-plane and to draw reasonable x(t) and y(t) graphs corresponding to this trajectory. Some students, however, faced difficulties in drawing the 3D-parametric curve. Habre suggests that the role of such computer modules in student learning warrants further study. [see Rasmussen (1997); Habre (2000)]
y, all the students he interviewed were able to draw an appropriate trajectory in the xy-plane and to draw reasonable x(t) and y(t) graphs corresponding to this trajectory. Some students, however, faced difficulties in drawing the 3D-parametric curve. Habre suggests that the role of such computer modules in student learning warrants further study. [see Rasmussen (1997); Habre (2000)]
What this limited research does indicate is that we need to be deliberate in how and why we decide to implement technology in the classroom. It shows that students' visual understanding of phase portraits, slope fields, and solutions of differential equations is an area where we might consider integrating technology into students' experiences in the classroom. Using a computer algebra system as a separate lab component or only as a demonstration tool seems less likely to achieve the intended learning goals.
The Differential Equations Classroom
In two different semester long research studies conducted at a midwestern university, Chris Rasmussen, Erna Yackel, Michelle Stephan, and Karen King investigated the feasibility of adapting research-based approaches to instructional design and teaching that have been effective at promoting student learning at the school level (in particular the theory of Realistic Mathematics Education being developed at the Freudenthal Institute in The Netherlands). The project classes involved differential equations students majoring in mathematics, science, or engineering. All classes were video-taped and individual interviews were conducted with a majority of the students at various points throughout the semester. The data consisted of classroom video-recordings, field notes, copies of student work, and video-recorded individual student interviews. In this section, we highlight the work based on these project classes. [see Rasmussen & King (2000); Yackel, Rasmussen, & King (2000); Rasmussen, Yackel, & King (in press)]
Findings include the significant role of explanation and justification as a normal part of classroom discussion. The following classroom features, critical to the success of the project in terms of student learning, were initiated by the instructor and sustained throughout the semester: Students routinely explained their thinking and reasoning (versus just providing answers), listened to and tried to make sense of other students' thinking, indicated agreement or disagreement with other students' thinking, and responded to other students' challenges and questions. Such aspects of classroom social interactions involving explanation and justification that become routine are referred to as social norms. The initiation and maintenance of such norms was a challenge because students in the project classes were used to and expected traditional patterns of interaction where the instructor talked and the students listened.
Given that many undergraduate students are not used to explaining their reasoning and making sense of other students' thinking, a pervasive and important question is: How can instructors (1) initiate a shift in social norms, and (2) sustain these norms over time? The studies conducted by Rasmussen and colleagues offer useful responses. For example, in the semester-long classroom studies described, the instructor devoted explicit attention to initiating the social norms described above. During an approximately twenty-minute whole class discussion on the second day of class, the instructor led a whole discussion where he offered no mathematical explanation himself. Rather, he strove to initiate new social norms by inviting students to discuss their thinking and reasoning through remarks and questions such as:
- Tell us how you thought about it. That's what we're interested in.
- What do some of the rest of you think about what Jason just said?
- Did anyone think about that in a different way?
- That's a good question. Let's put that question out to the rest of the class. What do the rest of you think about it?
- Tell us why you are thinking that.
- I'm not sure that everyone heard what you were saying. Say it again please.
- Say a bit more about that.
Social norms are not rules set out in advance on a syllabus. Although being explicit about expectations can be useful, such explicit statements are insufficient. Norms are regularities in the ways individuals interact. As such, an instructor alone cannot establish them. They are constituted and sustained through participation and interaction over time. As students and the instructor act in ways that are consistent with new expectations regarding explanation and justification, they contribute to their ongoing constitution.
Another point, which is illustrated in two case studies at two different U.S. universities, is that every class, from the most traditional to the most reform-oriented, has social norms that are operative for that particular class. It is not the presence or absence of social norms that differentiates one class from one another. Rather, it is the nature of the norms that differ from class to class. Of course the social norms pertaining to explanation and justification might apply to a history class or an English literature class, as well as a mathematics class. The term sociomathematical norm refers to the fact that the subject being learned is mathematics. The expectation that one is to give an explanation is a social norm, but what is considered to be an elegant solution, a different solution, an efficient solution, or an acceptable mathematical explanation are sociomathematical norms. For example, when students develop predictions and explanations about the future of say, the population of fish in a lake, it is imperative that these explanations move beyond conclusions based solely on contextual reasons (e.g., the fish are going to run out of food, so their numbers are going to decrease) to include reasons that rely on an interpretation of the mathematical idea of rate grounded in the differential equation. Fostering a classroom learning environment that promotes the types of explanations valued by the mathematics community is a process that evolves over time as students and instructor interact in the classroom setting. If instructors are interested in promoting a classroom environment where students routinely give and evaluate mathematical arguments, explicit attention to the processes by which norms are constituted is a first step.
Finally, this research team documented how these evolving norms fostered a shift in student beliefs about their role as learners, about their instructor's role, and about the general nature of mathematical activity. These beliefs shifted from seeing their role as passive absorbers of information to active participants in knowledge creation. When the classroom is viewed as a dynamic system that includes the way in which students participate in mathematical learning, we can account not only for how student beliefs evolve and develop, we can also promote student beliefs about mathematics more compatible with the discipline itself. [see Yackel & Rasmussen (in press)]
To Sum Up
The teaching and learning of differential equations is heading in new directions due in part to an increasing interest in dynamical systems and a broad interest in improving mathematics learning and teaching across K-16. The use of technology and the "rule of four" (concepts and methods should be approached graphically, numerically, analytically, and descriptively) are a springboard for looking at new ways for students to understand central ideas and methods in differential equations. In addition to new pedagogical strategies, research into students' thinking and reasoning is yielding new insights into ways to create and sustain learning environments where students can gain deep understandings of mathematical concepts and methods.
References
- Artigue, M. (1992). Cognitive difficulties and teaching practices. In G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy (pp. 109-132). Washington, DC: The Mathematical Association of America.
- Blanchard, P., Devaney, R., & Hall, R. (2002). Differential equations. Pacific Grove, CA: Brooks/Cole.
- Borrelli, R., & Coleman, C. (1998). Differential equations: A modeling perspective. New York: Wiley.
- Diacu, F. (2000). An introduction to differential equations: Order and chaos. New York: W. H. Freeman.
- Gleick, J. (1987). Chaos: Making a new science. New York: Penguin Books.
- Habre, S. (2000). Exploring students' strategies to solve ordinary differential equations in a reformed setting. Journal of Mathematical Behavior, 18, 455-472.
- Kallaher, M. J. (Ed.) (1999). Revolutions in differential equations: Exploring ODEs with modern technology. Washington, DC: The Mathematical Association of America.
- Klein, T. J. (1993). A comparative study on the effectiveness of differential equations instruction with and without a computer algebra system. Dissertation Abstracts International, 54(11), (University Microfilms No. AAC94-12432).
- Kostelich, E., & Armbruster, D. (1997). Introductory differential equations: >From linearity to chaos. Reading, MA: Addison-Wesley.
- Rasmussen, C. (1997). Qualitative and numerical methods for analyzing differential equations: A case study of students' understandings and difficulties. Unpublished doctoral dissertation, University of Maryland, College Park.
- Rasmussen, C. (2001). New directions in differential equations: A framework for interpreting students' understandings and difficulties. Journal of Mathematical Behavior, 20, 55-87.
- Rasmussen, C. & King, K. (2000). Locating starting points in differential equations: A realistic mathematics approach. International Journal of Mathematical Education in Science and Technology, 31, 161-172.
- Rasmussen, C., Yackel, E., & King, K. (in press). Social and sociomathematical norms in the mathematics classroom. In R. Charles (Ed.), Teaching mathematics through problem solving: It's about learning mathematics. Reston, VA: National Council of Teachers of Mathematics.
- Stephan, M. & Rasmussen, C. (2002). Classroom mathematical practices in differential equations. Journal of Mathematical Behavior, 21, 459-490.
- Trigueros, M. (2000). Students' conceptions of solution curves and equilibrium in systems of differential equations. In Fernandez, M. L. (Ed.), Proceedings of the 22nd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 93-97). Columbus, OH: ERIC.
- West, B. (Ed.) (1994). Special issue on differential equations [Special issue]. The College Mathematics Journal, 25(5).
- Yackel, E. & Rasmussen, C. (in press). Beliefs and norms in the mathematics classroom. In G. Toerner, E. Pehkonen, & G. Leder (Eds.). Mathematical beliefs and implications for teaching and learning. Dordrecht, The Netherlands: Kluwer.
- Yackel, E., Rasmussen, C., & King, K. (2000). Social and sociomathematical norms in an advanced undergraduate mathematics course. Journal of Mathematical Behavior, 19, 275-287.
- Zandieh, M. & McDonald, M. (1999). Student understanding of equilibrium solution in differential equations. In F. Hitt & M. Santos (Eds.), Proceedings of the 21st Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 253-258). Columbus, OH: ERIC.
2 The research in students' learning of differential equations began in 1998 with Chris Rasmussen, Erna Yackel, and Karen King. Since that time the project team has expanded to include Michelle Stephan, Karen Whitehead, Michael Keynes, and Wei Ruan. At the time of this review, these researchers were collaborating with Karen Marrongelle, Oh Nam Kwon in South Korea, and Mark Burtch.
Chris Rasmussen
Department of Mathematics, Computer Science & Statistics
2200 169th Street
Purdue University Calumet
Hammond, IN 46323
Email: raz@calumet.purdue.edu
Karen Whitehead
Department of Math and Computer Science
Valparaiso University
Valparaiso Indiana
Email: Karen.Whitehead@valpo.edu





