- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Virginia State University
Virginia State University
Title: (i) A Pursuit-Evasion Game on Graphs, (ii) Wavelet shrinkage
Directors: Dawit Haile
Email: dhaile@vsu.edu
Dates of Program: May 16 ? June 30, 2011
Summary:
(i) In a pursuit evasion game, the pursuer tries to capture the evader while the evader tries to prevent this capture. So, the objective of the game is to devise a strategy to guide one or a group of pursuers to catch one or a group of moving evaders. Because of its extensive applications, such as searching buildings for intruders, traffic control, military strategy, and surgical operation, a lot of research has been done on this problem. In this activity, we will study a special pursuit evasion game on graphs.
Let G be a connected graph. We consider two players, each independently select a vertex of G. The first player then pays the second player an amount equal to the distance between the vertices chosen. A strategy for the game is defined as a vector x = (x(v) : v in G) where x(v) denotes the probability that the player chooses vertex v. The value of G, v(G), is defined as  or
or 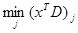 , where D = D(G) is the distance matrix of G. Here the distance matrix D = D(G) serves as a payoff matrix for this pursuit evasion game on G. This portion of the summer activity involves investigation of v(G) for different classes of graphs.
, where D = D(G) is the distance matrix of G. Here the distance matrix D = D(G) serves as a payoff matrix for this pursuit evasion game on G. This portion of the summer activity involves investigation of v(G) for different classes of graphs.
(ii) Wavelets are collections of functions that can be used to decompose signals into various frequency components at an appropriate resolution for a range of spatial scales. The idea of decomposing a signal into frequency components has been heavily exploited with the use of Fourier decompositions which use sines and cosines as their basis functions. The clear advantage of wavelets over traditional Fourier methods is that they are localized in both space or time and frequency. Wavelet Transforms provide powerful techniques of converting continuous analog data sets to a digital framework. One particular important application is the ability to compress data to allow for more compact and efficient storage. The students who had participated in the summer 2009 project used one such transformation ? the Haar Wavelet Transform (HWT) and studied its applications in image compression and recovery by giving particular emphasis to the storage of recovery of various images. They also explored how to achieve high compression ratio in images using 2D-HWT by applying different compression thresholds for the wavelet coefficients. This summer we will examine various methods of Wavelet Shrinkage as application to denoising. Several applications of denoising in medical signal image analysis (ECG, CT, MRI, etc.) and data mining will be discussed. Comparisons of various shrinkage methods (such as VisuShrink, SureShrink and Bayes) will be studied.
Student Researchers Supported by MAA:
- Shakiyla Huggins
- Jonathan McMillon
- Marcus Oliver
- Charlena Toliver
- Janelle Williams
Program Contacts:
Bill Hawkins
MAA SUMMA
bhawkins@maa.org
202-319-8473
Michael Pearson
MAA Programs & Services
pearson@maa.org
202-319-8470




