- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Calculus for the Forgetful

Publisher:
MagiMath Publishing
Publication Date:
2007
Number of Pages:
150
Format:
Paperback
Price:
19.95
ISBN:
9780979519901
Category:
Textbook
[Reviewed by , on ]
Kenneth A. Ross
08/13/2007
This is one of the shortest calculus books available: it can be read in a couple of days if needed. Yet it provides a concise treatment of single variable calculus, along with many exercises and more than 130 examples. Informal, intuitive language is used to present the theory in a nutshell. It is very valuable for students to have a general understanding of why various statements are true. This book helps them reach this goal. Some topics are omitted for the sake of brevity, and the book is focused on the core ideas, with just a few digressions here and there.
“Calculus for the Forgetful” is an ideal complement to any of the comprehensive calculus texts. It can be used by students currently taking a calculus course, as well as by those who would like to review and organize their knowledge. Those who plan to take more advanced mathematics courses or are preparing for standardized tests will also benefit from it. The book is small enough to be carried around to other classes in which calculus is used.
The preceding two paragraphs are taken from the book jacket, and they summarize well the goals of this small book. Indeed, this book weighs 8 ounces (227 g) and yet has over 150 examples. I believe that the author has very successfully accomplished his goals and that the book is ideally suited for readers needing a calculus refresher.
For the key results, the author briefly, and often cleverly, explains the ideas, but it must be understood by the mathematically-inclined reader that details will be missing and subtleties overlooked. But what is given helps explain why a result is true and often helps remember the result. The author is brave to take this approach, and I found only one misstatement that I felt needs modifying; see below.
Some especially good (partial) explanations occur when presenting the product rule, l’Hôpital’s rule, and the substitution rule for integration. For example, the product rule is explained by analyzing the rate of change of the area of a rectangle A(t) with sides f(t) and g(t). He then provides a formal proof that would fit his motivation even better if he used the formula
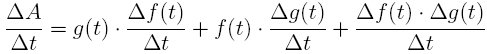
I also enjoyed his introductory comments about integration with some good news, some bad news and some warnings! Beginning instructors of calculus will benefit from some of the well-motivated discussions in this book.
The one misstatement that bothered me is on page 17: “The positive value of the derivative means that the function itself is increasing, at least in the immediate vicinity of the point in question.” This is “usually” true, but not always. If it were always true, the Mean Value Theorem wouldn’t be needed to prove that if the derivative is positive on an interval, then the function f is increasing on that interval. This correction and some other minor corrections are listed in the author’s errata at http://www.magimath.com/CFFErrata.pdf.
As short as this book is, not all readers will read all of it. Those using it to review for standardized exams may find all of it useful. People who mostly need a good overview and intuition, though, are less likely to need, for example, sections 6.3 and 6.4 on techniques of integration. All in all, this is a fine addition to the calculus literature that should help many students and ex-students of calculus as well as beginning instructors of calculus.
Kenneth A. Ross (ross@math.uoregon.edu) taught at the University of Oregon from 1965 to 2000. He was President of the MAA during 1995-1996. Before that he served as AMS Associate Secretary, MAA Secretary, and MAA Associate Secretary. His research area of interest was commutative harmonic analysis, especially where it has a probabilistic flavor. He is the author of the book Elementary Analysis: The Theory of Calculus (1980, now in 14th printing), co-author of Discrete Mathematics (with Charles R.B. Wright, 2003, fifth edition), and, as Ken Ross, the author of A Mathematician at the Ballpark: Odds and Probabilities for Baseball Fans (2004).
1. Preliminary Concepts and Facts
2. Limits and Derivatives, the Concept
3. How to Find Derivatives
4. Some Applications of Derivatives
5. The Integral and its Properties
6. Methods of Integration
7. Selected Applications of the Integral
8. Infinite Sequences and Series
A. Review of Terms
B. Selected Proofs
C. Answers and hints to selected problems
D. Concepts and ideas not to be forgotten
Bibliography
Index
Sample pages, including a more detailed table of contents, can be found on the MagiMath web site.
- Log in to post comments




